激波誘導火焰變形、混合和燃燒的數值研究＊

朱躍進，董 剛，2，劉怡昕，范寶春，蔣 華

（1.南京理工大學瞬態物理重點實驗室，江蘇 南京210094；2.北京理工大學爆炸科學與技術國家重點實驗室，北京100081）

激波掠過預混火焰界面時，會誘導界面出現大尺度的Richtmyer－Meshkov（RM）不穩定和小尺度的Kelvin－Helmholtz（KH）不穩定，導致火焰界面發生變形，進而強化未燃氣與可燃氣的混合，并促進流場湍流化，引起燃燒放熱的增強。這一系列復雜的物理化學現象不僅會發生在某些自然現象（如超新星爆炸［1］等）中，而且還常常在超燃推進［2］、工業爆炸災害［3］等出現，因此有關激波誘導的火焰變形、混合和燃燒等特性的研究具有重要意義。

作為可壓縮化學反應流動中的一個基本問題，平面激波與火焰界面相互作用的研究得到了一定程度的開展。G.H.Markstein［4］首先開展了激波管內激波與火焰相互作用的實驗研究，顯示了火焰在弱激波及反射激波作用下的變形過程；V.T.Ton等［5］考察了化學反應對激波－射流火焰相互作用的影響，由于采用的激波馬赫數較小（Ma＝1.093），因而化學反應對火焰的影響并不大，火焰變形過程與惰性介質密度界面的變形過程類似；Y.Ju等［6］研究了不同入射激波強度對火焰變形的影響規律，結果顯示，激波強度的增加可顯著增加火焰界面的長度，使已燃氣和未燃氣接觸面增加，進而提高火焰的燃燒速率。A.M.Khokhlov等［7］采用帶化學反應的二維Navier－Stokes（NS）方程對入射激波與火焰的單次作用過程進行了數值研究，結果表明，RM不穩定是火焰變形的主要機制，變形后的火焰與周圍未燃氣的混合強化，其表面積增加，燃燒速率和放熱速率均有所提高。但他們也指出，入射激波與火焰的單次作用對火焰變形和混合、燃燒的強化是有限的。接著，他們采用相同的數值方法，進一步研究了激波管中入射激波及其在管道封閉端形成的反射激波與火焰多次作用的過程，計算發現層流火焰在激波的多次擾動下高度變形并形成湍流火焰，其火焰表面積明顯增加，燃燒放熱率顯著提高［8－9］，這個結果也得到了G.O.Thomas等的實驗證實［10］。G.Dong等［11］采用數值模擬方法分析了激波與火焰作用過程，考察了不同化學反應機理和網格尺寸對結果的影響。

由上述可以看出，激波與火焰界面的相互作用涉及火焰變形、混合與燃燒放熱等基本過程，它們之間存在相互影響。一般認為，激波誘導火焰引起的變形可以強化火焰兩側未燃氣與已燃氣的混合，從而促進燃燒。但是，目前不僅缺少混合和燃燒兩者之間關系的詳細描述，而且也缺乏對兩者關系的進一步認識。為了深入細致闡明激波誘導的火焰變形以及由此帶來的混合與燃燒之間的相互作用關系，同時避免三維計算帶來過大的計算量，本文中，對平面入射激波及其反射激波誘導球形火焰變形的現象進行了二維數值研究，通過定義有效的量化參數，分析流場中變形火焰的演變過程、火焰幾何量變化、燃燒放熱規律、混合與燃燒的作用關系等特性，以深入理解激波與火焰作用的基本現象和規律。

1 數理模型與實驗驗證

1.1 數理模型

為描述激波與火焰的相互作用過程，采用的二維帶化學反應的Navier－Stokes方程表示：

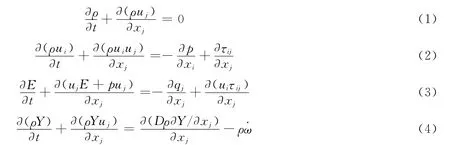
式中：ρ為密度，ui為i方向速度（i＝1，2），p為壓力，τij為黏性應力張量，E 為體積總能量，E＝p／（γ－1）＋0.5ρ∑2i＝1u2i＋ρqY，p為壓力，γ 為比熱比，q為質量總化學能，Y 為反應物質量分數，qj為熱通量，qj＝－k?T／?xj，ω為化學反應速率，熱擴散率k、擴散系數D、運動黏度ν可表示如下［3］：

式中：ν0、D0、k0是常數，T 為溫度，n＝0.7，本文中設路易斯數、普朗特數和施密特數均為1，則可選取常數ν0＝D0＝k0＝3.2×10－7kg／（s·m·K0.7）。

控制方程（1）～（4）采用分裂算法求解。空間導數項的黏性部分采用二階空間中心差分計算，無黏部分采用高精度五點TVD格式［12］計算，時間推進過程采用二階Runge－Kutta方法求解。

采用單步化學反應模型描述體系中的燃燒過程，化學反應熱力學和動力學參數的選取見文獻［13］，反應速率可表達為：

式中：A 為指前因子，取A＝1.2×108m3／（kg·s），Ea為活化能，取Ea／RT0＝38.2，T0代表預混氣的初始溫度，R為通用氣體常數。預混氣的化學反應質量放熱量q和比熱比γ分別取qM／RT0＝39.76和γ＝1.258，其中M為預混氣的分子量，這組參數能同時反映火焰燃燒和爆轟的熱力學特性［13］。

圖1 計算區域和初始流場Fig.1 Computational domain and initial flow field

1.2 初始及邊界條件

根據文獻［10］中的實驗，設計如圖1所示的計算區域與初始流場。計算區域流向（x方向）長170mm，法向（y方向）高38mm；反應性預混氣體組成為C2H4＋3O2＋4N2，密度ρ0＝161.5g／m3，初溫T0＝293K；初始球形火焰半徑R0＝19mm，火焰中心（35mm，0），火焰區內密度ρ1＝15.78g／m3，火焰內外壓力均為p0＝13.3kPa；入射激波馬赫數1.7，初始時位于x＝12mm處，激波沿x方向從左向右傳播，激波后氣體狀態由Rankine－Hugoniot關系式給出。計算區域上邊界（y＝38mm）和x方向右端面為管壁，均采用無滑移的剛性絕熱壁面邊界；y＝0為對稱面，采用對稱邊界；x方向左端面處采用零梯度邊界。計算使用的均勻網格尺寸為47.5μm，由于預混氣體在本文條件下的火焰面厚度為約0.785mm［11］，因此火焰面厚度可由約16個網格刻畫，這個網格分辨率足以反映火焰界面的變化過程。此外，計算時間步長取8.55ns，使庫朗數小于0.2，滿足計算中時間推進的穩定性判據。由于本文中使用了較高的網格分辨率，計算量較大，因此采用自己發展的并行化設計的計算程序完成。

1.3 實驗驗證

數值計算算法和化學反應模型的可靠性，已在文獻［13］的計算中予以驗證。考慮到網格精度的進一步提高，依據文獻［10］的實驗結果對數值模型和化學反應參數做進一步驗證。圖2給出了各時刻激波陣面距點火位置的距離，以及激波誘導的變形火焰的寬度和高度，其中，計算和測量結果均采用火焰初始半徑R0進行量綱一化處理。從圖2可以看出，激波陣面距點火位置的距離與實驗結果很好吻合，而火焰尺寸的變化規律也與實驗結果一致，說明本文計算方法和化學反應各參數是合理和可靠的。

圖2 數值計算結果與實驗結果的對比Fig.2 Comparisons between calculated and experimental results

2 結果與討論

為深入認識激波與火焰的相互作用關系，主要從火焰演變特性（可視化結果）、火焰二維效應（積分量）、火焰分形維效應（界面形態）以及混合與燃燒的關系等方面予以討論和分析。

2.1 火焰演變特性

圖3～4分別給出了入射激波和反射激波與火焰作用的流場圖像，其中每幅子圖的上半部分對應密度分布，下半部分對應渦量分布。由圖3可見，當入射激波與火焰開始作用時，由于火焰表面的壓力梯度和密度梯度方向不一致，產生斜壓效應，進而在火焰表面形成渦量，因此初始時火焰迎風面發生凹陷，從而表現出RM不穩定誘導的大尺度變形（見圖3（a）～3（b））；隨著時間，由于火焰界面內外存在速度差，因而在火焰表面逐漸形成了KH不穩定誘導的小尺度離散渦結構（見圖3（c））；接下來，在入射激波作用后的一段時間內，產生的大尺度渦量逐漸發展至火焰中心區，而火焰界面處主要以小尺度渦量為主；由于界面處形成的渦量能卷吸環境中的未燃氣體，促進燃燒，因此火焰的面積明顯增加（見圖3（d）～3（f））。

當入射激波行至右端壁面后發生反射，反射激波與已變形的火焰再次作用，這使得火焰變形加劇。由圖4可見，在反射激波與火焰作用初期，火焰表面變形加劇，彎曲皺褶增多，小尺度渦結構也明顯增加（見圖4（a）～4（b））；當反射激波完全掃過火焰后，反射激波的誘導作用使變形火焰向壁面翻轉（見圖4（c）），這與實驗結果［10］一致；反射激波波后滯止的高溫高壓環境為火焰進一步燃燒膨脹提供了基礎，隨著時間，火焰面積迅速增加，變形火焰逐漸靠近上下壁面并沿流向方向膨脹（見圖4（d）～4（f））。

圖3～4還顯示了激波的運動過程。由于火焰內密度較小，所以入射激波在火焰內部傳播速度較快，能在火焰表面形成激波分歧，而反射激波在入射激波沿壁面誘導產生的邊界層內也發生了激波分歧。上述數值計算結果合理地描述了激波誘導火焰變形的過程，計算結果也與實驗很好符合，這為下面進一步的分析提供了可信的結果。

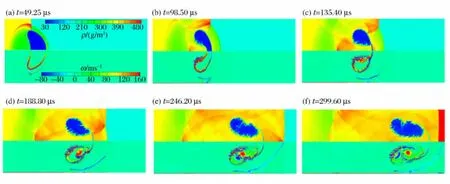
圖3 入射激波與火焰作用的密度和渦量場Fig.3 Densities and vorticities for the interaction between incident shock wave and flame

圖4 反射激波與火焰作用的密度和渦量場Fig.4 Densities and vorticities for the interaction between reflected shock wave and flame

2.2 火焰二維效應

采用積分量進行分析，可以從變形火焰整體發展行為考察其演變過程。采用積分形式定義火焰有效面積A和平均化學反應放熱率dh／dt，用來考察火焰變形的過程：

式中：D和F分別代表整個計算區域和火焰區（定義為反應物質量分數Y≤0.99），X代表反應物的體積分數，其中式（7）采用的火焰有效面積表征了整個計算域內去除混合影響之后的火焰面積。

圖5給出了量綱一火焰有效面積A／A0（A0為初始火焰面積）和平均化學反應放熱率dh／dt隨時間的變化過程。可見，火焰有效面積的變化經歷了4個階段：階段Ⅰ為入射激波壓縮階段（0～94μs），與此對應的火焰有效面積在壓縮作用下逐漸變小；階段Ⅱ為火焰膨脹階段（94～328μs），此時激波已掠過火焰，燃燒放熱使火焰開始膨脹，面積逐漸增加；階段Ⅲ為反射激波壓縮階段（328～374μs），此時變形火焰在反射激波的壓縮下面積再次變小；階段Ⅳ為火焰再次膨脹階段，由于反射激波波后介質處于高溫高密度的滯止狀態，這為化學反應速率的提高提供了有利條件，所以火焰燃燒膨脹加劇、面積迅速增加。圖5中平均燃燒反應放熱速率的變化顯示，壓縮階段（階段Ⅰ和Ⅲ）放熱速率呈現持續增長的趨勢，說明激波壓縮作用提供的高溫高密度環境可以促進化學反應的進行，尤其反射激波與變形火焰的再次作用可以顯著提高火焰的放熱速率；入射激波作用后的火焰膨脹階段（階段Ⅱ），放熱速率則基本維持在一個恒定值，而反射激波作用后的火焰膨脹階段（階段Ⅳ），放熱速率持續上升到一定值后維持一段時間隨后又開始下降，盡管如此，反射激波作用后（階段Ⅳ）的放熱速率比入射激波作用后（階段Ⅱ）的放熱速率增加約一個數量級，這反映了反射激波對燃燒過程的巨大促進作用。

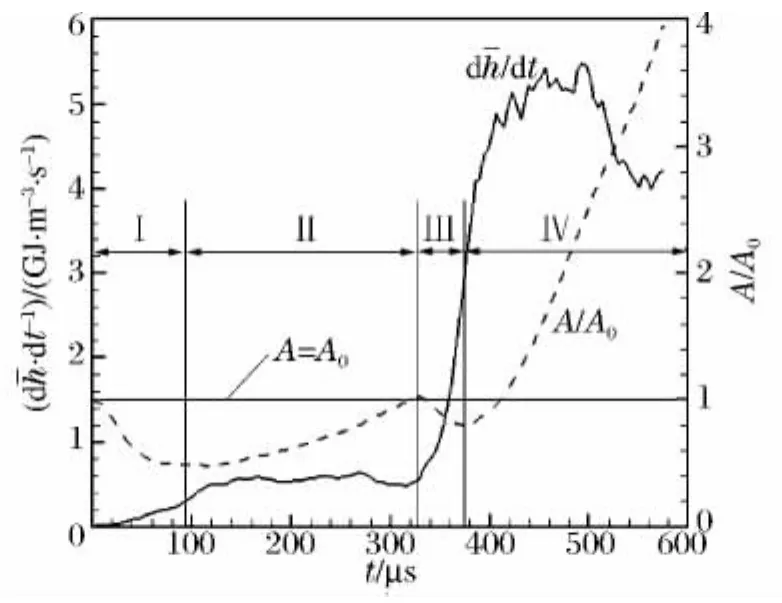
圖5 火焰的有效面積和平均反應放熱率Fig.5 Effective area and average reaction heat release rate

2.3 火焰分形維效應

圖3～4表明，火焰界面在激波的作用下呈現皺褶和小尺度渦的形態。由于預混火焰的燃燒過程主要發生在未燃氣與已燃氣的界面處，為了反映火焰界面的形態和幾何自相似行為對燃燒過程的影響，對數值模擬得到的二維計算結果進行圖像處理，獲得了火焰界面量綱一長度L／R0和火焰界面平均分形維數Dm隨時間變化的結果，如圖6所示。其中，分形維數Dm的處理采用了基于質量分數Y＝0.99的火焰界面的數盒子處理方法，根據不同盒子尺寸ε，可以獲得覆蓋火焰界面的不同盒子個數N（ε），由此可計算二維火焰界面分形維數：該量的變化反映了火焰表面小尺度渦誘導的界面皺褶程度。圖6中，誤差棒代表不同盒子取樣位置所確定的分形維數的最小和最大值，陰影區所處的分形維范圍表征充分發展湍流中的幾何自相似性。

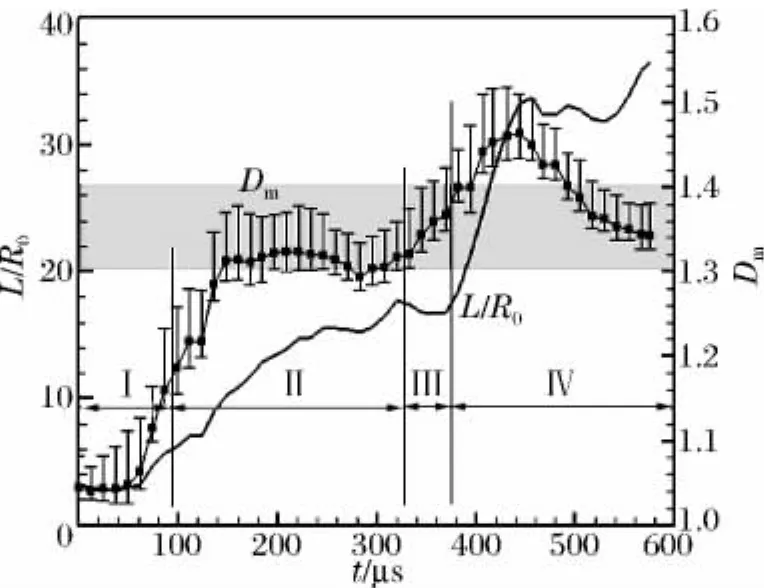
圖6 火焰界面長度和分形維數Fig.6 Interface length and fractal dimension

由圖6可以發現，火焰界面長度變化并不完全遵循圖5中的火焰有效面積4個階段變化規律。反射激波作用前（階段Ⅰ和Ⅱ），界面長度持續增長，而界面分形維數在階段Ⅰ和階段Ⅱ前期（t＜150μs）也快速增長（Dm由1.04增至1.32），這表明，入射激波作用引起的火焰小尺度皺褶占據主導；到階段Ⅱ后期（150～327.9μs），火焰界面分形維數維持在1.29～1.33之間，表明火焰皺褶程度不再明顯增加，而此時火焰界面長度仍在持續增加，由于此階段火焰膨脹并不明顯且反應放熱速率維持在較小值（見圖5），這意味著入射激波誘導的大尺度火焰變形拉伸使火焰界面長度繼續增加。因此，在反射激波與火焰作用之前，物理過程對火焰的變形和皺褶起主導作用。當反射激波與變形火焰再次作用時（t＝328μs），火焰界面長度經短暫的減小（階段Ⅲ）后，又持續增長至階段Ⅳ前期（t＝450μs），而這一過程中，界面分形維數又經歷一個持續上升的過程（Dm由1.33增至1.46）。由于此階段化學反應放熱速率急劇增加至最大值（見圖5），可以斷定，激波誘導的火焰表面皺褶程度的增加和燃燒導致的火焰膨脹，共同促進了界面長度的增長。然而，從階段Ⅳ后期開始（t＞450μs），火焰界面長度不再增加，界面分形維數開始下降，這說明由于界面皺褶程度的減少導致界面長度有減小的趨勢，但是此階段火焰仍在膨脹，又促使了界面的增長，因此綜合的效果是火焰界面長度維持在一定的范圍。階段Ⅳ后期的變化表明，燃燒過程對火焰的皺褶有一定的抑制作用，這主要體現在后期火焰界面皺褶程度的降低，由于皺褶的減少會減小火焰界面未燃氣和已燃氣接觸的長度，因此反過來又會抑制反應放熱過程，這個特點在反應放熱速率階段Ⅳ后期的下降（見圖5）中可以得到體現。

為比較火焰在不同膨脹階段（階段Ⅱ和Ⅳ）的發展規律，表1給出了火焰有效面積A、火焰特征長度l和火焰界面長度L等幾何量在各階段的平均增長率，其中，特征長度定義為計算區域內半圓形火焰理想狀態下（即不受變形影響）的周長。表中，ηA＝ΔA／Δt，ηl＝Δl／Δt，ηL＝ΔL／Δt，ηⅣ／ηⅡ代表了階段Ⅳ和Ⅱ火焰各幾何量平均增長率的比，用于考察反射激波作用前后的影響，而ηL／ηl則表征了火焰界面在激波作用后的變形和皺褶程度。由此可以看出，反射激波作用后的火焰各幾何量增長均比作用前的幾何量增長有成倍增加，而在階段Ⅱ和Ⅳ，ηL／ηl分別達到11.57和13.21，這說明激波導致火焰變形和皺褶現象十分顯著，尤其在階段Ⅳ前期，這與圖3～4反映的規律相同。

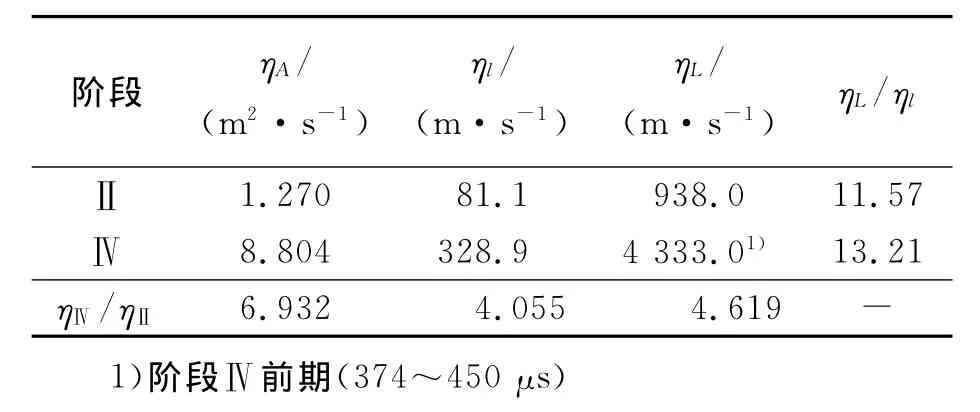
表1 階段Ⅱ和Ⅳ火焰幾何量平均增長速率的變化Table 1 Variation of the average increase rate of geometrical parameters in stagesⅡandⅣ

圖6中的陰影區域代表了文獻［14－15］給出的RM不穩定誘導的惰性界面湍流混合的分形維數范圍（Dm＝1.3～1.4），在此范圍內，變形界面表現出具有充分發展湍流特性的幾何自相似特征。計算結果表明，激波誘導的火焰變形在階段Ⅱ膨脹后期（t＞150μs）已經進入該范圍，并且在反射激波作用后甚至超過該范圍，盡管后期Dm有所下降，但仍未低于該范圍，這說明激波誘導的火焰于入射激波作用后不久便呈現了湍流燃燒的形式。

2.4 混合與燃燒的關系

預混火焰不同尺度的變形增加了火焰界面兩側未燃氣和已燃氣的接觸表面，可以強化兩者之間的混合過程，這對于促進燃燒過程是有利的。但是上述結果也表明，在反射激波作用的后期，燃燒過程會弱化火焰表面的皺褶程度，因而在一定程度下抑制了混合過程。在有關界面混合的討論中，J.Yang等［16］首先引入拉伸率概念定量表征混合過程，并考察了激波強度、密度比、界面幾何構型等對混合的影響；S.Kumar等［17］沿用前者的思路，對激波與5種不同構型的SF6氣柱界面的作用進行了實驗研究，發現初期（t≤220μs）質量線的拉伸率呈指數變化，但這種方法不能描述后期的混合情況；J.H.J.Niederhaus等［18］針對激波與不同密度氣泡界面作用的三維數值模擬結果，定義了氣泡區域內環境氣體所占的體積分數為混合度，用于描述混合。但是上述研究僅僅考慮了混合作用，而在激波與火焰界面作用的過程中，燃燒放熱會與混合相互影響，但目前尚還未見到對混合與燃燒相互關系的具體描述。因此，為深入分析這兩者的關系，本文中定義一個量綱一數η，用以表征火焰區域內總質量變化率與燃料消耗速率的比，表達如下：

式中：分子項代表火焰區（Y≤0.99）未燃氣體混入速率，分母項代表火焰區未燃氣體燃燒消耗速率。因此，當η＞1時，表示混合速率大于燃燒速率，混合過程占主導地位，當η→1時，則表示進入火焰區的未燃氣速率接近燃燒速率，這代表了以火焰傳播為主導的燃燒模式。

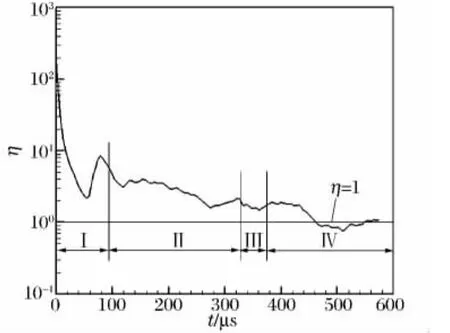
圖7 火焰區域內總質量變化率與燃燒消耗速率的比Fig.7 Ratio of the total mass change rate to the burning consumption rate within the flame

圖7顯示了η隨時間的變化過程，可以看出，η在階段Ⅰ初期混合的影響逐漸下降、燃燒的影響逐漸增強，但混合過程仍占主導；在階段Ⅰ后期，由于入射激波與火焰界面相互作用產生渦量，使得混合大大增強，所以η又開始上升；在隨后的各階段中，η緩慢震蕩降低，表明火焰變形同時受到混合與燃燒作用的影響，且燃燒作用慢慢增強；在階段Ⅳ后期，該值基本在1附近震蕩，說明反射激波后的火焰發展主要以火焰傳播的方式進行，混合作用已經很小。上述結果表明，未燃氣體與可燃氣體的混合會促進燃燒，但逐漸增強的燃燒作用能迅速地消耗混入火焰內的未燃氣，反過來抑制混合。

3 結 論

采用帶單步化學反應的NS方程和高網格分辨率，對平面入射激波及其反射激波誘導火焰變形過程進行數值研究，利用實驗結果驗證了計算模型和參數的可靠性。提出并采用流場可視化、火焰積分量、火焰界面幾何特性等分析手段探討了火焰變形、燃燒放熱和混合等過程的變化規律及其相互作用關系。結果表明，初始球形火焰在激波及其反射波的各次作用下均表現出先壓縮再膨脹的特點，反射激波作用前，激波的誘導作用對火焰變形和表面皺褶起到了主要作用，此階段以物理過程為主導；反射激波作用后，變形火焰放熱速率增加約1個數量級，表征火焰形態的各幾何量均成倍增加，主導火焰發展的上述物理過程逐漸由化學反應過程所替代，尤其是在火焰發展后期，化學反應的增強會反過來抑制火焰界面的皺褶，進而弱化了界面兩側已燃氣和未燃氣之間的混合，使火焰發展主要受燃燒過程控制而非混合過程控制。

［1］Maran S P，Sonneborn G，Pun C S J，et al.Physical conditions in circumstellar gas surrounding SN 1987A12years after outburst［J］.Astrophysical Journal，2000，545（1）：390－398.

［2］Marble F E，Hendrick G J，Zukoski E E.Progress toward shock enhancement of supersonic combustion process［R］.AIAA 87－1880，1987.

［3］Oran E S，Gamezo V N.Origins of the deflagration－to－detonation transition in gas－phrase combustion［J］.Combustion and Flame，2007，148（1／2）：4－47.

［4］Markstein G H.A shock－tube study of flame front－pressure wave interaction［C］∥6th Symposium （International）on Combustion.Pittsburgh，USA：The Combustion Institute，1957：387－398.

［5］Ton V T，Karagozian A R，Marble F F，et al.Numerical simulations of high speed chemically reactive flow［J］.Theoretical and Computational Fluid Dynamics，1994，6（2／3）：161－179.

［6］Ju Y，Shimano A，Inoue O.Vorticity generation and flame distortion induced by shock flame interaction［C］∥27th Symposium （International）on Combustion.Pittsburgh，USA：The Combustion Institute，1998：735－741.

［7］Khokhlov A M，Oran E S，Chtchelkanova A Y，et al.Interaction of a shock with a sinusoidally perturbed flame［J］.Combustion and Flame，1999，117（1／2）：99－116.

［8］Khokhlov A M，Oran E S，Thomas G O.Numerical simulation of deflagration－to－detonation transition：The role of shock－flame interactions in turbulent flame［J］.Combustion and Flame，1999，117（1／2）：323－339.

［9］Khokhlov A M，Oran E S.Numerical simulation of detonation initiation in a flame brush：The role of hot spots［J］.Combustion and Flame，1999，119（4）：400－416.

［10］Thomas G O，Bambrey R，Brown C.Experimental observations of flame acceleration and transition to detonation following shock－flame interaction［J］.Combustion Theory and Modelling，2001，5（4）：573－594.

［11］Dong G，Fan B C，Ye J F.Numerical investigation of ethylene flame bubble instability induced by shock waves［J］.Shock Waves，2008，17（6）：409－419.

［12］Chakravarthy S R，Osher S.A new class of high accuracy TVD schemes for hyperbolic conservation laws［R］.AIAA 85－0363，1985.

［13］朱躍進，董剛，范寶春.受限空間內激波與火焰作用的三維計算［J］.推進技術，2012，33（3）：405－411.Zhu Yue－jin，Dong Gang，Fan Bao－chun.Three－dimensional computation of the interactions between shock waves and flame in a confined space［J］.Journal of Propulsion Technology，2012，33（3）：405－411.

［14］Vorobieff P，Rightley P M，Benjamin R F.Shock driven gas curtain：Fractal dimension evolution in transition to turbulence［J］.Physica D：Nonlinear Phenomena，1999，133（1）：469－476.

［15］Ng H D，Abderrahmane H A，Bates K R，et al.The growth of fractal dimension of an interface evolution from the interaction of a shock wave with a rectangular block of SF6［J］.Communications in Nonlinear Science and Nu－merical Simulation，2011，16（11）：4158－4162.

［16］Yang J，Kubota T，Zukoski E E.Applications of shock－induced mixing to supersonic combustion［J］.AIAA Journal，1993，31（5）：854－862.

［17］Kumar S，Orlicz G，Tomkins C，et al.Stretching of material lines in shock－accelerated gaseous flows［J］.Physics of Fluids，2005，17（8）：082107.

［18］Niederhaus J H J，Greenough J A，Oakley J G，et al.A computational parameter study for the three－dimensional shock－bubble interaction［J］.Journal of Fluid Mechanics，2008，594：85－124.