基于線段操作的多邊形求交算法研究

鮑其勝，王 慶，何立恒

(1.南京市測繪勘察研究院有限公司，江蘇南京210005;2.南京林業(yè)大學土木工程學院，江蘇南京210037)

兩個多邊形求交是計算幾何的基本問題之一，應用十分廣泛。地圖制圖中的圖面要素壓蓋處理、地理信息系統(tǒng)中不同類別多邊形拓撲疊加分析、計算機輔助設計中的文字、圖塊消隱等都直接或間接地用到多邊形求交［1-3］。在進行土方計算時，需要將計算邊界之外的格網(wǎng)刪剪掉，實際也是多邊形求交。邊界外框是由邊界點坐標系列中(Xmin，Ymin)為左下角、(Xmax，Ymax)為右上角的矩形，計算邊界包含于邊界外框內。對邊界范圍內的區(qū)域計算，以計算邊界外框循環(huán)得到的格網(wǎng)跟計算邊界有相交、包含和分離3種關系。為了摒棄計算邊界范圍外的網(wǎng)形，需要進行所構網(wǎng)形與邊界的相互關系判別并求交，得到邊界內的網(wǎng)形。

一、幾個關系判別算法

1.多邊形相互關系判別

本文所討論的多邊形是在同一水平面或投影到同一水平面上的簡單多邊形，多邊形相互關系判別如圖1所示。將多邊形看做是封閉的線實體，通過求線實體的交點個數(shù)來判斷兩個多邊形的相互關系。若沒有交點，則為包含或分離(非包含);若有交點，則為交叉關系。包含和分離關系的判定實質是點與多邊形的關系判定，若頂點都在計算邊界范圍內，則是包含關系;若頂點都不在計算邊界內，則是分離關系。

圖1 多邊形相互關系示意圖

2.點和多邊形相互關系判別

在點與多邊形相互關系判定中，采用射線交點法進行判定［4-5］。以待判定點為起點作任意射線，通過射線與多邊形邊界交點的奇偶性來確定，若交點數(shù)為奇數(shù)，則點在多邊形內;若交點數(shù)為偶數(shù)，則在多邊形外。通常射線由一段超出多邊形范圍的水平線段代替，此線段的一端點為待判定點，另一端點則是水平向右或向左的多邊形范圍外任一點，如圖2所示。但圖3是交點為多邊形頂點的情況，此法則失效。因此，在判定之前，要明確點是否在多邊形的邊界上。圖3中，圖3(a)有1個交點，圖3(b)有3個交點，圖3(c)有4個交點，圖3(d)有2個交點，僅以交點的奇偶數(shù)進行判別，圖3(b)、圖3(d)與事實不符。因此，在實際計算交點個數(shù)時，要特別判定交點是否為多邊形的一個頂點或在多邊形線段上。因此，設定一原則，多邊形以交點為線段一端點的兩連續(xù)線段位于射線左右來制定，位于兩側的為1個交點，位于同側或線上的為0個交點或2個交點。

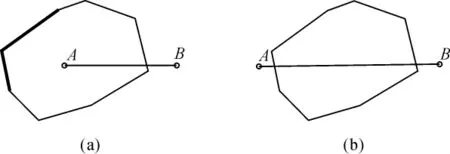
圖2 點和多邊形相互關系示意圖

圖3 點在多邊形內外判定交點幾種特殊情況

二、求交叉關系算法與實現(xiàn)

1.算法思路

國內外研究人員對多邊形求交作了深入研究。楊維芳［6］給出兩數(shù)組記錄交點后，對數(shù)組遍歷求交;朱愛軍等［7］在交點序列基礎上擴充成節(jié)點序列，通過遍歷序列求交;杜爽等［8］在交點結構中記錄與交點相關的節(jié)點信息，如出入狀態(tài)、交點位置等來求解;宋立明等［9］采用雙向鏈表數(shù)據(jù)結構，對兩簡單多邊形的頂點及交點進行插入存儲，通過遍歷兩個頂點、交點混合表來達到求交目的。上述研究的核心都是求出多邊形交點，然后進一步對點操作，本文則另辟蹊徑，在求出多邊形交點后，對由多邊形節(jié)點和交點組成的子線段進行操作，判斷所構成的子線段是否屬于公共線段，以構成公共線段集，遍歷公共線段，連接成閉合多邊形求交。

2.算法過程

圖4有兩個多邊形M、N，求交叉公共多邊形需分步進行。

1)選擇多邊形并判定兩多邊形的相互關系。將平面M作為目標多邊形，平面N作為源多邊形。利用交點個數(shù)判斷兩多邊形的相互關系，若相交，繼續(xù)下一步;若分離，結束計算;若包含，留下被包含圖形后結束計算。

2)求交點。選取目標多邊形M中線段M1M2與源多邊形N的每條線段求交點，若線段M1M2與源多邊形N邊界有交點，將所有交點去掉重復點后，連同從目標多邊形所選定線段M1M2的端點按此線段的一定方向排序，如圖4所示，M1、P1、…、Pn、M2為排序的系列點。其中，M1、M2為目標多邊形的線段端點;P1、…、Pn為線段M1M2與源多邊形N的所有交點。

圖4 求公共面

兩線段p1p2和q1q2交點一般為圖5幾種情形，本算法中的交點個數(shù)分別為：圖5(a)為J一點，圖5(b)為p2一點，圖5(c)為p2(或q1)一點，圖5(d)為p2和q1兩點，圖5(e)為p1和p2兩點，圖5(f)為q1(或p1)和q2(或p2)兩點。

圖5 線段交點關系圖

3)找公共線段。將端點和交點依順序兩兩作子線段，即 M1P1、P1P2、…、PnM2為依次連接的線段，求各線段的中點，根據(jù)點在多邊形內外判定方法判斷中點與源多邊形N的相互關系，若線段的中點在源多邊形內或在源多邊形邊界上，則此線段也在源多邊形內或在源多邊形邊界上，此線段即為公共線段，將此線段及線段的兩個端點坐標記錄在數(shù)據(jù)選擇集中，直至所有兩兩點連成的線段判定完畢。圖4中線段P1P2和P3P4即為公共線段。

4)選取構成目標多邊形M的下一個線段，重復步驟2)和步驟3)，直至構成目標多邊形M的所有線段與源多邊形N求交點計算完畢，然后判斷各相鄰點連成的線段是否在源多邊形內或邊界上，若在源多邊形內或邊界上，即為公共線段并記錄至公共數(shù)據(jù)選擇集中。

5)將目標多邊形和源多邊形對調，原源多邊形作為目標多邊形，原目標多邊形作為源多邊形，重復步驟2)～步驟4)。進行步驟3)操作時，若線段的中點在源多邊形內，記錄至公共線段;若線段的中點在源多邊形邊界上，因目標多邊形和源多邊形對調前已記錄，對調后將不再記錄，避免重復。

6)遍歷公共線段，構建兩多邊形交集。從公共線段數(shù)據(jù)選擇集中取出任一線段，根據(jù)此線段端點坐標，在公共線段數(shù)據(jù)選擇集中找與其首尾相連的線段，將它們連接起來，依次找出與連接圖形端點相同的其他線段并連接，組成封閉多邊形。在尋找過程中，選中的線段就從公共線段數(shù)據(jù)選擇集中刪掉。

7)若組成一個封閉多邊形后，公共線段數(shù)據(jù)集中還有線段，重復步驟6)，直至公共線段數(shù)據(jù)集中沒有線段，此時構成的所有封閉多邊形即為所求的兩多邊形交集。

三、算法分析比較

1)本算法是在求交點后，組成子線段進行判斷并求交，判斷過程中已考慮重邊或重點等問題。楊維芳［6］使用數(shù)組只能表示一個交點，對重邊有兩個交點的不能表示;朱愛軍、杜爽等［7-8］采用交點序列或出入狀態(tài)判別，過程復雜，尤其對重邊、重點要單獨考慮，顯得繁瑣;宋立明等［9］采用了雙向鏈表數(shù)據(jù)結構，沒有解決重邊或重點問題。

2)上述已有算法的記錄方式都有兩組數(shù)組、序列或鏈表，探測對象是節(jié)點，探測方向都是在兩組存儲數(shù)據(jù)中轉換。本算法采用由節(jié)點和交點組成的子線段為探測對象，形成一組公共線段集，遍歷公共線段數(shù)據(jù)集求交，探測對象及探測方法包羅了重邊或重點的情況。

3)從算法的時間上比較，求交點與已有算法基本一致;在探測每一線段及交點時，已有算法只對交點操作，本算法探測節(jié)點和交點組成的子線段，每條邊多一次探測，總共多出兩多邊形邊數(shù)總和;在遍歷時間上，本算法只對公共線段數(shù)據(jù)集遍歷，明顯比已有算法要短;總體時間與已有算法相當。

4)在存儲單元上，本算法存儲的是公共線段，已有算法存儲的是節(jié)點和交點，本算法遠優(yōu)于已有算法。

5)本算法在進行子線段探測時，只需改變探測條件，即可實現(xiàn)兩多邊形的求差和求并。

四、結束語

本算法過程簡單、思路嚴謹，考慮到地圖的復雜性和特殊性，運算結果精度和圖形輸出質量高。若算法基于AutoCAD平臺來實現(xiàn)，利用二次開發(fā)工具VBA中object.IntersectWith函數(shù)的返回值求交點個數(shù)及交點坐標，使得計算過程更簡單，運行效率更高。連線利用AutoCAD中的數(shù)據(jù)選擇集，在數(shù)據(jù)存儲空間上和搜尋時間上效率又一步得到提高。

求公共面算法主要是針對計算機地圖制圖、地理信息系統(tǒng)、計算機輔助設計等領域中多邊形求交，即著重于地圖上多邊形的交集運算。本算法易于編程實現(xiàn)，計算工作量小，求交效率高，已成功應用在土方計算軟件開發(fā)中，在計算機圖形和地理空間信息等方面可以廣泛應用。

［1］謝忠，魏東琦，吳亮，等.簡單矢量數(shù)據(jù)多邊形裁剪問題的圖模型［J］.測繪學報，2009，38(4)：369-374.

［2］劉勇奎，高云，黃有群.一個有效的多邊形裁剪算法［J］.軟件學報，2003，14(4)：845-856.

［3］彭杰，劉南，唐遠彬，等.一種基于交點排序的高效多邊形裁剪算法［J］.浙江大學學報：理學版，2012，39(1)：107-111，122.

［4］董秀山，劉潤濤.判斷點與簡單多邊形位置關系的新算法［J］.計算機工程與應用，2009，45(2)：185-186.

［5］陳瑞卿，周健，虞烈.一種判斷點與多邊形關系的快速算法［J］.西安交通大學學報，2007，14(1)：59-63.

［6］楊維芳.兩個復雜多邊形求交的矢量算法［J］.蘭州鐵道學院學報：自然科學版，2002，21(1)：108-110.

［7］朱愛軍，鄧安福，魏艷軍，等.以節(jié)點操作確定兩任意實心多邊形交集的方法［J］.重慶大學學報：自然科學版，2004，34(12)：56-59.

［8］杜爽，陳成永.以節(jié)點操作實現(xiàn)多邊形求交的算法［J］.測繪通報，2007(10)：21-24.

［9］宋立明，閆浩文，王邦松，等.兩個簡單多邊形求交的算法［J］.測繪與空間地理信息，2011，34(1)：258-260.

［10］張帆.AutoCAD VBA二次開發(fā)教程［M］.北京：清華大學出版社，2006.