商用車駕駛室橫拉桿故障問題的試驗研究及改進設計
李德光,韋志林
(1.東風柳州汽車有限公司技術中心,廣西 柳州545005;2.廣西工學院汽車工程研究所,廣西 柳州545006)
目前的商用車普遍采用全浮式駕駛室以提高舒適性。為了減小駕駛室的側傾運動幅度,在全浮式駕駛室后部設計安裝了橫向的拉桿裝置(如圖1所示),以提高駕駛室的側傾剛度[1]。然而某型商用車在海南試驗場進行可靠性試驗時駕駛室橫向拉桿發生了彎曲失穩變形、接頭襯套斷裂等故障現象。

圖1 駕駛室橫拉桿布置示意圖
根據橫拉桿的具體工作特點,該桿件在車輛在不平路面行駛時會承受來自兩種駕駛室運動引起的載荷:其一是當駕駛室存在側向加速度時橫拉桿主要承受軸向的拉力或壓力;其二當駕駛室繞X軸做擺動時會主要承受彎矩和扭矩。車輛在實際的行駛時往往是多種載荷同時出現,且這種在動態才會出現的載荷無法用靜態計算進行分析,鑒于關于這方面的數據和相關的資料的空缺,進行相關的動態內力的電測試驗并在試驗基礎上進行結構的再設計是有必要的。
1 橫拉桿內力測試
通過電測試驗測定橫拉桿在可靠性路面上所受的應力和的內力(軸力、彎矩、扭矩),可以對橫拉桿的強度做出評估,并對結構故障的原因進行分析,提出具體的改進意見。
1.1 內力測試原理
這里以一個受軸力和彎矩作用的箱形截面的梁的內力測量為例,說明用電測法測量內力的原理[2]。

圖2 軸力的內力測試
如圖2所示,為了測量梁的受力,在梁的同一截面的3個位置布置了沿X軸方向的應變片。顯然,應變片的測量值是梁所受軸力和彎矩共同作用的結果。這里規定若彎矩的矢量方向與相應的坐標軸方向相同則彎矩為正,與坐標軸方向相反則為負。因此,有如下等式成立:
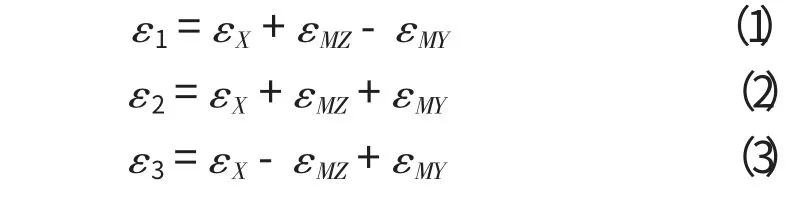
其中,
ε1、ε2、ε3為位置1、2、3處應變的測量值;
εX為由軸力引起的應變;
εMZ為由繞Z軸的彎矩引起的應變;
εMY為由繞Y軸的彎矩引起的應變;
ε1、ε2、ε3的值可以由測量儀器中讀出,然后求解(1)、(2)、(3)式組成的方程組有:

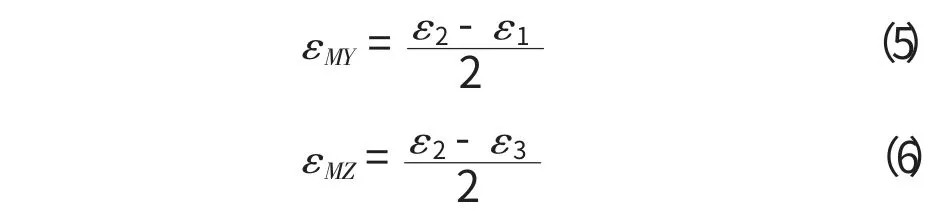
由材料力學知,軸力和彎矩引起的應變可以按式(7)、(8)計算:
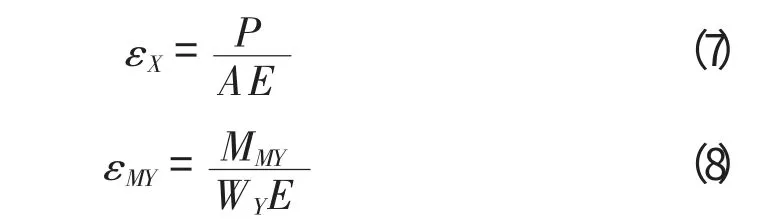
其中,
P為桿件所受的軸力;
A為桿件的橫截面積;
E為桿件材料的彈性模量;
MY為矢量方向平行于Y軸的彎矩;
WY為繞Y軸的抗彎截面模量。
將它們分別代入(4)、(5)、(6)得到:
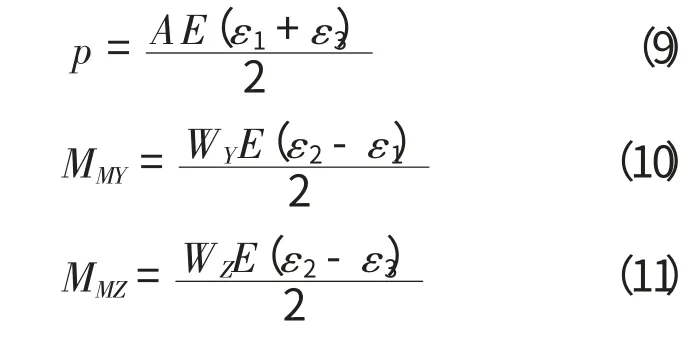
上述推導說明了軸力和彎矩的測量原理,對于扭矩等其它形式的內力也可以采用類似的方法加以測量。
1.2 測試對象慣性參數的計算
原桿件采用的是2 mm厚度的空心軸,其尺寸如下:
內徑d=18 mm,外徑D=22 mm,截面積:
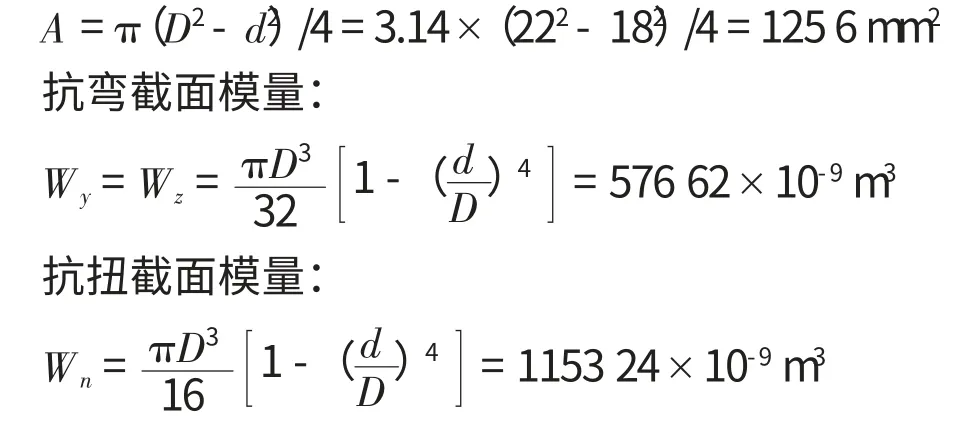
1.3 測點布置
為測定橫拉桿所受的應力和內力,需要在橫拉桿的中部和兩端布置測點。由前述的內力計算公式可知,軸力的計算結果對測量的應變值的變化比較敏感,測量誤差對軸力有放大作用,測量誤差產生的原因有橫拉桿尺寸公差、應變片電阻誤差、應變片貼片位置方位誤差、測量時溫度變化影響、儀器不穩定產生誤差等因素。因此在未知彎矩、軸力、扭矩大小的情況下,本次實驗在多個截面上布置測點,這樣可以對計算出來的內力進行比較核對。
在布置測點時,按軸力、彎矩、扭矩的測試方法進行,測點布置方案如圖3所示。各組測點的用途如下:
(1)測定1、2、3、4用于測定接頭附近的應力。由于接頭附近曾經出現斷裂的現象,因此應變片的方位需與以前出現裂紋的方向垂直。
(2)測點6與8、14與16、18與20組成3組,用于測量3個截面處橫拉桿所受的垂直彎矩。
(3)測點5與7、13與15、17與19組成3組,用于測量3個截面處橫拉桿所受的水平彎矩。
(4)測點18與21、20與22組成兩組測量橫拉桿所受的軸力。
(5)測點9、10、11、12用于測量橫拉桿的扭矩。
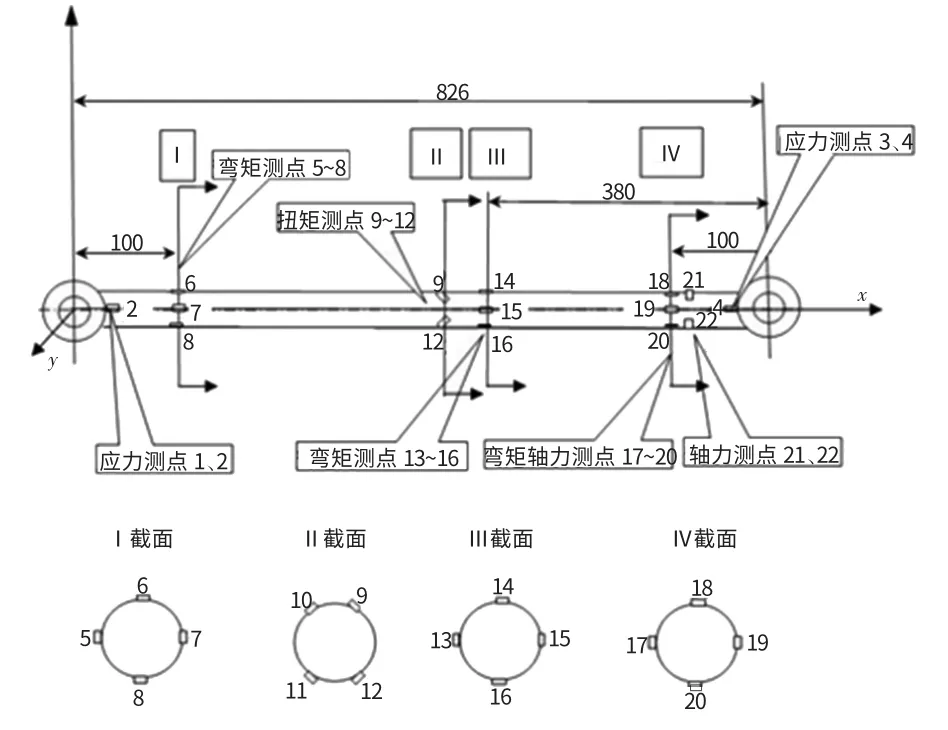
圖3 測點布置示意圖
1.4 測試數據
在海南汽車試驗場可靠性跑道上進行實車測試,如圖4為截面測點2的應變動態曲線。根據前述介紹的內力計算公式,計算出橫拉桿在可靠性路面上所承受的載荷,如表1所示。
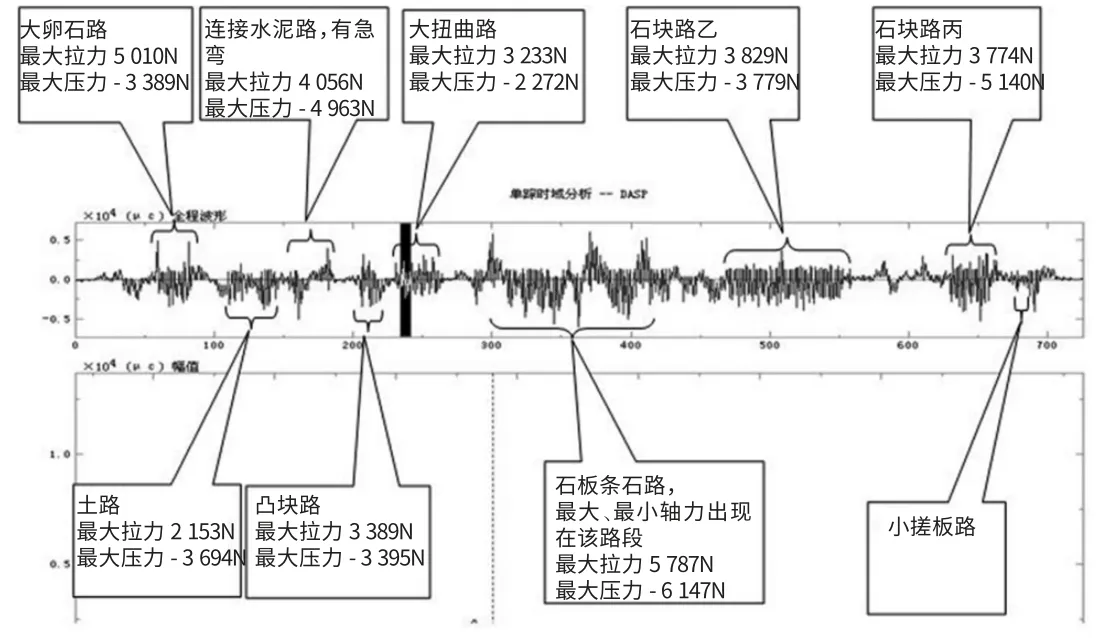
圖4 測點2動態曲線及典型路段最大軸力數值

表1 各截面彎矩幅值統計
實驗數據表明橫拉桿主要承受的是軸力,彎矩和扭矩很小。
在同一截面選取不同的測點對計算軸力和彎矩所得結果略有不同,由于內力必須在測定應力的基礎上經過相關的計算才可獲得,而應變片的電阻值誤差、貼片角度誤差、構件尺寸誤差,導線電阻值的誤差都會對最終的結果造成影響。因此本次試驗才在多個截面上電測試驗,以獲得較大軸力數據。
2 橫拉桿失穩的屈曲有限元計算
屈曲分析主要用于研究結構在特定載荷下的穩定性以及確定結構失穩的臨界載荷。線性屈曲分析是以小位移小應變的線彈性理論為基礎的,分析中不考慮結構在受載變形過程中結構構形的變化,也就是在外力施加的各個階段,總是在結構初始構形上建立平衡方程。當載荷達到某一臨界值時,結構構形將突然跳到另一個隨遇的平衡狀態,稱之為屈曲。臨界點之前稱為前屈曲,臨界點之后稱為后屈曲[3]。
利用hyperWorks結構設計分析軟件包,建立橫拉桿的有限元模型。模型中包含23 733個hex8實體單元,節點數為14 787。在橫拉桿的一端施加鉸鏈約束,在拉桿的另一端施加大小為10 N的軸向力,利用Optistruct求解器計算橫拉桿的10階失穩模態,結果如表2所示,失穩臨界載荷為特征值與載荷的乘積。

表2 失穩計算結果
3 結構改進設計
對拉桿失穩的計算表明,對應2毫米厚度桿的失穩臨界壓力為5 166 N,試驗所獲得的2毫米拉桿最大軸壓力為6 147 N,所以在車輛可靠性試驗時拉桿發生了明顯的失穩,失穩又直接導致應力的提高造成桿件高應力區的斷裂。
由于空間布置的限制,現有的橫拉桿外輪廓尺寸不能有明顯的變化。為了提高該桿件的失穩臨界載荷,將該橫拉桿改為外徑為φ22 mm、內徑為φ14 mm,即厚度為4 mm的空心圓管。
經計算,改進后的橫拉桿一階失穩臨界載荷提高為9 720 N,較原設計方案增加了88%。由于駕駛室的連接結構并沒有變化,因此工作時橫拉桿的最大軸向壓力不變,改變橫拉桿厚度后,該結構的失穩安全系數為9 720/6 147=1.58。
為了驗證新尺寸橫拉桿的可靠性,在海南試驗場重新進行了可靠性試驗,沒有出現前述的各種故障。該車投入市場后也沒有發生橫拉桿斷裂的情況,證明改進是有效的。
4 結束語
故障問題的成功解決表明我們關于橫拉桿失穩的分析與實際情況符合,不僅解釋了拉桿結構失效的機理,同時測定出實際的內力大小、幅值的統計等。這些數據對認識駕駛室實際工作狀態是必不可少的資料,填補了公司駕駛室設計相關數據的空白,對今后的設計工作有實際的參考和借鑒的意義。
[1]葉福恒,許 可,等.某商用車駕駛室全浮式懸置系統開發[J].汽車技術,2010(06):33-39.
[2]吳宗岱,袁禮平.應變電測原理及技術[M].北京:國防工業出版社,1982.
[3]李楚琳,張勝蘭,等.Hyperworks分析應用實例[M].北京:機械工業出版社,2008.

