一維彈道修正彈氣動分析與射程修正控制算法*

魏志芳，郎 田，吳建萍

(1中北大學機電工程學院，太原 030051;2駐763廠軍事代表室，太原 030008)

0 引言

一維彈道修正彈的主要工作原理是在炮彈發射時，瞄準比實際目標稍遠的一點發射，在炮彈飛行過程中，通過彈道偏差探測裝置測量出實際彈道，并與理想彈道進行比較，得出偏差，發出控制指令，在適當的時刻展開炮彈頭部引信上的阻力器，以增大炮彈頭部的徑向面積，從而增大炮彈所受空氣阻力，減小射程，接近目標，以達到修正的目的[1－3]。簡單一點說，一維彈道修正彈就是采用“打遠修近”的方式進行射程修正。

文中討論的是火箭增程一維彈道修正炮彈，彈丸發射后火箭助推裝置先工作，以增加射程。當助推結束，通過實時測量彈丸彈道參數，作為彈道初值，計算彈道預計落點，與目標進行比較，解算修正量，控制阻力環打開時刻，增大作用在炮彈上的空氣阻力，調整炮彈落點處縱向的位置，實現一維彈道修正的目的。影響一維彈道修正射程精度最關鍵的因素是阻力環結構、阻力環打開時刻的準確性與彈道探測的準確度。

1 一維彈道修正彈氣動特性分析

采用阻力環裝置的一維彈道修正彈是在普通旋轉彈的頭部增加阻力環裝置，因此氣動力計算包括阻力環未展開前的旋轉彈氣動力計算和阻力環展開后的氣動力計算。由于傳統工程氣動力算法不能考慮阻力環結構對彈丸氣動特性的影響，風洞試驗成本昂貴，文中采用數值模擬方法分析不同阻力環結構模型方案的增阻情況，為一維彈道修正彈阻力環結構設計提供參考。

首先采用數值模擬方法，對文獻中已有的算例進行氣動力特性計算，將計算結果與文獻的實驗結果進行比較分析，驗證了數值模擬計算模型的可行性。在此基礎上，分析了不同阻力環結構的一維彈道修正彈的氣動特性，比較其增阻情況。

1.1 算例驗證

選取文獻[4]中已有試驗數據的模型(彈徑為38mm，全長為198.47mm)，如圖1所示，使用 CFD軟件對該彈進行零攻角的繞流流場的數值模擬，得到其阻力系數，與文獻[4]中的試驗結果進行比較，以驗證數值模擬的準確性。

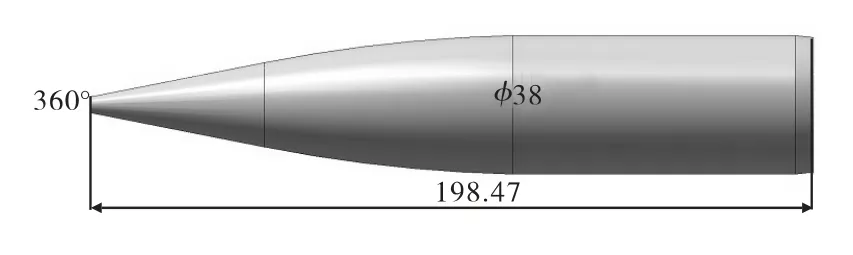
圖1 算例彈丸物理模型

由于彈丸模型相對簡單，故將該彈丸模型建成整體模型，計算域采用圓柱體區域，圓柱體直徑為20倍彈徑，長度為10倍彈長，圓柱體前端距離彈頂為4倍彈長，后端距離彈尾為5倍彈長。采用非結構網格進行計算域網格劃分，網格數為204054個網格，并且在彈頭部、彈頭部與圓柱部連接處和彈尾部分別進行網格加密處理;圖2是彈體表面網格劃分，圖3是放大的計算域的網格劃分。

圖2 算例彈丸表面網格

圖3 算例計算域網格

采用單方程S-A(Spalart-Allmaras)湍流模型(S-A模型比較適合于具有壁面限制的流動問題，常常用在空氣動力學問題中，例如飛行器、翼型等繞流流場分析);計算域外邊界取壓力遠場條件，用給定的自由流馬赫數和靜態條件模擬無限遠處的自由流條件，假設來流為理想氣體，來流攻角為0，來流馬赫數為0.6、0.8、1.0、1.2、1.5、2.0 和 2.5;假設彈丸壁面邊界為無滑移絕熱邊界固壁條件;取遠處前方來流值作為來流初始條件。

將數值模擬得出的阻力系數和文獻[4]里風洞實驗得出來的阻力系數畫成曲線圖，如圖4所示。可見，風洞實驗結果和數值模擬結果近似。但數值計算比試驗結果更加全面，可以直觀地看到彈丸流場參數(壓力、速度、密度等)的分布情況。

圖4 算例阻力系數試驗結果與數值模擬結果對比曲線

1.2 一維彈道修正彈氣動特性分析

不加阻力環以及阻力環加在不同位置的一維彈道修正彈模型方案(彈徑為130mm)分別為圖5～圖8所示，阻力環外露高度相同，安裝位置不同。

圖5 未加阻力環模型(M0)

圖6 阻力環距彈頂0.246L(M1)

圖7 阻力環距彈頂0.309L(M2)

圖8 阻力環距彈頂0.327L(M3)

對4種模型方案零攻角，馬赫數為0.588、0.882、1.176、1.471、1.765、2.059 時的三維繞流流場進行了數值模擬。馬赫數為2.059時，4種模型方案的壓力等值線圖如圖9所示。3種模型相對于無阻力環模型的增阻情況如圖10所示。

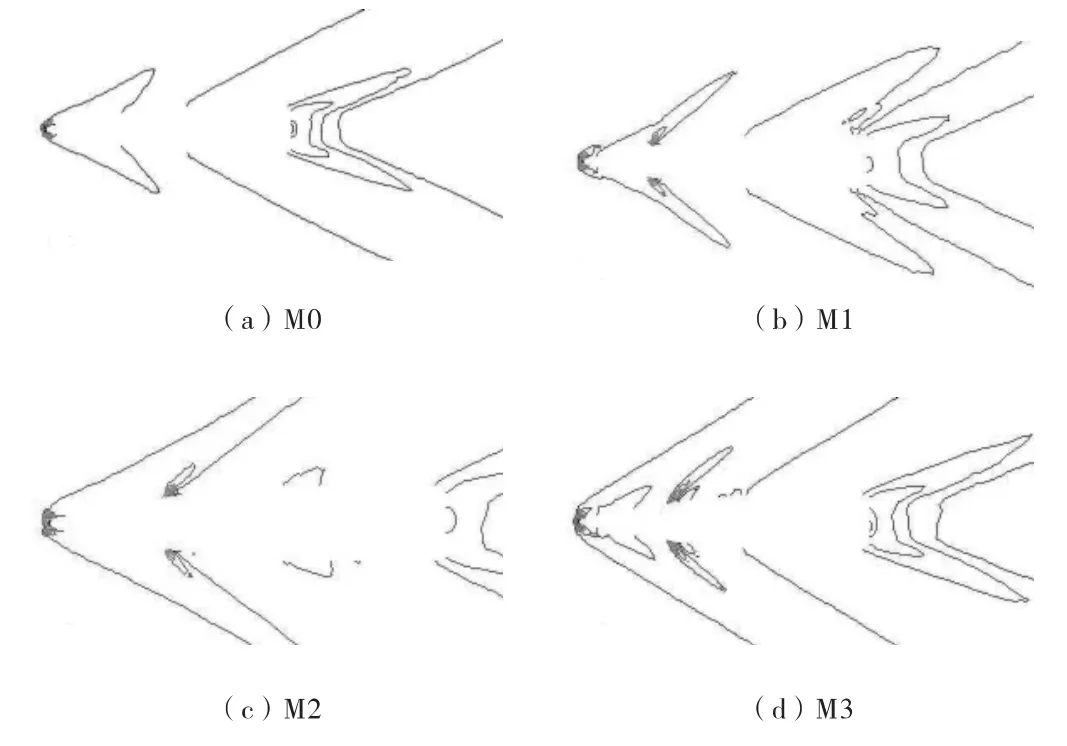
圖9 壓力等值線圖(Ma=2.059)

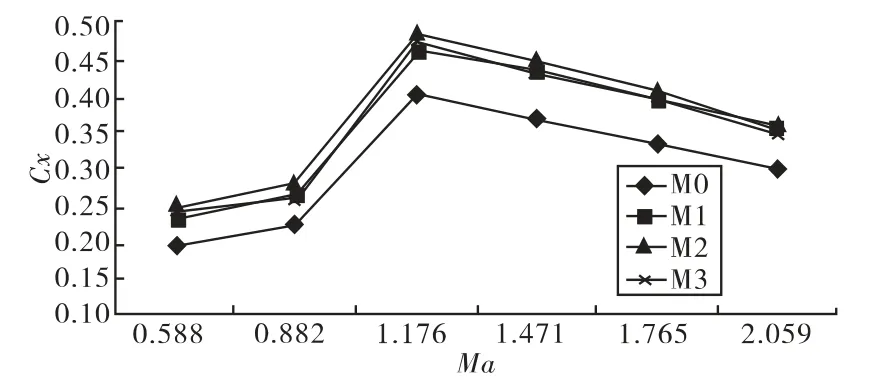
圖10 攻角為零時阻力系數隨馬赫數Ma的變化曲線

從圖中可以看出，阻力環的增加對彈丸外流場有明顯的影響;方案M1的阻力系數比方案 M0增加了約18%，方案 M2的阻力系數比方案 M0增加了約21%。

2 射程修正量計算與分析

2.1 射程修正量計算

一維彈道修正彈的射程修正量ΔX為:

式中:X是阻力環不打開時彈丸的射程，X*是阻力環打開后修正彈的射程。阻力環一經打開就一直持續到彈丸飛行結束。在阻力環結構及發射條件不變的情況下，ΔX取決于阻力環的打開時刻ton。

2.2 不同阻力環模型方案的射程修正能力分析

以修正彈模型M1為例，分析阻力環在不同打開時刻的射程修正量變化。阻力環不打開時，計算初始條件為:射角 θ0=45°，彈丸初速 v0=850m/s，計算得出彈丸最大射程為X=23007m，飛行時間為t=81s，落速為 v=324m/s，彈道傾角 θ= －64.7°。阻力環在不同時刻打開時，以阻力環打開時刻的彈道數據為初始數據，代入修正彈模型M1的阻力系數，運行質點外彈道程序，得到修正彈M1在不同時刻打開阻力環時的修正彈道曲線示意圖如圖11所示。圖中實線為阻力環不打開的彈道曲線，虛線為阻力環在不同時刻打開的修正彈道曲線。從圖中可以看出，阻力環的打開時刻越早，射程修正量越大。采用一維彈道修正彈進行射程修正時，通常選擇在彈道頂點附近打開阻力環修正彈道。

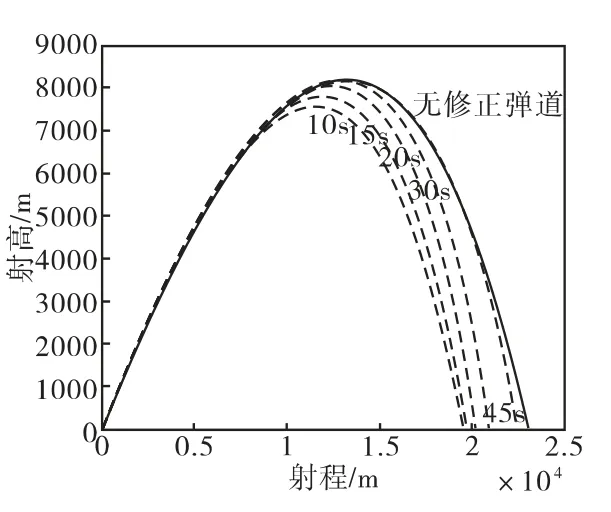
圖11 θ0=45°時，阻力環在不同打開時刻的修正彈道示意圖

以阻力環打開時刻的實測彈道數據為初始數據，代入不同模型方案的阻力系數，運行質點外彈道程序，得到不同阻力環位置的模型方案的射程修正能力隨阻力環打開時刻的變化曲線如圖12所示。

圖12 射程修正百分比隨打開時刻ton的變化曲線

2.3 阻力環打開時刻的計算

阻力環打開時刻的計算方法[5]如圖13所示。

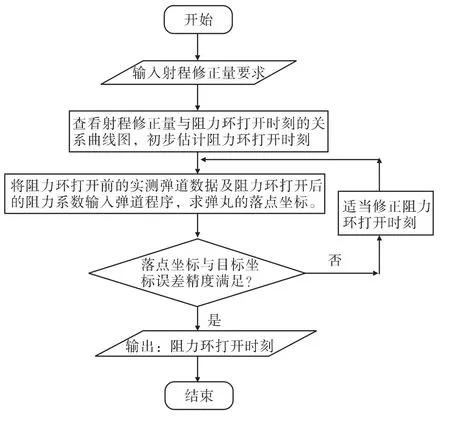
圖13 阻力環打開時刻計算方法

根據射程修正要求，從上述得到的射程修正量ΔX與阻力環打開時刻ton的變化曲線圖中，查出大致的阻力環打開時刻;將阻力環打開前的實測彈道數據及阻力環打開后的阻力參數代入彈道程序，估算彈丸落點坐標，根據與預設彈丸落點的遠近情況，適當修正打開時刻，直到彈丸的落點偏差滿足所需的精度要求，即停止計算。以上計算過程在地面火控計算機中進行，將此結果通過指令傳輸系統發送至彈上的修正機構，修正機構根據此指令控制阻力環的打開動作。

3 結論

文中研究了應用數值模擬方法計算一維彈道修正彈氣動特性的方法，通過典型算例驗證了數值模擬計算模型的可行性，分析了阻力環的安裝對彈丸繞流流場的影響，分析了不同阻力環安裝位置的模型方案的氣動特性。應用自編的質點外彈道計算軟件，以阻力環打開時刻的彈道數據為初始數據，分析了不同模型方案的射程修正能力隨阻力環打開時刻的關系曲線，進一步研究了根據射程修正要求計算阻力環打開時刻的方法。文中研究成果可為一維彈道修正彈的氣動設計和彈道控制提供一定的參考依據。

[1]譚鳳崗.彈道修正彈的概念研究[J].彈箭技術，1998(4):1－10.

[2]趙金強，龍飛，孫航.彈道修正彈綜述[J].制導與引信，2005，26(4):16－19.

[3]蔚微.一維彈道修正彈關鍵技術研究及其實現[D].成都:電子科技大學，2010.

[4]裔萍.一維彈道修正彈的氣動力特性研究[D].南京:南京理工大學，2006.

[5]陶陶，王海川.一維彈道修正彈阻力環修正控制算法研究[J].指揮控制與仿真，2009，31(3):88－93.