迫擊炮彈彈道一致性檢驗與設計探討*

黃成輝，蔣東方，趙星海

(國營9613廠，湖南永州 425000)

0 引言

同一火炮配用多種不同的彈藥，要求通用射表或彈道一致，這是外彈道設計中經常碰到的問題。關于彈道一致性檢驗方法、判據以及槍彈、艦炮等武器系統的彈道一致性研究甚多。而迫擊炮彈飛行軌跡呈拋物線形，近似于真空彈道，外彈道相對簡單，國內外鮮有系統、專一的研究。文中基于彈箭彈道一致性檢驗原理和方法，試圖探討一條適合于迫擊炮彈彈道一致性檢驗與設計控制的途徑。

1 檢驗原理和方法[1]

1.1 檢驗原理

同一火炮同一射擊條件下射擊同一彈種的彈著點散布服從正態分布，射擊不同彈種的正態分布存在差異。按照數理統計的觀點，判斷彈道是否一致，就是判斷兩彈種是否屬于同一母體，檢驗其正態分布的數學期望是否存在顯著性差異。

設在地面坐標系o-xyz中(見圖1)，對比彈和被試彈的彈著點坐標分別為(x0，z0)、(x1，z1)。假設檢驗成立，則認為兩彈彈道一致。式中E系射程或方向概率誤差。

圖1 地面坐標系

1.2 檢驗和試驗方法

彈道一致性檢驗方法分為成組檢驗法和成對交叉檢驗法兩種。在實際工作中，都是采用成對交叉檢驗法，即在同一火炮相同射擊諸元下，采用對比彈與被試彈單發交叉射擊，成對統計彈道差，用t檢驗檢驗其平均值，評定其彈道一致性。

迫擊炮射角為45°～85°，發射裝藥屬于變裝藥，其彈道一致性檢驗試驗一般選取3個裝藥號(最大、最小和中間某裝藥號)，每個裝藥號以2～3個射角(最大、最小和中間某射角)射擊被試彈和對比彈各1 ～3組，每組7 ～ 10發[2]。

2 理論設計方法

彈道一致性設計就是控制被試彈與對比彈的彈道差小于一致性設計控制限，保證被試彈以一定接收概率通過樣本試驗檢驗。一致性設計控制限依賴于一致性界限、概率誤差和一致性接收概率等，是兩彈設計彈道差的允許極限。一致性界限由試驗組數、發數及顯著性水平和概率誤差確定，是試驗檢驗評定彈道一致性的極限判定值。

2.1 試驗組數m、每組試驗發數n以及顯著性水平α 的選取[3]

就迫擊炮彈而言，一般取m=3、n=7。研制前期，因方案多變，一般取m=1、n=7。當要求平均彈道基本一致時，取α=0.01;當要求平均彈道一致時，取 α =0.05。

2.2 一致性界限系數λs[3]

一致性界限系數λs是一致性界限a與概率誤差E的比值，按文獻[3]相關公式解出，計算結果見表1。

2.3 一致性設計控制限系數λsp[3]

一致性設計控制限系數λsp是彈道一致性設計控制限K與概率誤差E的比值，按文獻[3]相關公式解出，計算結果見表1。

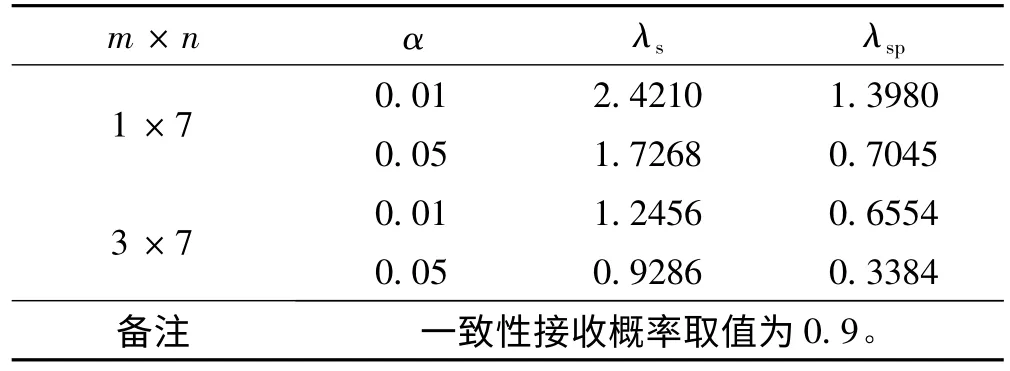
表1 常用 λs、λsp值

2.4 一致性設計控制限K

一致性設計控制限K[3]由下式確定:

2.5 計算彈道差Δ

首先，校核被試彈的飛行穩定性，應符合要求。然后，應用射表，或利用外彈道計算程序、自身阻力系數計算，求出對比彈在不同飛行速度時的阻力系數(或彈形系數)。再估算被試彈的阻力系數(或彈形系數)，應用外彈道計算程序求出其射程。最后，計算兩彈在相同初速、射角下的彈道差Δ。

2.6 結果評定

若Δ≤K，則認為兩彈彈道一致。

3 設計實例

以某型尾翼式82mm迫擊炮新彈設計為例，介紹迫擊炮彈彈道一致性的設計和檢驗過程。82mm新彈(被試彈)與82mm制式彈(對比彈)的外形分別見圖2、圖3，指標要求其母彈平均彈道基本一致。

圖2 新彈外形圖

圖3 對比彈外形圖

新彈內部結構與對比彈差異顯著，彈體外形也有所不同。對比彈為整體式圓柱部，新彈圓柱部由三段組合而成，長度有所增加，對外彈道性能影響較大。為了減少膛內及炮口初始擾動，提高精度，新彈彈頭與前定心部之間設計采用了類似于火箭彈的圓柱部連接方式。

設計時，首先確保新彈的設計膛壓、初速、膛內藥室容積與對比彈相同，彈重在對比彈彈重分級范圍內，配用對比彈的發射裝藥，即保證內彈道一致。其次，在優先保證彈丸裝填、終點效應和最大地面射程及密集度等前提下，力求兩彈幾何外形、尾翼穩定裝置、彈重、質心和赤道轉動慣量等彈丸特征數基本一致，盡量消除影響彈道一致性的不利因素，或減輕其影響程度。

3.1 判斷新彈的飛行穩定性[4]

根據彈丸設計理論，應用特征數計算程序、АНИИ法等，求出有關參數:赤道轉動慣量 Jy=0.0630kg·m2，擺動波長λ =46.5m，靜態穩定儲備量B=16.40%。根據穩定性判定準則，因為靜態穩定儲備量B介于15% ～20% 之間，且將點(lgJy，λ)畫在現有迫擊炮彈飛行穩定性曲線圖上，該點處于穩定區域內，表明新彈飛行穩定性滿足要求。

3.2 計算對比彈的標準射程

依據射表(或實測值、彈丸自身阻力系數)，求得對比彈各裝藥號不同射角的標準射程，見表2，自身阻力系數值見表3、圖4。

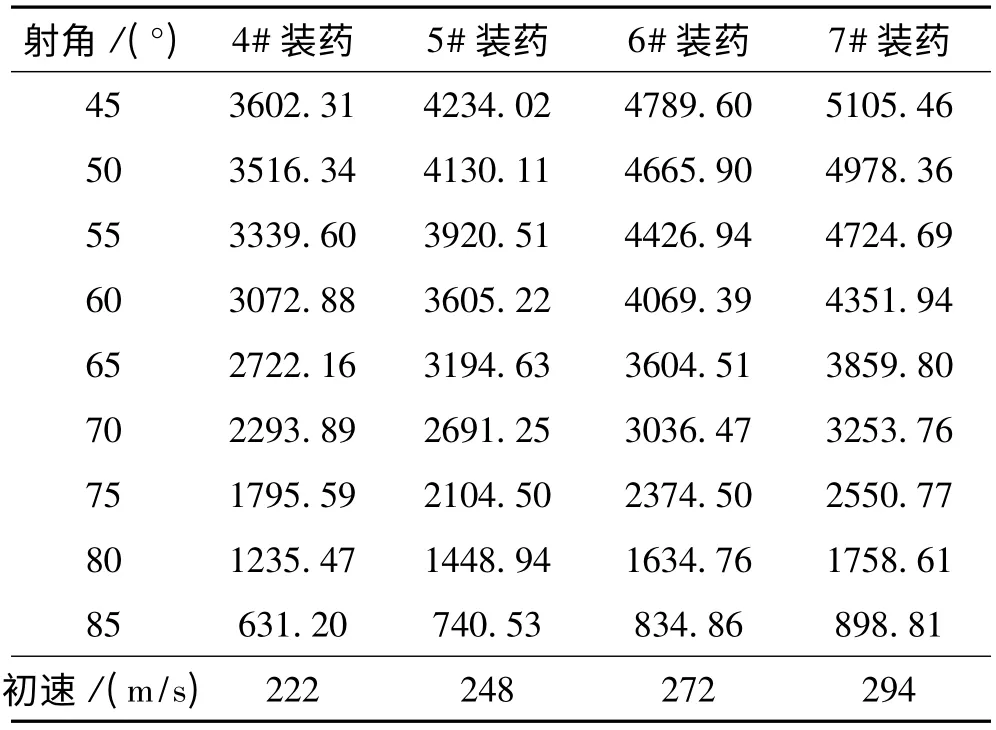
表2 對比彈標準射程 m

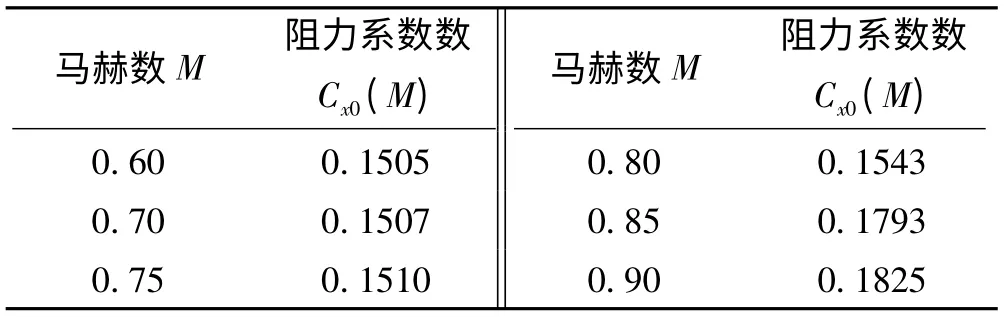
表3 對比彈自身阻力系數Cx0(M)

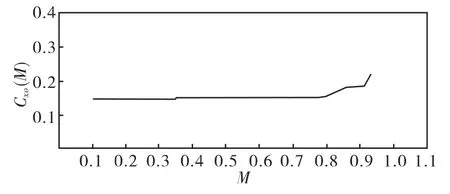
圖4 對比自身阻力系數Cx0(M)曲線

3.3 推算對比彈的等效彈形系數

依據表2，按照文獻[4]外彈道計算程序，進行符合性計算，可反向推算出對比彈對應于43年阻力定律的彈形系數，即等效彈形系數，見表4。根據實踐經驗，引入等效彈形系數概念，可以簡化計算，對于迫擊炮彈的設計計算符合性較好。

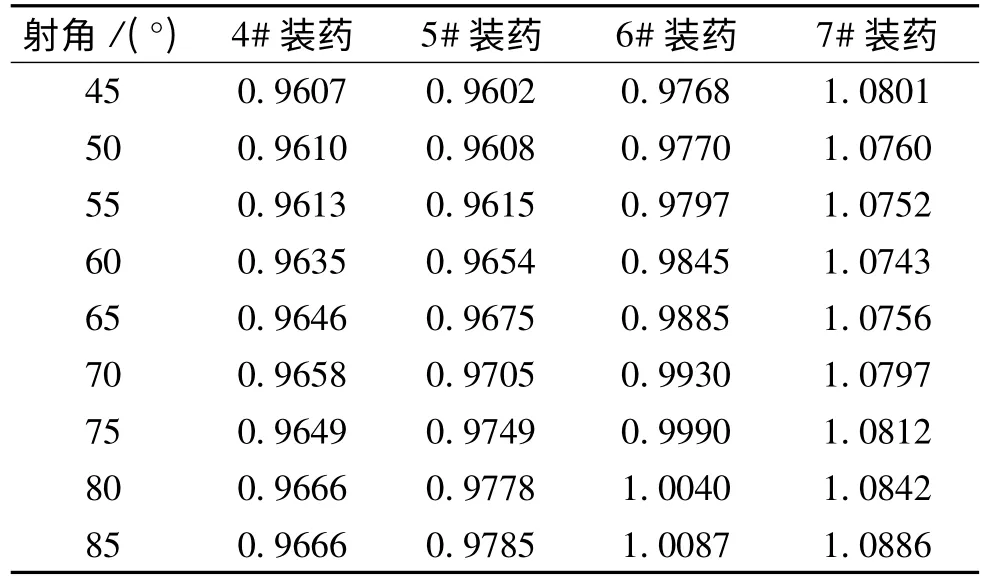
表4 對比彈的等效彈形系數i'43d

3.4 計算一致性設計控制限

對比彈有4個發射裝藥號(4#～7#)，現選取4#、7#裝藥進行計算。根據歷史試驗數據，統計得到對比彈射程和方向的概率誤差Ex、Ez，見表5。繪制E － θ曲線(描述概率誤差隨射角變化的趨勢)，見圖5、圖6。

表5 對比彈概率誤差Ex、Ez m

因為戰技指標要求兩彈彈道基本一致，可取α=0.01，λsp=0.6554。將 λsp、Ex、Ez代入式(1)，計算出新彈射程和方向的一致性設計控制限Kx、Kz，見表6。繪制K-θ曲線(描述一致性設計控制限隨射角變化的趨勢)，見圖 7、圖 8。

表6 新彈一致性設計控制限Kx、Kz m

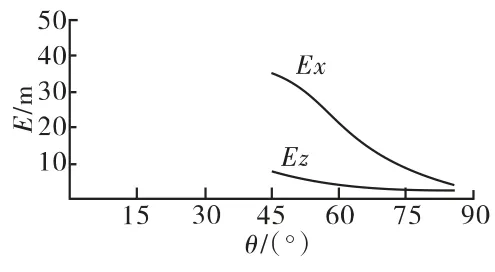
圖5 對比彈4#裝藥E-θ 曲線

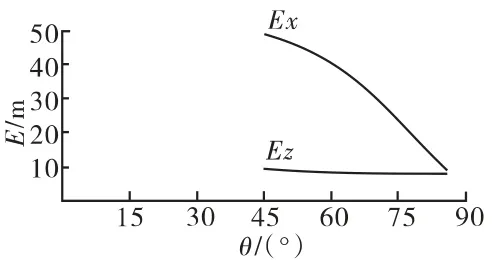
圖6 對比彈7#裝藥E-θ 曲線

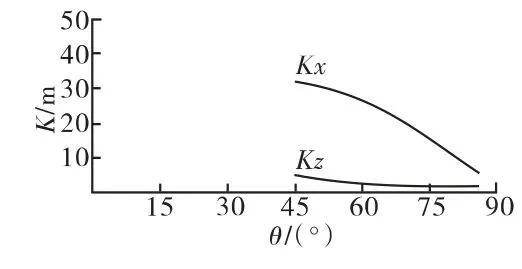
圖7 新彈4#裝藥K-θ 曲線

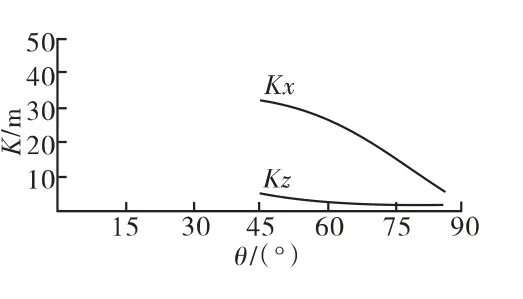
圖8 新彈7#裝藥K-θ 曲線

3.5 計算彈道差

a.估算新彈的阻力系數:新彈與對比彈幾何外形相似，采用相同的引信和尾翼穩定裝置，主要的阻力變化因素來自彈頭部，因此其阻力系數可按式(2)估算(若有其它阻力變化，可在公式中疊加)。

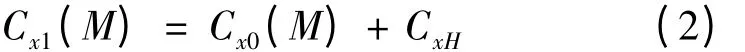
根據文獻[5]，定心部引起的阻力系數CxH按式(3)計算，并查圖取ΔCxH值。

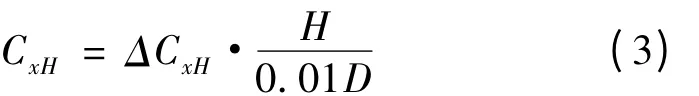
已知設計值H=1mm，D=82mm，代入式(2)、式(3)，計算出新彈的阻力系數，見表7。

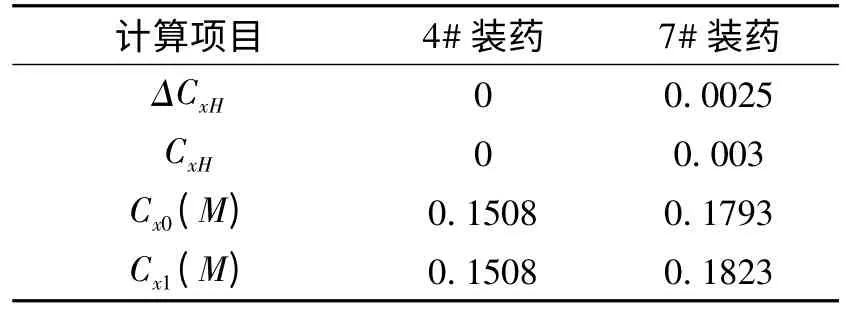
表7 新彈的阻力系數Cx1(M)計算值

b.推算新彈的等效彈形系數:根據外道彈學中關于彈形系數的定義可知:

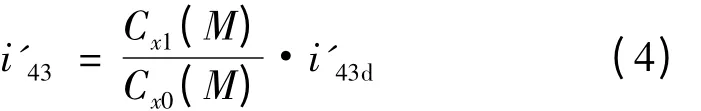
Cx0(M)、i'43d、Cx1(M)分別查表 3、表 4、表 7 取值，代入式(4)，計算出新彈的等效彈形系數 i'43，見表8。

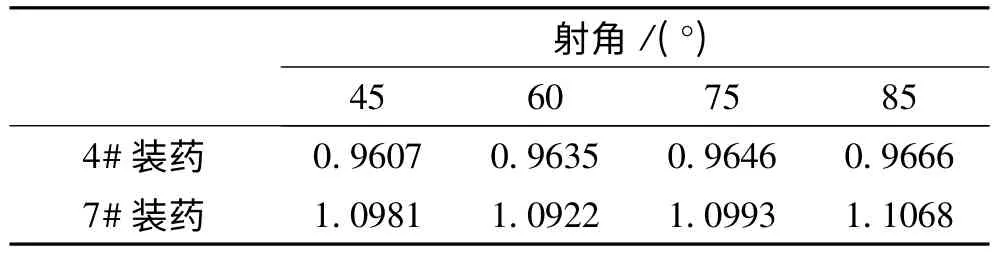
表8 新彈的等效彈形系數i'43

c.估算平均彈道差:將初速、射角、彈重、等效彈形系數等代入外彈道計算程序，分別計算新彈和對比彈的平均射程 x－1、x－0以及平均彈道差 Δx－，見表 9、表10。繪制 Δx－-θ曲線(平均彈道差隨射角變化的趨勢)，見圖 9、圖 10。

表9 新彈4#裝藥彈道一致性理論設計數據

表10 新彈7#裝藥彈道一致性理論設計數據

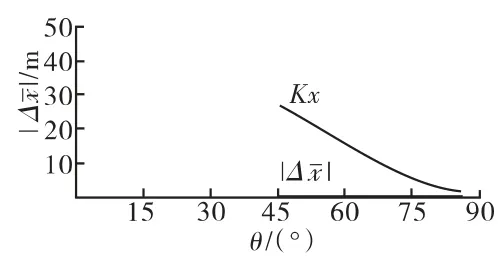
圖9 新彈4#裝藥K-θ 曲線

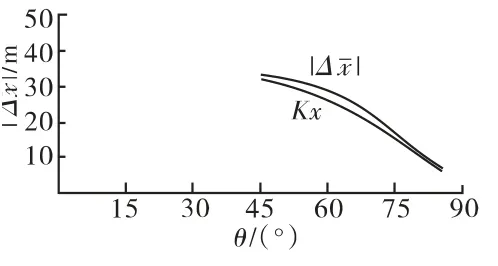
圖10 新彈7#裝藥K-θ 曲線

3.6 初步設計結論

因為迫擊炮彈的方向偏差較小，通常能滿足要求，文中計算略。

由圖9可知:4#裝藥的設計彈道差小于一致性設計控制限，可滿足彈道一致性要求;同理，計算5#、6#裝藥設計彈道差，也能滿足要求。

由圖10可知:7#裝藥的設計彈道差大于一致性設計控制限，不滿足彈道一致性要求。

3.7 改進設計

根據表10可知:新彈7#裝藥最大設計射程偏近，導致設計彈道差偏大。分析認為，主要原因是彈頭部阻力較大。現將彈頭圓柱部與定心部半徑差H=1mm改為H=0.4mm，再按3.5節計算、制表并制圖。經計算，4#、5#和6#裝藥滿足要求，7#裝藥也滿足要求，7#裝藥的計算結果見表11、圖11。

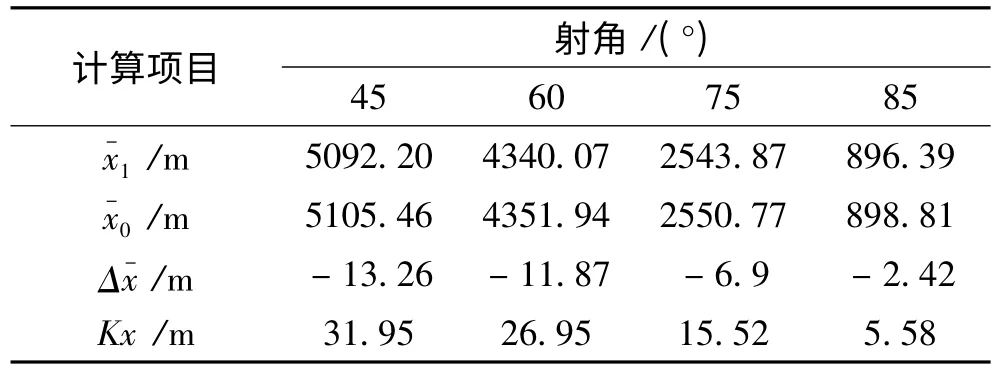
表11 新彈7#裝藥彈道一致性理論設計數據

4 試驗驗證

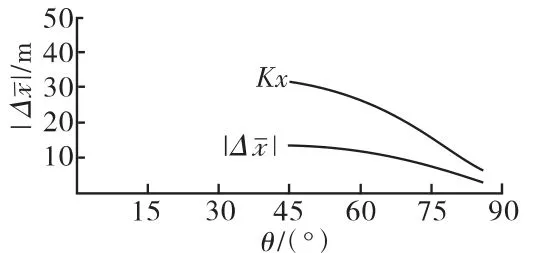
圖11 7#裝藥曲線

以 7#裝藥、45°射角，結合最大地面射程及密集度試驗進行了彈道一致性摸底試驗，按文獻[2]成對交叉檢驗要求進行試驗和數據處理，見表 12、表 13。

由表13可知:對應于7#裝藥45°射角，新彈與對比彈彈道一致。7#裝藥其它射角和裝藥號的彈道一致性，在后續研制階段得到驗證，符合要求。

表12 射程和方向試驗數據

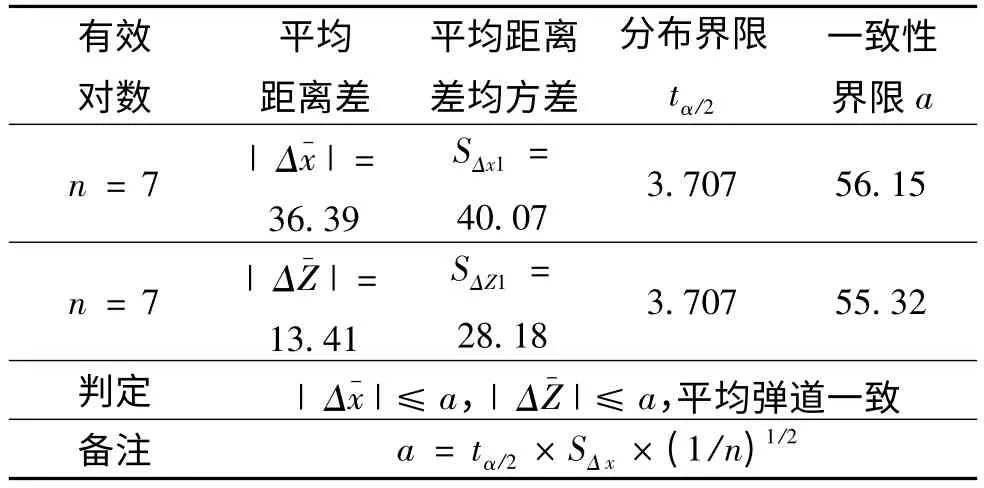
表13 試驗數據處理結果

5 結論

針對迫擊炮彈，基于彈箭彈道一致性檢驗原理和方法，在設計保證內彈道一致的條件下，運用成對交叉檢驗法，通過外彈道計算，使新彈與對比彈的設計彈道差小于一致性設計控制限，理論上可以保證兩彈彈道一致。在設計例證中，引入等效彈形系數的外彈道計算方法簡單有效，符合性好。試驗驗證結果表明，所闡述的設計控制方法合理有效，有一定的實用價值。

[1]王中原，張領科.彈箭通用射表及彈道一致性檢驗方法[M].北京:科學出版社，2008.

[2]GJB 4225－2001榴彈定型試驗規程[S].北京:總裝備部軍標出版發行部，2001.

[3]WJ 2144－1993彈道一致性設計與檢驗評定[S].北京:中國兵器標準化研究所，1993.

[4]魏惠之，朱鶴松，汪東暉，等.彈丸設計理論[M].北京:國防工業出版社，1985.

[5]臧國才，李樹常.彈箭空氣動力學[M].北京:兵器工業出版社，1989.