模糊自適應(yīng)調(diào)整趨近律的導(dǎo)彈姿態(tài)滑模控制系統(tǒng)設(shè)計(jì)*

唐意東，李小兵，喬朋朋

(空軍工程大學(xué)防空反導(dǎo)學(xué)院，西安 710051)

0 引言

利用變結(jié)構(gòu)控制響應(yīng)快速、對參數(shù)變化和擾動(dòng)不靈敏的特點(diǎn)，可以實(shí)現(xiàn)對系統(tǒng)較好的控制。但是，在控制過程中，系統(tǒng)狀態(tài)及控制量的變化不可能瞬間發(fā)生，即不可能產(chǎn)生連續(xù)的變化。由于慣性引起滯后的原因，切換函數(shù)在不斷切換的過程中必然會(huì)產(chǎn)生抖動(dòng)。對于如何削弱滑模變結(jié)構(gòu)控制中的抖振，文獻(xiàn)[1]采用連續(xù)化法，用飽和型切換代替繼電型切換，即所謂的“邊界層”法。但是在引入飽和型切換后，系統(tǒng)已經(jīng)不是變結(jié)構(gòu)系統(tǒng)，自然也就失去了變結(jié)構(gòu)控制系統(tǒng)最大的優(yōu)勢——對參數(shù)攝動(dòng)和擾動(dòng)的魯棒性。而且對于非線性系統(tǒng)，即使在邊界層內(nèi)同樣存在抖動(dòng)[4]。文獻(xiàn)[2]則用飽和非線性函數(shù)代替符號函數(shù)，式中δ的選擇對去抖有較大影響。這種滑模變結(jié)構(gòu)控制方法，是通過確定δ的值，在犧牲了一定動(dòng)態(tài)品質(zhì)的前提下，較好的實(shí)現(xiàn)對系統(tǒng)抖振的削弱。文獻(xiàn)[3]設(shè)計(jì)一種最終滑動(dòng)模態(tài)變結(jié)構(gòu)控制系統(tǒng)，在受到擾動(dòng)的時(shí)候需要6s的過渡時(shí)間，這對于工作時(shí)長在60s左右的某型地空導(dǎo)彈來說顯然是不可接受的。對地空導(dǎo)彈這一類需要在不確定環(huán)境下工作，對快速性和魯棒性都有著較高要求的系統(tǒng)來說，尋找一種可以兼顧兩方面性能的控制方法是有實(shí)際意義的。

針對上述情況，文中引入李士勇提出的將模糊控制與常規(guī)滑模變結(jié)構(gòu)控制結(jié)合的控制方法，給出了一種基于模糊自適應(yīng)調(diào)節(jié)的滑模變結(jié)構(gòu)控制律，保證了系統(tǒng)的快速收斂性和對外部擾動(dòng)的魯棒性。利用模糊控制的柔滑控制信號，有效的削弱了滑模變結(jié)構(gòu)控制過程中產(chǎn)生的抖振。最后，將這種方法應(yīng)用于某型防空導(dǎo)彈的姿態(tài)控制系統(tǒng)，驗(yàn)證了該方法的有效性。

1 導(dǎo)彈姿態(tài)控制模型建立

彈體環(huán)節(jié)的運(yùn)動(dòng)微分方程一般講應(yīng)為非線性、變系數(shù)、三維聯(lián)立微分方程組。但是，地空導(dǎo)彈在許多場合是在鉛垂平面或者傾斜平面內(nèi)飛行。因此，可以考慮短周期內(nèi)導(dǎo)彈特征點(diǎn)工作狀態(tài)[6]，利用小擾動(dòng)假定、結(jié)構(gòu)參數(shù)連續(xù)變化假定和固化系數(shù)法，得到有側(cè)滑無傾斜水平面導(dǎo)彈運(yùn)動(dòng)微分方程:

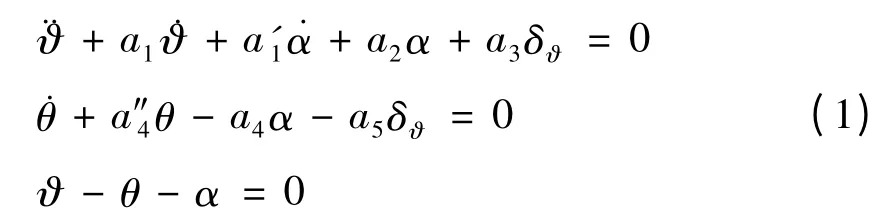
方程(1)中a'1表示氣流下洗延遲對彈體轉(zhuǎn)動(dòng)的影響，其值遠(yuǎn)比a1、a2小，故可以忽略。同時(shí)忽略重力系數(shù)a″4的影響，根據(jù)理想操縱關(guān)系ε=0得? =α。則可以得到導(dǎo)彈運(yùn)動(dòng)狀態(tài)方程:

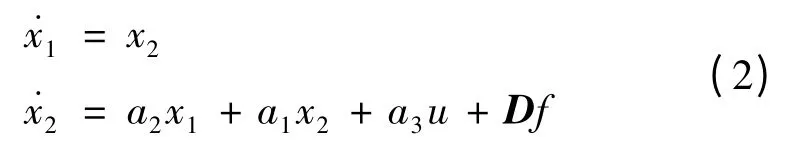
式中:u為俯仰舵偏角δ?，f為外部干擾，‖f‖ ＜F為有界干擾。

2 控制器設(shè)計(jì)

2.1 滑模變結(jié)構(gòu)控制器設(shè)計(jì)

由方程(2)可得系統(tǒng)狀態(tài)方程為:

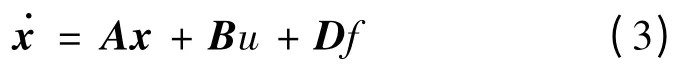
切換函數(shù)s=Cx，C= [c，1]。運(yùn)用任置滑動(dòng)模態(tài)特征向量的方法來確定C陣。由等效控制:

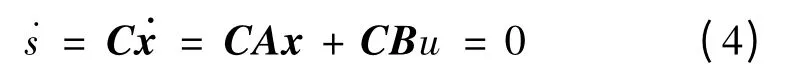
可得u=(CB)－1CAx，則滑動(dòng)模態(tài)方程為:

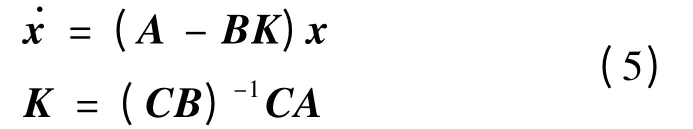
滑動(dòng)模態(tài)發(fā)生于Ker(C)=N(C)之內(nèi)。給定λi(i=1，2，...，n)為滑動(dòng)模態(tài)的特征根。由

可解得c，即得C陣。

選取指數(shù)趨近律:

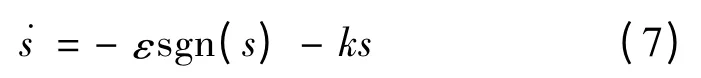
式中ε的取值決定了到達(dá)滑動(dòng)模態(tài)的速率和抖振程度。由式(7)可得控制為:

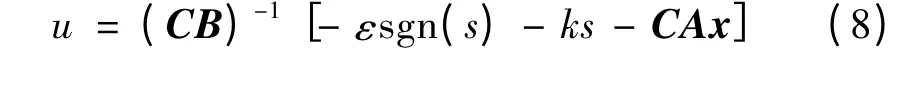
2.2 模糊控制器設(shè)計(jì)

定義模糊子集{NB，NM，NS，ZO，PS，PM，PB}，根據(jù)模糊控制原理，定義s和˙s為模糊控制器的輸入，fs為模糊控制器的輸出，其論域?yàn)?

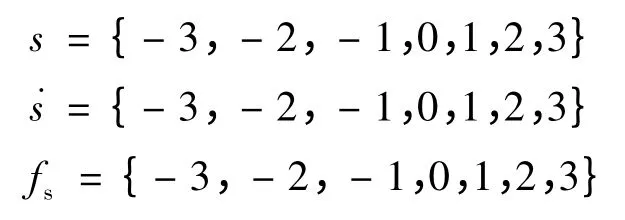
圖1 s，和fs的隸屬函數(shù)

模糊控制規(guī)則如下:

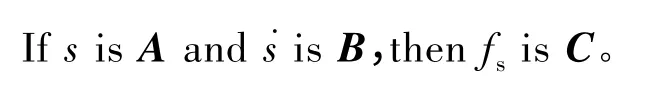
在力圖滿足不等式s˙s＜0的條件下設(shè)計(jì)控制律使得滑動(dòng)模態(tài)有較快的到達(dá)速率，又要在接近滑模面時(shí)減小速率，削弱干擾。所獲得的控制規(guī)則見表1。

表1 模糊控制規(guī)則表

用Ri1·Ri2表示一條語句所確定的模糊關(guān)系，可以算出模糊控制量

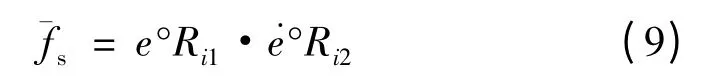
同理可以根據(jù)其余各條語句得到模糊控制量ˉfs，，控制量的模糊集合可以表示為:

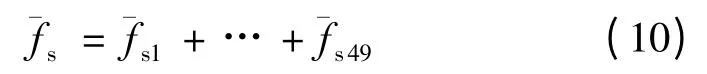
非模糊化過程采用MIN-MAX-重心法，其實(shí)質(zhì)是加權(quán)平均法。調(diào)整加權(quán)系數(shù)可以改善系統(tǒng)的響應(yīng)特性，即調(diào)整各論域內(nèi)元素對模糊語言變量的隸屬度。

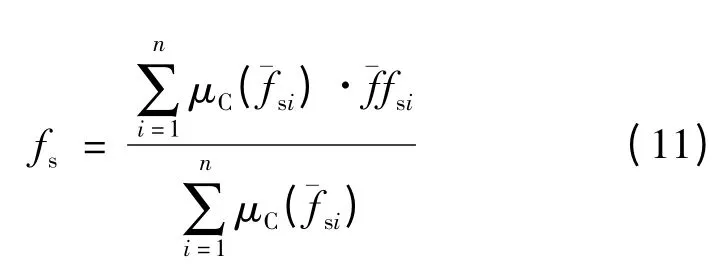
2.3 抗攝動(dòng)及干擾能力分析

系統(tǒng)(3)受干擾和參數(shù)攝動(dòng)情況。令˙s=C˙x=C(A+ΔA)x+CBu+CDf=0，設(shè)CB為非奇異陣，解出等效控制:

代入方程(3)得到描述滑動(dòng)模態(tài)的運(yùn)動(dòng)微分方程:

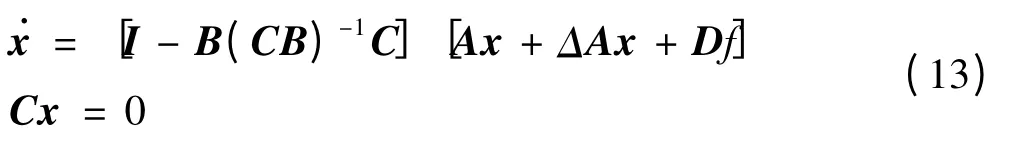
當(dāng)[I－B(CB)－1C]Df=0時(shí)，干擾f將不會(huì)對滑動(dòng)模態(tài)發(fā)生作用。因此滑動(dòng)模態(tài)不受干擾f影響的充分必要條件為[4]:

當(dāng)[I－B(CB)－1C]ΔAx=0時(shí)，參數(shù)攝動(dòng)ΔA將不會(huì)影響到滑動(dòng)模態(tài)。因此不變性成立的充分條件為:

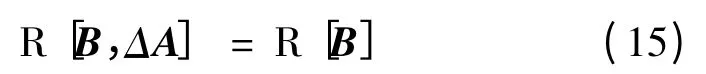
3 仿真及結(jié)果分析

根據(jù)設(shè)計(jì)的控制律，以某型地空導(dǎo)彈俯仰通道姿態(tài)控制系統(tǒng)為例進(jìn)行仿真研究，取參數(shù)q=97568，s=0.2552，l=0.57，v=400，Jy=3996，g=9.81，=－0.18=－0.28，=－128，輸入信號為正弦疊加信號，有界干擾f≤0.01。

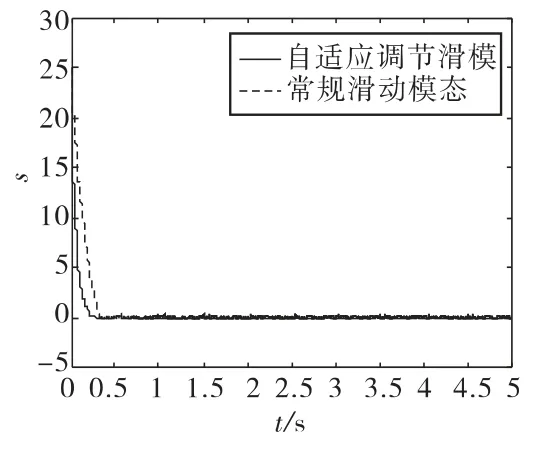
圖2 滑動(dòng)模態(tài)變化曲線

圖2 為滑動(dòng)模態(tài)在到達(dá)切換面過程中的變化曲線，可以看到，模糊自適應(yīng)調(diào)劑的滑模變結(jié)構(gòu)控制過程中，滑動(dòng)模態(tài)能夠更快的到達(dá)切換面，并且能夠有效的削弱抖振。圖3和圖4分別為模糊自適應(yīng)調(diào)節(jié)滑模變結(jié)構(gòu)控制量和常規(guī)滑模變結(jié)構(gòu)控制量的變化曲線，由于輸入是正弦疊加信號，因此控制量周期性變化。同樣，模糊自適應(yīng)滑模變結(jié)構(gòu)控制能夠有效削弱控制量的抖振。圖5和圖6分別為誤差e和誤差變化率˙e相軌跡圖和局部放大圖，可以看到，模糊自適應(yīng)滑模變結(jié)構(gòu)控制的相軌跡以較小的角度平滑的接近切換面。圖7和圖8分別為對正弦疊加信號的跟蹤誤差及其局部放大圖，可以看到誤差在t=0.35s是收斂為零，說明系統(tǒng)穩(wěn)定，收斂時(shí)間可控且有限。仿真結(jié)果表明，基于模糊自適應(yīng)調(diào)節(jié)的滑模變

圖3 自適應(yīng)調(diào)節(jié)滑模變結(jié)構(gòu)控制量變化曲線

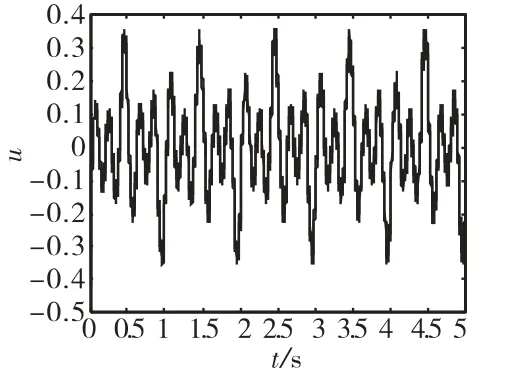
圖4 常規(guī)滑模變結(jié)構(gòu)控制量變化

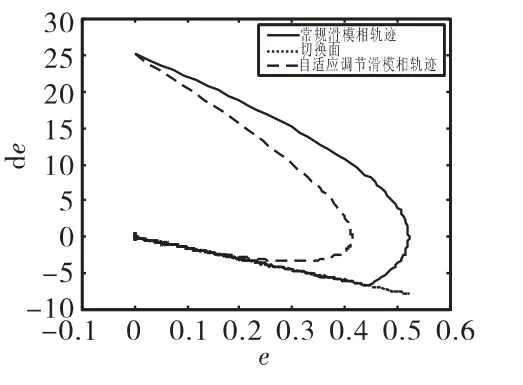
圖5 相軌跡

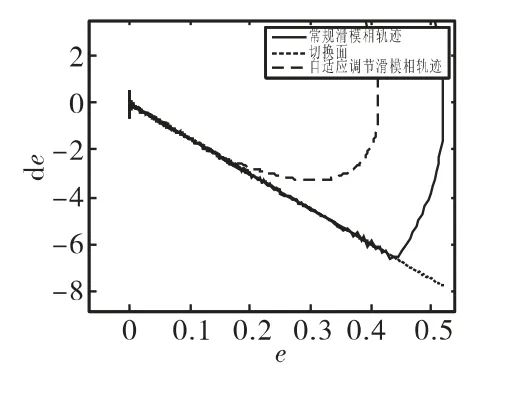
圖6 相軌跡局部放大圖

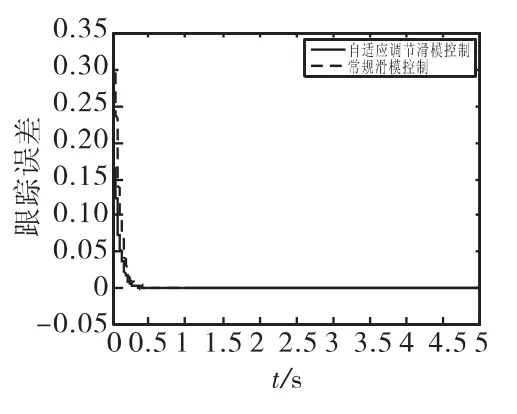
圖7 俯仰角?位置跟蹤

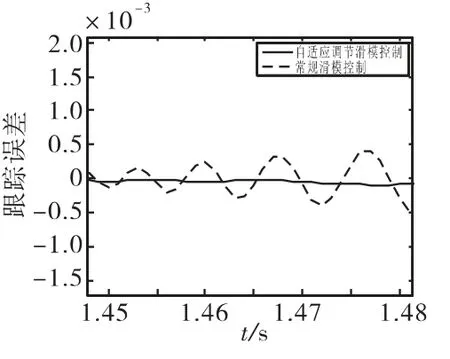
圖8 俯仰角?位置跟蹤局部放大圖

結(jié)構(gòu)控制能夠使導(dǎo)彈穩(wěn)定可靠的對輸入信號實(shí)現(xiàn)跟蹤，并且能夠在保持常規(guī)滑模變結(jié)構(gòu)控制魯棒性的同時(shí)，有效削弱滑模變結(jié)構(gòu)控制產(chǎn)生的抖振。

4 結(jié)論

通過分析傳統(tǒng)滑模控制的特點(diǎn)，考慮系統(tǒng)外部有界干擾和參數(shù)攝動(dòng)，將模糊控制的相關(guān)理論與傳統(tǒng)滑模變結(jié)構(gòu)控制相結(jié)合，設(shè)計(jì)了一種基于模糊自適應(yīng)調(diào)節(jié)的滑模控制方法。能夠保證系統(tǒng)的快速性和魯棒性，優(yōu)于常規(guī)滑模變結(jié)構(gòu)控制。文中對系統(tǒng)進(jìn)行了小擾動(dòng)假設(shè)和固定系數(shù)處理，對于充分考慮時(shí)變和不確定系統(tǒng)的情況可以引入一類自適應(yīng)辨識(shí)方法對參數(shù)進(jìn)行在線辨識(shí)[8]。

[1]趙宏戰(zhàn)，周軍.防空導(dǎo)彈姿態(tài)控制系統(tǒng)終態(tài)滑模變結(jié)構(gòu)設(shè)計(jì)[J].計(jì)算機(jī)仿真，2009，26(2):73 －76.

[2]胡龍兵，李言俊.一種改進(jìn)的變結(jié)構(gòu)制導(dǎo)律的設(shè)計(jì)與仿真[J].火力與指揮控制，2010，35(9):193 －194.

[3]戚京鋒，周鳳岐.最終滑動(dòng)模態(tài)變結(jié)構(gòu)導(dǎo)彈控制系統(tǒng)設(shè)計(jì)[J].彈箭與制導(dǎo)學(xué)報(bào)，2004，24(3):273 －275.

[4]高為炳.變結(jié)構(gòu)控制理論基礎(chǔ)[M].北京:中國科學(xué)技術(shù)出版社，1990.

[5]張翼飛，楊輝，鄧方林.二階系統(tǒng)模糊變結(jié)構(gòu)控制器設(shè)計(jì)及穩(wěn)定性分析[J].系統(tǒng)工程與電子技術(shù)，2005，27(2):312－315.

[6]陳佳實(shí).導(dǎo)彈制導(dǎo)和控制系統(tǒng)的分析與設(shè)計(jì)[M].北京:宇航出版社，1989.

[7]劉金琨.滑模變結(jié)構(gòu)控制MATLAB仿真[M].2版.北京:清華大學(xué)出版社，2012.

[8]韓曾晉.自適應(yīng)控制[M].北京:清華大學(xué)出版社，1995.