非等間距無偏GM（1，1）模型在建筑沉降預測中的應用

曹 昶，樊重俊

（上海理工大學 管理學院，上海 200093）

隨著土地資源逐漸減少與人口增長之間矛盾日益突出，高層及超高層建筑越來越多，建筑沉降問題也越來越受到人們的重視。在建筑工程施工中，由于地質條件不同和結構荷載變化懸殊等原因，容易產生建筑工程的不均勻沉降。建筑沉降問題直接影響著工程質量和建設周期，而且關系人們的財產安全和生命安全。科學、準確、及時地預測建筑沉降，對建筑工程的施工和運營管理極為重要［1－2］。建筑沉降的影響因素繁多，有地質條件、結構荷載、施工環境、天氣情況等，其中許多因素是不確定的，因此建筑沉降的預測過程是一個灰色系統。目前，常用的沉降預測方法有回歸分析、確定函數法、時間序列法等，但是這些方法都要求有大量樣本［3］。在沉降或變形預測初期或者觀測頻次較低的情況下無法獲得很多數據，因此適合采用所需樣本數據少、計算簡單方便的GM（1，1）模型進行預測［4］。

GM（1，1）模型是以等間距數列為基礎的，但在實際的工程測量中建筑沉降觀測時間間距往往是非等間距的［5］。本文將非等間距數列經過一定的處理，轉化為等間距數列。最后使用無偏GM（1，1）模型對處理后的數據進行建模預測。通過工程實例，表明此方法具有較高的預測精度。

1 非等間距數列的變換

設非等間距數列X（0）＝｛x（0）（1），x（0）（2），…，x（0）（n）｝，將其轉換為等間距數列的步驟如下：

1）計算各觀測周期距首次周期的時間間隔：

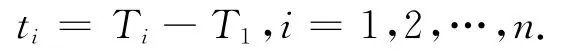
其中，Ti為各期的原始觀測時間。

2）求平均時間間隔［6］：

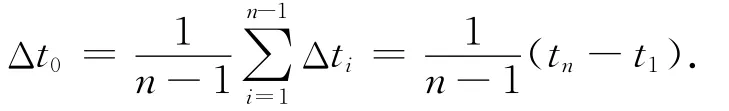
3）求各期的時距ti與平均時距Δt0的單位時間差系數：

4）求各期的總差值：

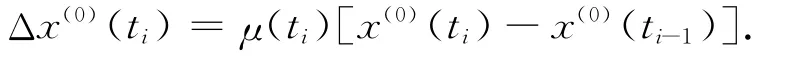
其中，x（0）（ti）為ti的原始觀測值。

5）計算等間距點的灰數值：

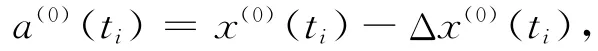
得到等間距數列：

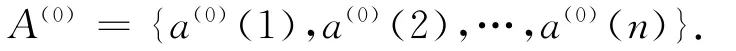
2 基于非等間距的無偏GM（1，1）模型

設 原 始 數 列X（0）＝｛x（0）（1），x（0）（2），…，x（0）（n）｝，且x（0）（k）≥0（k＝1，2，…，n），傳統GM（1，1）建模步驟［7］：

1）對原始數列X（0）作一次累加生成：

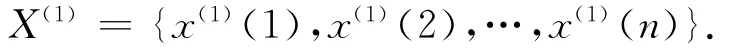
2）對數列X（1）作緊鄰均值生成。令z（1）（k）＝0.5［x（1）（k）＋x（1）（k－1）］得

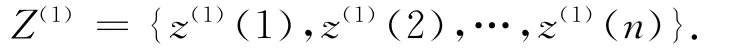
3）由一階累加生成序列X（1）建立GM（1，1）模型，對應的白化微分方程為

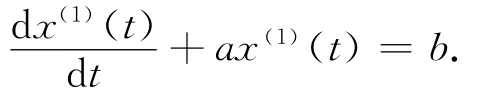
4）在初始條件在x（1）（1）＝x（0）（1），上述方程的離散解為

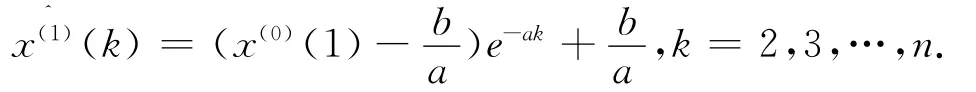
參數列β＝（a，b）T由最小二乘法確定

其中

5）還 原 求 出X（0）的 模 擬 值。由得

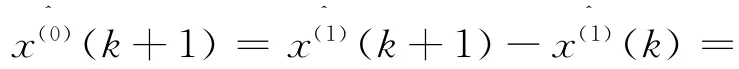
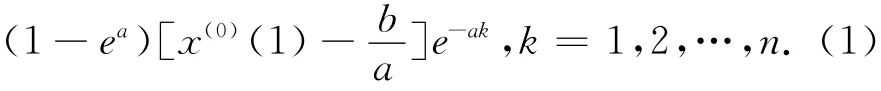
若原始數列為嚴格的指數序列，即：

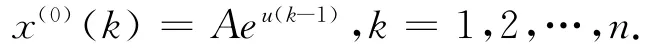
按照GM（1，1）建模過程得

最終預測值為

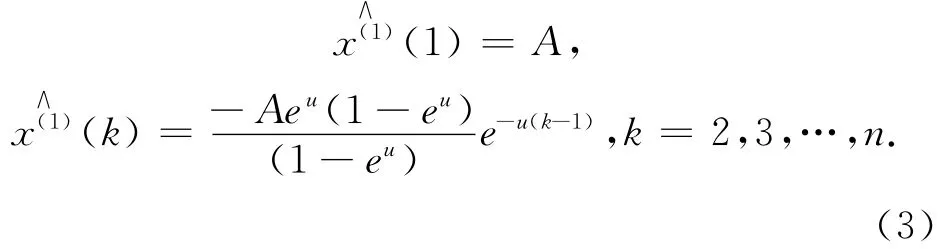
比較式（1）和式（3）可見兩式存在差異，傳統GM（1，1）模型存在固有偏差。由式（2）得

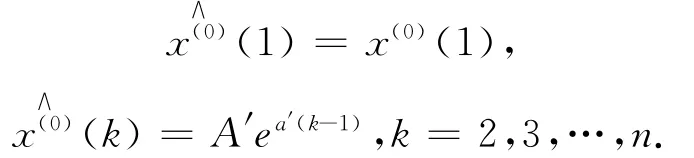
6）將其還原為非等間距中有關t的響應函數：

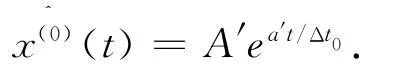
無偏差GM（1，1）模型本身不存在固有偏差，消除了在原始數據序列增長過快導致失效的現象，拓廣GM（1，1）模型的使用范圍［8］。

3 實例應用

某建筑工程為確保施工安全，在施工過程中進行了沉降監測。表1為其中一個監測點的部分觀測數據。

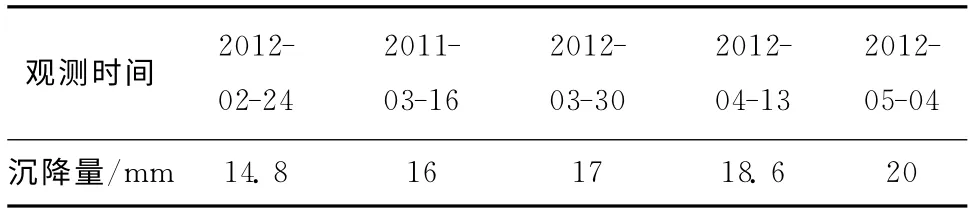
表1 某沉降點實測數據

1）計算各觀測周期距首次周期的時間間隔（以d為單位）：

2）求平均時間間隔：

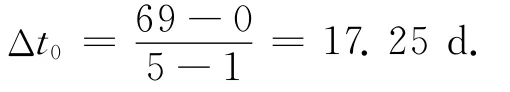
3）求各期的間距ti與平均時距Δt0的單位時間差系數：

4）計算各期的總差值：

5）計算等間距點的灰數值：

6）對數列A（0）按照GM（1，1）模型建模得：

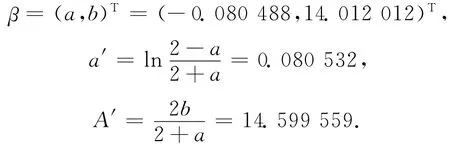
7）還原為非等間距數列有關t的響應函數：

4 模型比較及檢驗

表2為傳統GM（1，1）模型和無偏灰色模型模擬精度的比較。

表2 模型精度比較

1）平均相對誤差為

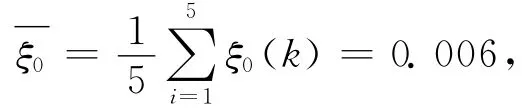
所以預測精度為一級。

2）后驗差檢驗［9］為

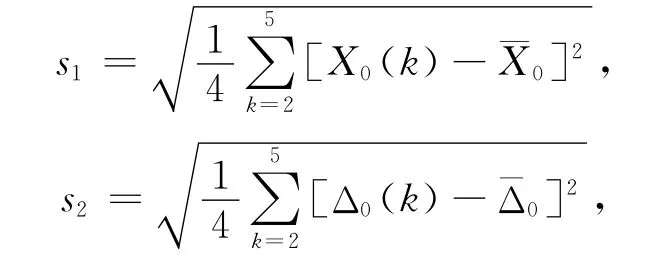
3）小誤差概率［10］為

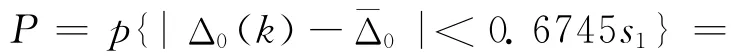
根據模型預測后續某些觀測時間的沉降量，并與實際測量值比較，兩種模型預測效果比較見表3。

表3 模型預測效果比較

5 結束語

從表2和表3中可以看出，基于非等間距的無偏灰色模型模擬精度更高，預測效果更好。本文將非等間距數列轉化為等間距數列，并運用無偏GM（1，1）模型進行預測。在具體的工程沉降預測中，將非等間距實測數據轉化為等時距數列，并給出了無偏GM（1，1）模型的具體方法。結果表明，基于非等間距的無偏GM（1，1）模型具有計算量小、需要原始數據少、精度高等優勢，完全能滿足建筑沉降預測的需要。在建筑物施工過程中應用該建筑沉降模型進行預測，指導合理的施工工序，加強全過程監控。

［1］單瑞，獨知行，劉焱雄.基于等時距數據序列的高層建筑沉降預測［J］.測繪科學，2010，35（3）：100－102.

［2］張健雄，蔣金豹，張建霞.高層建筑沉降監測與灰色預測［J］.測繪科學，2007，32（4）：56－59.

［3］孫思忠，王利民.應用灰色理論對高層建筑沉降變形進行預測的研究［J］.建筑科學，2007，23（11）：13－15.

［4］朱華吉，馬少娟.非等時空距GM（1，1）模型在建筑物沉降預測中的應用［J］.測繪工程，2001，10（4）：39－41.

［5］黃聲享，李志成.工程建筑沉降預測的非等間距灰色建模［J］.地理空間信息，2004，2（1）：41－43.

［6］唐萬梅，向長合.基于二次插值的GM（1，1）模型預測方法的改進［J］.中國管理科學，2006，14（6）：109－112.

［7］吉培榮，黃巍松，胡翔勇.無偏灰色預測模型［J］.系統工程與電子技術，2000，22（6）：6－7.

［8］王錚，和瑩.灰色系統建模方法的理論困難及其克服［J］.系統工程理論與實踐，1990，10（5）：17－22.

［9］劉思峰，黨耀國，方志耕，等.灰色系統理論及應用［M］.北京：科學出版社，2012.

［10］孫澤信，龐逸群，黃騰.改進的灰色模型在建筑物沉降預測中的應用［J］.測繪工程，2010，19（3）：59－62.