基于BP神經網絡的牛仔織物上漿率預測研究

黃馬壯，田 磊，易長海，2

（1.廣東省均安牛仔服裝研究院，廣東 佛山528329；2.武漢紡織大學，湖北 武漢430200）

牛仔布經紗上漿是牛仔布生產過程的一個重要環節，在生產過程中受到多種工藝因素的影響，其中主要可控因素為漿液濃度、漿槽溫度、漿紗機速度和壓漿輥壓力。在漿紗過程中各工藝參數對上漿率都有不同程度的影響，而不同品種牛仔織物的原紗和織物其上漿率亦不同，因此在確定牛仔漿紗工藝時就應對其上漿率有準確的估測，以保證漿紗的可織性［1］。

本文采用BP神經網絡建立工藝參數與上漿率之間的關系，根據已確定的工藝參數對上漿率進行預測，最后根據上漿率的大小調整工藝參數，從而保證準確控制上漿率。

1 BP神經網絡概言

BP神經網絡，即誤差反向傳播神經網絡，是神經網絡模型中應用最廣泛的一種［2－3］。它由輸入層、隱含層和輸出層構成。假設BP神經網絡每層有N個節點，作用函數為非線性的Sigmoid型函數，一般采用f（x）＝1／（1＋e－x），學習集包括M個樣本模式（Xp，Yp）。對第P個學習樣本（P＝1，2，...，M），節點j的輸入總和記為netpj，輸出記為Opj，則：

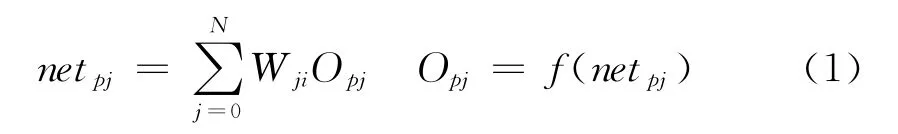
如果任意設置網絡初始權值，那么對每個輸入樣本P，網絡輸出與期望輸出（dpj）間的誤差為：

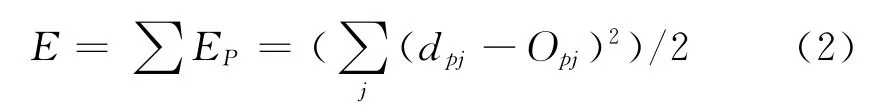
BP網絡的權值修正公式為：

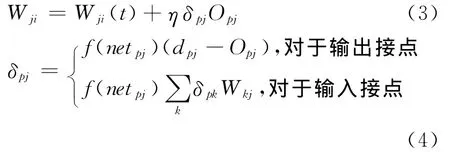
上式中引入學習速率η，是為了加快網絡的收斂速度。通常權值修正公式中還需加一個慣性參數a，從而有：

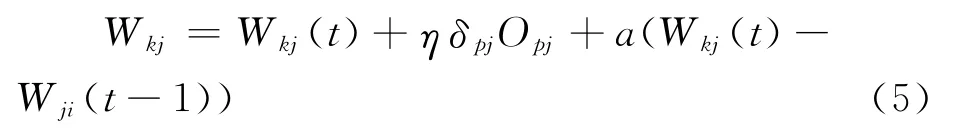
式中，a為一常數項，它決定上一次的權值對本次權值的影響。

2 上漿率預測模型的建立與訓練

2.1 樣本數據的選擇

采用奔達紡織集團漿紗工藝的實際生產數據，其中樣本品種為純棉精梳紗卡，漿紗設備為祖克漿紗機（采用雙漿槽）。根據以上原則，該網絡模型只適用于純棉精梳紗卡這一品種。樣本產品原料相同，織物規格（包括經緯密度、經緯紗線密度、幅寬等）不同，因而上漿率大小有所差別。漿液濃度、漿槽溫度、漿紗機速度和壓漿輥壓力4個因素作為輸入向量，上漿率為輸出向量。具體工藝參數如表1所示。

2.2 建立BP神經網絡模型

第一，首先確立網絡的結構，設置合理的網絡參數（如學習速率），進行網絡權值及閾值初始化。

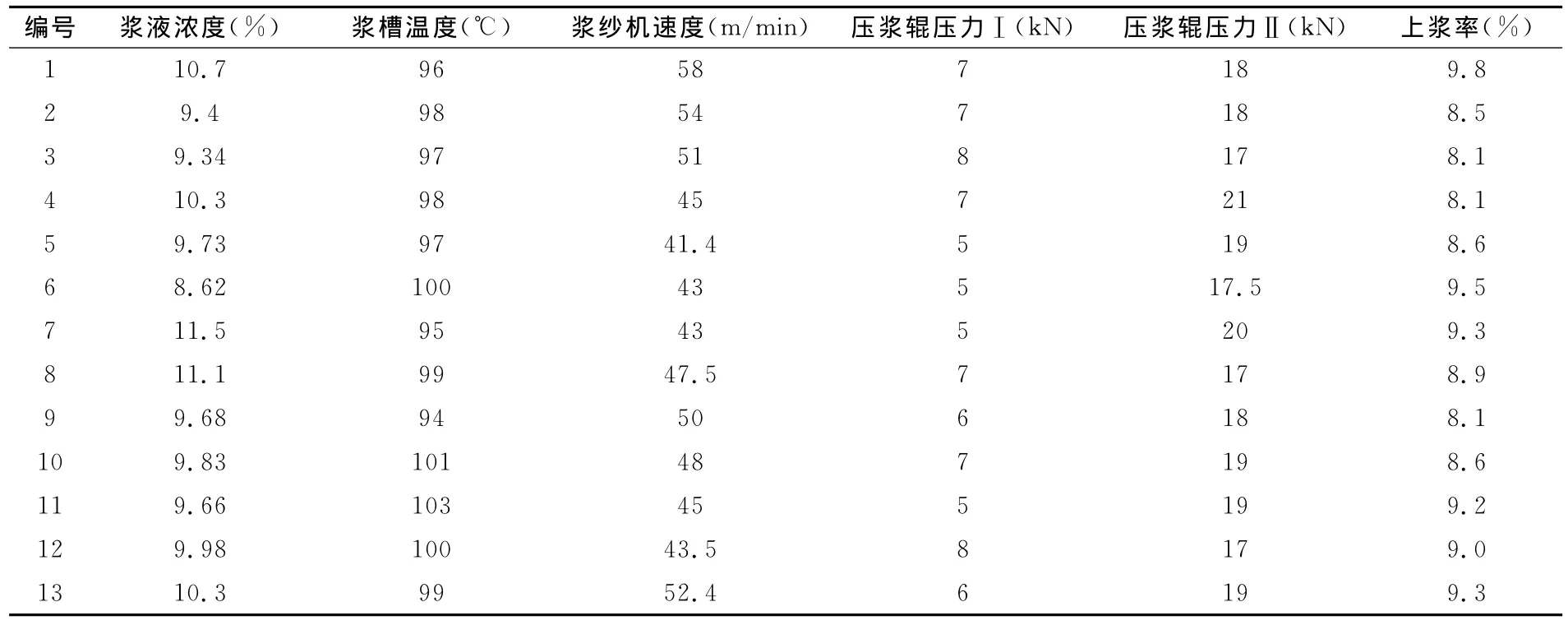
表1 漿紗工藝參數及上漿率

采用3層BP神經網絡：第一層是輸入層，輸入表1中1～10號共10個樣本，每個樣本有5個相關因素，分別是漿液濃度、漿槽溫度、漿紗機速度、壓漿輥壓力（I，II），因此輸入層設定5個神經元；第二層是隱含層，隱層神經元節點數是根據網絡模型訓練時所產生的誤差大小而確定的；第三層是輸出層，由于輸出參數只有上漿率，因此輸出層設1個神經元節點。

第二，確定模型所需的訓練樣本，對每個樣本重復步驟第三～第六。

第三，計算網絡的實際輸出。

每個神經元上作用的函數常用Sigmoid型非線性函數：

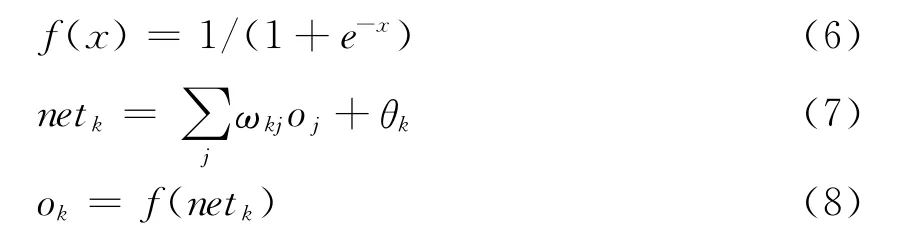
其中，ωkj為從神經元Uk到上一層的神經元Uj的連接權重值；Oj為神經元Uj的輸出，netk為神經元Uk的輸入值；Ok為Uk神經元的輸出；θk為神經元Uk的閾值。由式（7）和式（8）計算神經元Uk的輸入值和輸出值。中間隱層和輸出層的神經元的輸入／輸出也采用這種計算方法。

第四，計算網絡的反向誤差。若樣本容量是k，n是輸出節點個數（在此n＝1），網絡的收斂目標是網絡輸出層的輸出值與實際值的總誤差最小。

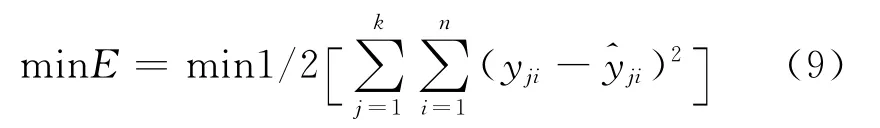
第五，權重學習，修改各層的權重值和闞值。

當誤差不滿足精度要求時，將方差對權重偏導，按梯度下降法修正層間權重值，不斷迭代，致使直到滿足精度E～0為止。權值的調整按下述方法進行，其中，η為學習速率。

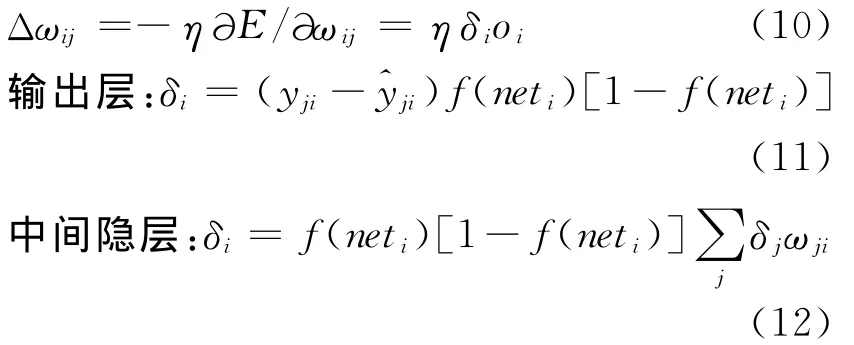
式（12）中，為所有與隱層的神經元相連的輸出層神經元Wli的反傳誤差，于是權值的修正公式為：

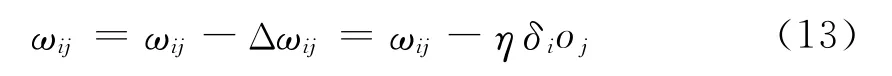
第六，若滿足精度要求，可對上漿率進行預測，否則轉向第二。

這里神經網絡模型采用DPS數據處理系統的BP神經網絡模型實現有指導下的訓練，即以10組數據作為直接訓練數據，2組數據作為訓練檢驗和驗證數據。學習算法采用動量法，學習率采用自適應調整算法。進入BP神經網絡訓練時，可按網絡結構確定網絡參數，這里輸入層設定5個神經元，隱含層l層，隱層神經元節點數為20，Sigmoid參數為0.9，允許誤差0.0001，最大訓練次數2000，并對輸入節點的數值進行標準化轉換。

反復訓練調整網絡參數后確定該模型采用Lvenberg Marquardt算法，訓練函數為trainlm。該網絡的隱含層節點采用logsig作為傳遞函數，輸出層節點采用purelin作為傳遞函數［5］。

圖1為網絡訓練過程的誤差變化曲線圖。實驗發現，模擬復雜程度不高的非線性關系采用這種網絡結構可以達到比較好的效果，在訓練10次后精度已達到10－4，該網絡模型能滿足預設精度，訓練成功。

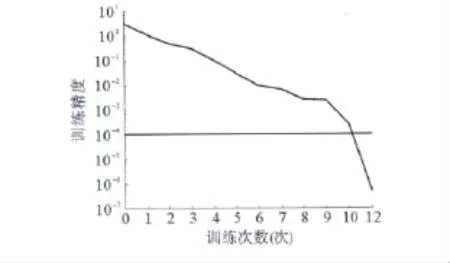
圖1 網絡訓練過程的誤差變化曲線圖

3 網絡模型預測結果與分析

BP網絡運行多次后（這里隱層神經元個數取12），樣本誤差為0.000105。學習訓練樣本組（1＃～10＃）的擬合值與實保實驗值如圖2所示，以及根據BP神經網絡對檢驗和驗證組（11＃～13＃）進行的預測的結果與實際實驗值的比較如圖3所示。

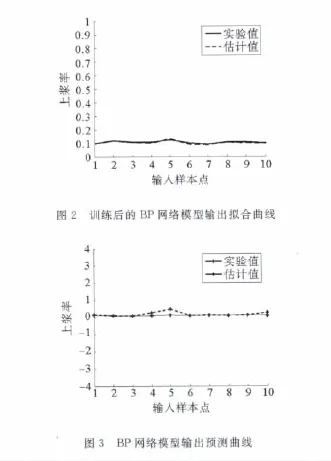
表2 預測上漿率與實際上漿率對比

表2預測結果表明：運用BP神經網絡模型對上漿率進行預測，具有較好的準確性（系統測試相對誤差tmse＝0.0222），不僅對學習樣本的擬合程度高，而且3個檢驗和驗證樣本的預測結果與實驗值非常接近。隨著更多實驗數據的積累和網絡的不斷訓練，會進一步減少網絡訓練時的振蕩，使得預測結果波動范圍不斷減小。

4 結語

4.1 應用BP神經網絡網絡模型對上漿率進行預測，預測上漿率與實際上漿率非常接近，可以滿足實際生產要求。

4.2 BP神經網絡模型能夠比較準確地反映漿紗各工藝參數與上漿率之間的映射關系，運用該模型對上漿率進行預測，誤差在實際生產要求的范圍之內，為漿紗工藝的確定提供了科學依據。

4.3 本模型可以通過擴充樣本數量以及增加樣本種類來提高系統的精度，從而對實際生產起到指導作用。

［1］朱蘇康，陳元甫.織造學［M］.北京：中國紡織出版社，1996.

［2］張立明.人工神經網絡的模型及其應用［M］.上海：復旦大學出版社，1995.

［3］焦李成.神經網絡系統理論［M］.西安：西安電子科技大學出版社，1990.

［4］Kandel E R and Schwarts J.Principles of neural science［M］.Amsterdam：Elsevier，1985.

［5］從爽.面向Matlab工具箱的神經網絡理論與應用［M］.合肥：中國科學技術大學出版社，1998.

［6］劉長勝.基于BP神經網絡的服裝質量預測及其前景［J］.山東紡織科技，2010，（4）：38－41.

［7］張國強.BP神經網絡在紡織服裝上的應用［J］.山東紡織科技，2013，54（2）：37－40.