基于BP神經(jīng)網(wǎng)絡的洪水預測研究

侯 翔，湯元斌 （四川文理學院計算機科學系，四川 達州635000）

洪水預報是一種非常重要的非工程防洪措施，直接影響著防汛、水資源的合理利用和水利工程的管理等。目前，洪水預報模型 （如統(tǒng)計模型、確定性預報模型等）都是以實測數(shù)據(jù)為基礎建立起來的，由于許多條件的限制，上述洪水預報模型難以處理洪水預報中各要素之間的內(nèi)在關(guān)系。為此，筆者基于BP神經(jīng)網(wǎng)絡進行了洪水預測的研究。

1 BP神經(jīng)網(wǎng)絡概述

Rumelhart等［1］為了解決多層前向神經(jīng)網(wǎng)絡的權(quán)系數(shù)優(yōu)化，提出了前饋神經(jīng)網(wǎng)絡的核心算法——BP算法 （Error Back Propagation，BP），通常將使用BP算法的神經(jīng)網(wǎng)絡簡稱為BP神經(jīng)網(wǎng)絡。BP神經(jīng)網(wǎng)絡解決了權(quán)系數(shù)優(yōu)化的問題，被廣泛應用于函數(shù)逼近、模式識別等方面。

BP神經(jīng)網(wǎng)絡通常為3層結(jié)構(gòu)，也可以是多層結(jié)構(gòu)，由輸入層、輸出層和1個隱含層或者多個隱含層組成。BP神經(jīng)網(wǎng)絡的學習步驟如圖1所示，過程分為以下2個階段［2］：①信號正向傳播階段，即輸入信號從輸入層輸入，經(jīng)隱含層，最后進入輸出層被轉(zhuǎn)化成輸出信號。當輸出層不能夠得到理想輸出時，就會轉(zhuǎn)入誤差信號反向傳播。②誤差信號反向傳播階段，即將誤差信號沿輸入信號傳播的途徑，從輸出層開始逐層的向前傳播。在返回過程中，誤差信號不斷調(diào)整各層神經(jīng)元聯(lián)接的權(quán)值。經(jīng)過多次調(diào)整后，使網(wǎng)絡的輸出信號無限逼近于理想輸出。

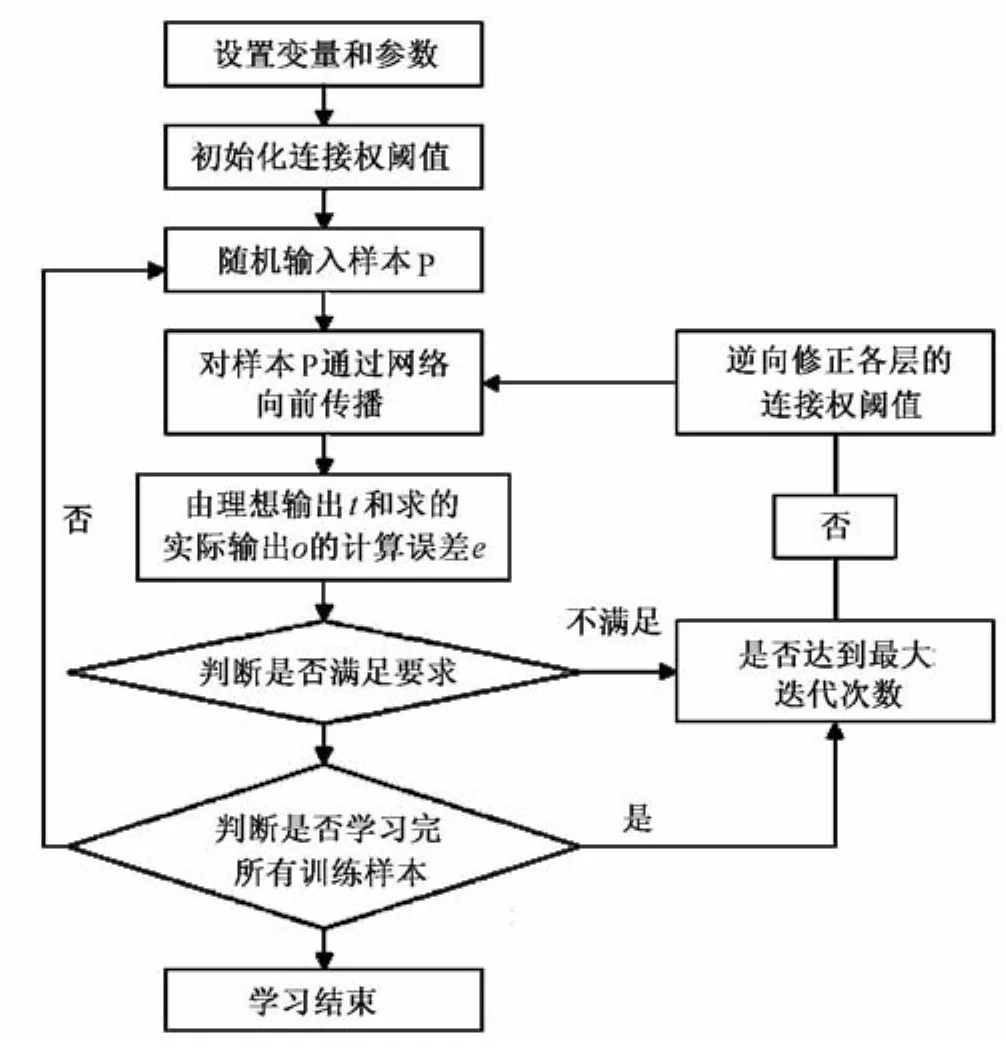
圖1 BP神經(jīng)網(wǎng)絡學習步驟圖

多層BP神經(jīng)網(wǎng)絡模型圖如圖2所示。其中，P為輸入量；f（m）為第m層傳遞函數(shù)；bm為第m層的偏置值；nm為第m層經(jīng)過累加后的凈輸入值；wm為第m層權(quán)值；om為第m層的輸出值。每一層網(wǎng)絡的輸出變成了下一層網(wǎng)絡的輸入，即：

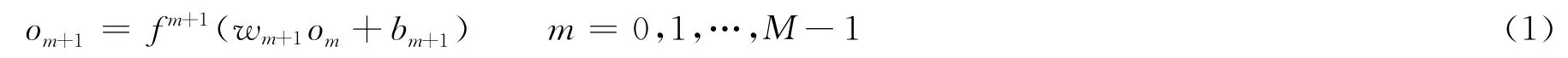
其中首層神經(jīng)元從外部接收的輸入為o0＝p；末層（輸出層）的輸出為：o＝om。

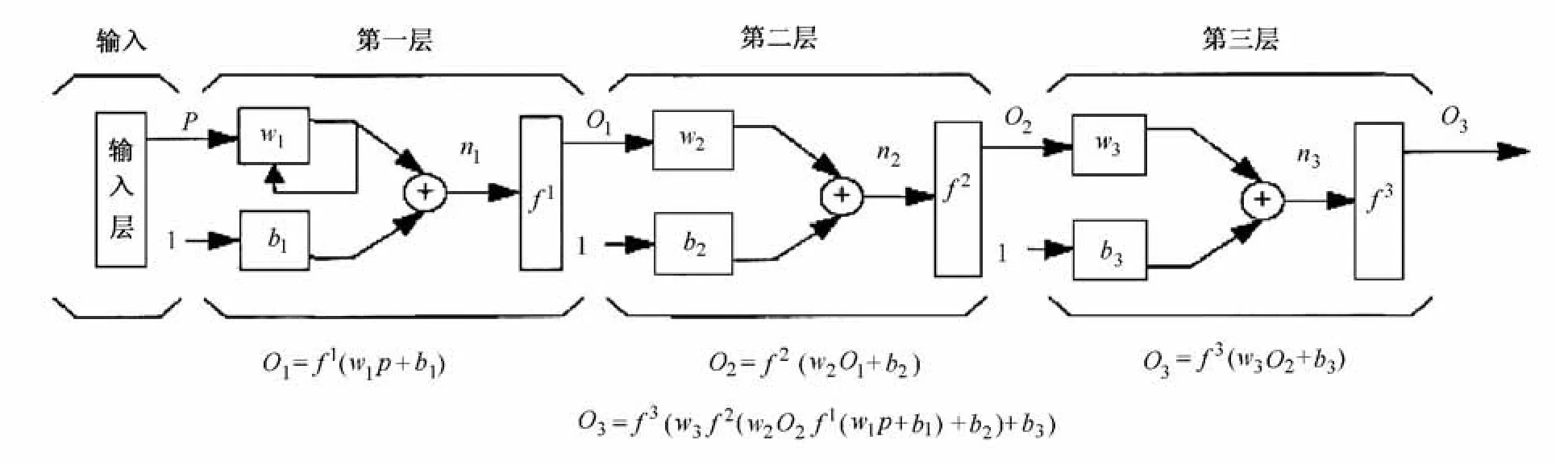
圖2 多層BP神經(jīng)網(wǎng)絡模型圖

LM （Levenberg Marquardt）算法既具有Gauss－Newton法的局部收斂能力，又具備了最速下降法的全局特性［4］。通過自適應調(diào)整阻尼因子來進行收斂，提高了收斂速度，因而訓練速度比其他算法快。LM算法公式如下：

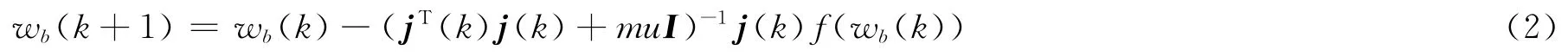
式中，wb為聯(lián)接權(quán)值和閾值的向量；j（k）為一階雅可比矩陣；I為單位矩陣；mu為阻尼因子。

2 洪水預測分析

州河是嘉陵江流域渠江的一條支流，始于宣漢縣江口，蜿蜒流向西南，經(jīng)宣漢城南門、西北、東林、洋烈至千丘旁入達縣境。由東北向西南，經(jīng)達縣羅江鄉(xiāng)紅梁村曹家灣進入達縣境內(nèi)，穿過達州市和達縣的羅江、河市、渡市3個區(qū)的7個鄉(xiāng)，于木頭鄉(xiāng)的大河咀出境，流入渠縣的農(nóng)樂、匯東、匯南等鄉(xiāng)，在三匯鎮(zhèn)與巴河相匯，以下始稱渠江干流。州河流域面積8849km2，河長108km。多年平均流量190m3／s，最大流量13700m3／s （1902年），多年平均徑流總量60.1×108m3。河寬一般為200～300m。

在州河流域范圍內(nèi)，根據(jù)文獻 ［3］對資料的要求，按照易獲取、資料連續(xù)、代表性強等原則［3］，篩選出土黃、毛壩、黃金和東林共計4個水文站作為該流域的代表，采用2001～2006年間4個水文站的部分洪水的流量作為訓練樣本，選擇2007年的流量作為測試樣本。利用相應洪水流量建立BP神經(jīng)網(wǎng)絡模型：

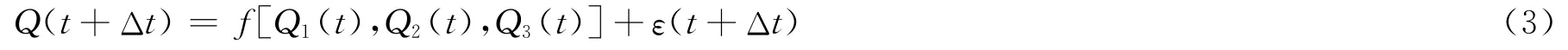
式中，Q、Q1、Q2、Q3分別為東林站、土黃站、毛壩站、黃金站的洪水流量m3／s。

2.1 州河洪水流量預報模型的構(gòu)建

建立州河洪水流量預報模型時，選擇一個輸入層、一個隱含層和一個輸出層的模型結(jié)構(gòu)。輸入層為3個節(jié)點，即土黃站、毛壩站、黃金站的洪水流量 Q1（t）、Q2（t）、Q3（t）；中間層為隱含層，需要通過實驗來確定隱層的結(jié)點數(shù)；輸出層為一個節(jié)點，即東林站洪水流量Q（t＋Δt），模型結(jié)構(gòu)如圖3所示。

BP神經(jīng)網(wǎng)絡的傳遞函數(shù)分為線性和非線性2種類型。由于研究對象為洪水，其具有非線性關(guān)系的特征，因而在建立BP神經(jīng)網(wǎng)絡時，傳遞函數(shù)采用Sigmoid函數(shù)。為了加快BP神經(jīng)網(wǎng)絡的收斂性，有必要對所有的輸入值加以歸一化［4］：

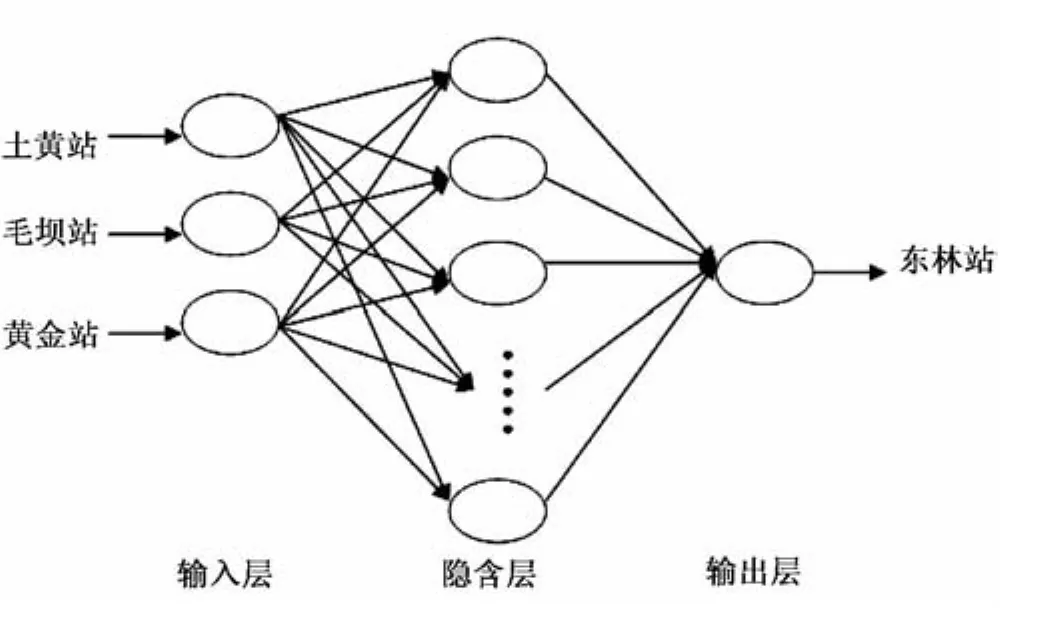
圖3 州河洪水流量預報模型結(jié)構(gòu)圖

式中，p為當前學習樣本；pmax為學習樣本中的最大值；pmin為學習樣本中的最小值；y為訓練歸一化后的數(shù)據(jù)。

2.2 模型的檢驗

要選擇出符合實際情況的BP神經(jīng)網(wǎng)絡模型，其中最關(guān)鍵的一步是利用預測樣本來不斷測試已經(jīng)訓練好的模型，直到選出適合的模型。而判斷一個BP神經(jīng)網(wǎng)絡是否符合實際情況，主要觀察其預測能力的高低，為此必須利用測試數(shù)據(jù)對已訓練好的模型進行檢驗。優(yōu)選網(wǎng)絡訓練參數(shù)為：預測精度goal＝0.0001，學習速率lr＝0.001，訓練次數(shù)epochs＝20000，網(wǎng)絡所用訓練函數(shù)為trainlm，其余參數(shù)取默認值。將已訓練好的 （穩(wěn)定性與收斂性都符合要求）BP神經(jīng)網(wǎng)絡模型對2007年汛期 （5～10月）中33次洪水流量進行預報，并以文獻 ［3］的規(guī)定為標準，對預報模型效果進行評定。

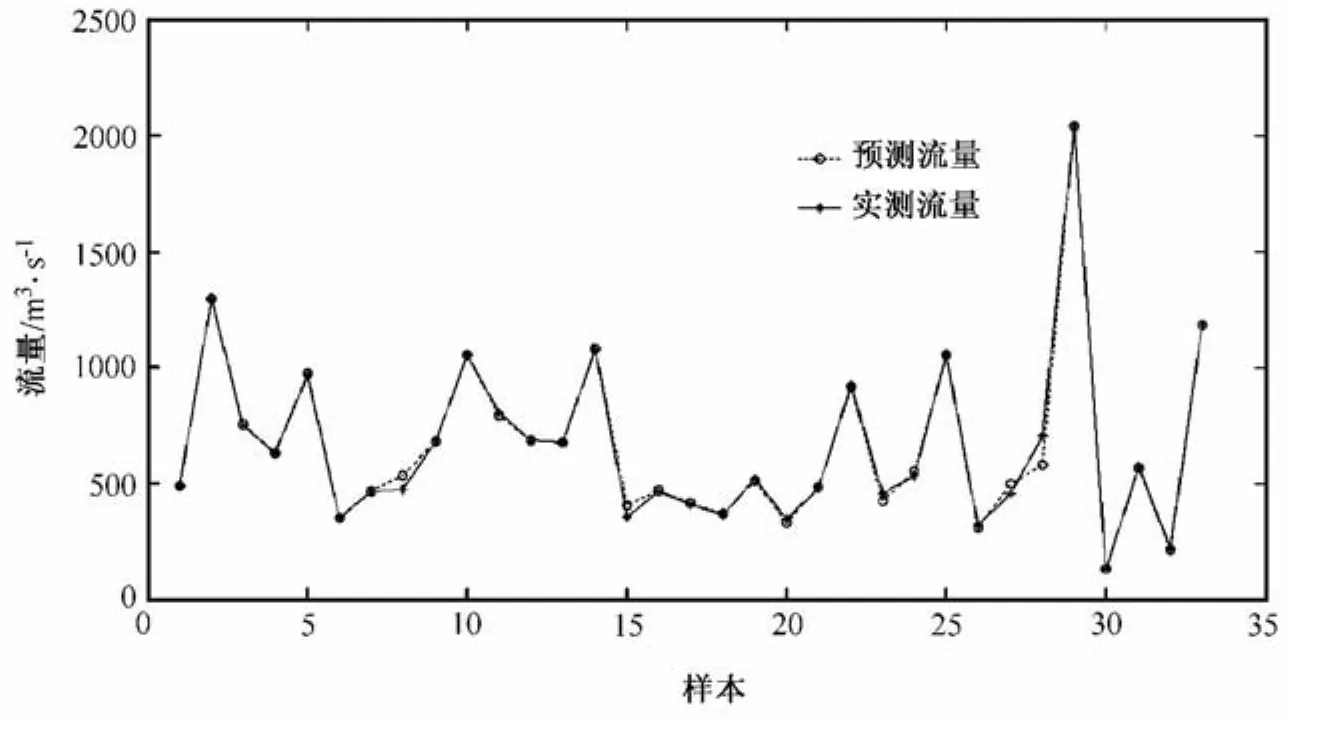
圖4 基于BP神經(jīng)網(wǎng)絡模型的洪水預報流量與實測流量對比圖

基于BP神經(jīng)網(wǎng)絡模型的洪水預報流量與實測流量對比圖如圖4所示。由圖4可知，基于BP神經(jīng)網(wǎng)絡模型的洪水預報流量與實測流量十分吻合，說明采用LM算法的預報精度高，能夠應用于洪水預報。

3 結(jié) 語

洪水具有不確定性即非線性的特點，而人工神經(jīng)網(wǎng)絡能夠處理大規(guī)模復雜非線性動力學問題。探討了利用BP神經(jīng)網(wǎng)絡進行洪水預報的可行性。以州河上游段土黃站、東林站及區(qū)間支流的洪水為研究對象，基于BP神經(jīng)網(wǎng)絡建立考慮區(qū)間支流的洪水預測模型，利用該模型對東林站2007年的洪水進行了預測，預測結(jié)果與實測值十分符合，說明基于BP神經(jīng)網(wǎng)絡的洪水預測模型具有可行性。

［1］閔祥宇 .基于人工神經(jīng)網(wǎng)絡的渭河上游洪水預報研究 ［D］.蘭州：蘭州大學，2011.

［2］范睿 .基于遺傳算法的神經(jīng)網(wǎng)絡洪水預報研究與應用 ［D］.哈爾濱：哈爾濱工程大學，2005.

［3］SL250－2000，水文情報預報規(guī)范 ［S］.

［4］閻平凡，張長水 .人工神經(jīng)網(wǎng)絡與模擬進化計算 ［M］.北京：清華大學出版社，2000：26－27.