基于經驗風險的中心文本分類算法
周曉堂,歐陽繼紅,李熙銘
(吉林大學 計算機科學與技術學院,長春 130012)
互聯網的快速發展為信息共享提供了一個通用平臺.文本是信息的主要載體,研究文本自動分類可系統地規范文本,提高信息檢索速度,因此,對文本分類算法的研究具有重要意義[1].近年來,人們已提出了許多文本分類算法,包括中心分類法[2]、樸素Bayes算法[3]、支持向量機[4]、人工神經網絡[5]、K近鄰算法[4]和決策樹[6]等.其中,中心分類法具有高效、健壯和計算簡便并易于編程等優點,得到廣泛應用.但中心分類法的訓練過程忽略了文本權值對類別中心的影響.針對中心分類法的缺陷,目前已提出了許多改進.文獻[7]提出的權重調整方法中,使用特征的“純度”表示每個特征的區別能力,然后根據驗證集上的錯誤率使用“純度”迭代調整文本向量中的所有特征權重,該方法認為平均分配在各類中的特征具有較低的“純度”和區別能力,而非平均分布在各類中的特征具有較高的“純度”和區別能力.文獻[8]提出的基于特征分布方法中,考慮了特征在類中的分布,并使用特征分布加強特征權重函數.文獻[9]提出的類-特征-中心方法中,應用類間和類內特征索引構建相對于傳統方法具有更好初始值的類中心向量.文獻[10]提出的拖拽方法利用訓練集上的分類錯誤信息通過拖拽方法改善類中心向量,并提出了按組更新的中心分類法,該方法對類中心進行拖拽,使其靠近屬于該類且被錯誤分到其他類的文本,同時遠離不屬于該類且被錯誤分到該類的文本.在引入訓練集分類錯誤信息的基礎上,為提高模型分類的泛化能力,譚松波等[11]又引入了訓練集邊界信息,定義了數據的假設邊界,并依此對類中心進行拖拽,使類中心靠近屬于該類且處在假設邊界附近的文本,該方法利用訓練集上的分類錯誤信息和訓練集的邊界信息定義了目標函數,通過利用梯度下降法求得目標函數的最小值指導類中心的拖拽.但該方法給出的目標函數并不處處光滑、可導,在應用梯度下降方法時,可能會產生異常結果.
本文在傳統中心分類法的基礎上,基于經驗風險最小化原則構建目標函數,通過引入Sigmoid函數平滑得到一個處處光滑、可導的目標函數,解決了文獻[11]中目標函數的可導性問題.使用最優化技術優化目標函數調整類中心向量,求得了代表性更強的類中心向量,進而提高了分類性能.實驗結果表明,本文算法具有與支持向量機相近的分類性能,并適用于偏斜數據集,魯棒性較強.
1 中心分類法
中心分類法的基本思想:根據訓練文本集合的信息為每個類別構建中心特征向量作為該類的代表向量,待分類文本則根據與各個中心特征向量的相似度決定所屬類別.
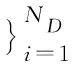
1) 預處理階段.使用向量空間模型處理非結構化的文本數據,計算每個文本對應的數值特征向量d=(w(t1,d),w(t2,d),…,w(tNT,d)),各項特征權重w(ti,d)的計算公式為
(1)
該數值特征向量由特征空間中的特征權重組成,包含了文本內部潛在的統計信息.其中:d表示來自訓練集的一篇文本;tf(ti,d)表示在文本d中特征ti的出現次數;Nti表示訓練集D中包含特征ti的文本總數;分母為規范化因子,使每個數值特征向量都具有單位長度,消除不同文本的不同長度對特征權重的影響.
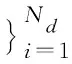
(2)
3) 測試階段.中心分類法使用余弦函數度量測試文本d和類別中心Ci的相似度.相似度計算公式為
(3)
其中,“·”表示兩個向量的點積.
經過相似度對比,中心分類法認為測試文本d屬于與文本d具有最大相似度類別中心所代表的類別.引入變量Cjudge(d,C),判別公式為
(4)
2 本文算法
傳統中心分類法使用算術平均值計算類別的中心向量.該策略給每篇文本相同的權重,未考慮不同文本的表達能力是不同的,影響了中心向量的表達能力,從而影響了中心分類法的分類性能.針對此問題,本文基于經驗風險最小化的原則構建目標函數,通過梯度下降算法計算目標函數極值點求得類別中心向量.同時,為了解決文獻[11]中目標函數不是處處可導的問題,本文引入Sigmoid函數平滑目標函數,避免其不可導產生的不穩定因素.
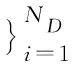
(5)
其中: 函數Cneighbor(d,C)表示集合C中與文本d的相似度最高且屬于不同類別的類中心向量;函數Ctrue(d,C)表示集合C中與文本d同類的類中心向量;函數Sgn(x)是指示函數,定義如下:
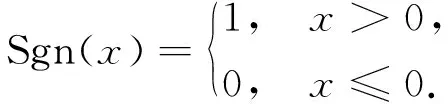
(6)
由式(6)可見,當函數Sgn(cos(d,Cneighbor(d,C))-cos(d,Ctrue(d,C)))=0時,表明文本d被正確分類;否則,表明文本d被錯誤分類.因此,目標函數RSgn(D,C)有效表達了中心分類法在訓練集D上的經驗誤差.
通過最小化函數RSgn(D,C),可得到更具代表性的類中心,提高中心分類法的分類性能.但由于指示函數Sgn(x)的階梯函數性質,使得目標函數RSgn(D,C)不是處處光滑且不可導,不能直接使用解析法求解極值.因此,本文使用平滑單調函數Sigmoid(x)近似模擬指示函數Sgn(x),以得到處處光滑、可導的目標函數RSig(D,C),定義如下:
(7)
其中
(8)
λ為控制Sigmoid(x)函數形狀的參數.
最后,得到類中心的梯度更新公式為
(9)
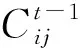
(10)
其中
(11)
在經驗風險最小化原則下,使用梯度下降法獲得最優類中心的算法偽代碼如下:
輸入:訓練集D,最大迭代次數Max_iter.
輸出:最優類中心向量集CMax_iter.
按式(2)初始化起始類中心向量集C0
Fort=1∶Max_iter//迭代開始;
Fori=1∶ND//迭代的第一部分
計算文本di和當前所有類中心Ct-1的相似度
計算文本di的Cneigbor(di,Ct-1)值
End for
Fori=1∶K//迭代的第二部分
Forj=1∶NT
按式(9)更新類中心
End for
End for
End for//迭代結束
ReturnCMax_iter
3 實驗結果
3.1 實驗數據集及評價標準
實驗數據集選取來自TREC,OHSUMED和Reuters-21578這3個基準文本數據集中的4個子文本數據集la12,new3,ohscal和re1.其中: la12和new3來自TREC;ohscal來自OHSUMED;re1來自Reuters-21578.4個子文本數據集la12,new3,ohscal和re1的特征列于表1.由數據集規模大小可見,la12和ohscal是大數據集,new3和re1是小數據集;由數據集平衡程度可見,la12,ohscal,new3是平衡數據集,re1是不平衡數據集.
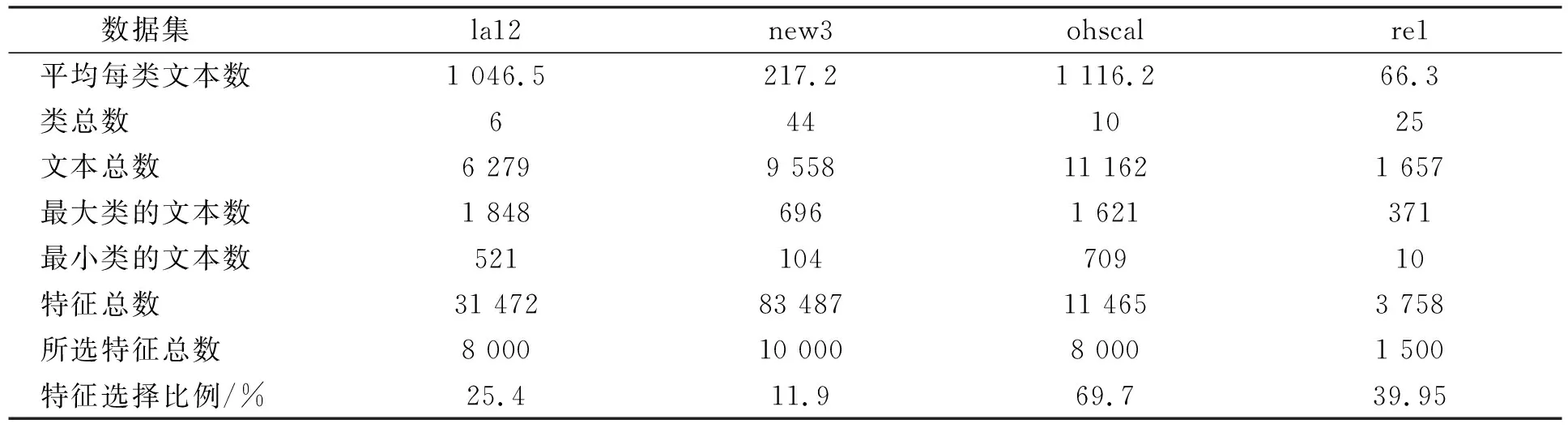
表1 文本數據集Table 1 Text data
實驗選用宏平均F1值和微平均F1值[12]度量分類性能.宏平均F1值為整個測試集上的F1值,微平均F1值為測試集各類別上F1值的均值.F1值為查準率和查全率的調和平均值,定義如下:
F1=2×[(查準率×查全率)/(查準率+查全率)].
(12)
3.2 實驗結果
為了獲得模型預測能力的準確估計,減弱訓練集、測試集分割時對實驗結果產生的影響,實驗過程采用三折交叉驗證方式[13].實驗選取的對比算法包括傳統中心分類法(BCC)及支持向量機的兩個變體SVMTorch和LibSVM.實驗結果如圖1和圖2所示.
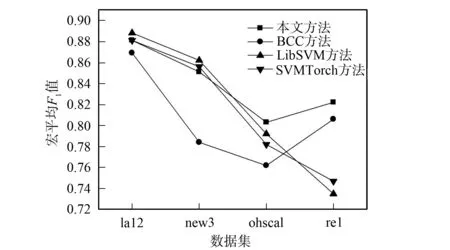
圖1 不同方法的宏平均F1值對比Fig.1 Comparison of macro-F1 mean values by different methods

圖2 不同方法的微平均F1值對比Fig.2 Comparison of micro-F1 mean values by different methods
由圖1和圖2可見,本文算法的分類性能明顯高于傳統中心分類法.此外,本文算法在彌補了傳統中心分類法在平衡數據集上分類性能較差的缺點、使其分類性能逼近支持向量機方法的同時,進一步增強了傳統中心分類法在偏斜數據上分類性能較強的優勢,使其分類性能明顯優于支持向量機方法.
綜上所述,本文提出的經驗風險最小化原則下的中心分類法相比于傳統中心分類法,能得到代表性更強的類中心,其分類性能逼近支持向量機方法,且在偏斜數據集上優于支持向量機方法.
[1] XUE Gui-rong,XING Di-kan,YANG Qiang,et al.Deep Classification in Large-Scale Text Hierarchies [C]//Proceedings of the 31st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval.New York: ACM,2008: 619-626.
[2] Han E H,George K.Centroid-Based Document Classification: Analysis and Experimental Results [C]//Proceedings of the 4th European Conference on Principles of Data Mining and Knowledge Discovery.London: Springer-Verlag,2000: 424-431.
[3] Ashraf M K,Eibe F,Bernhard P,et al.Multinomial Naive Bayes for Text Categorization Revisited [C]//Proceedings of the 17th Australian Joint Conference on Artificial Intelligence.Berlin: Springer Verlag,2004: 488-499.
[4] Naohiro I,Tsuyoshi M,Takahiro Y,et al.Text Classification by Combining Grouping,LSA and kNN [C]//Proceedings of the 5th IEEE/ACIS International Conference on Computer and Information Science.Washington DC: IEEE Computer Society,2006: 148-154.
[5] Rowena C,Chunghsing Y,Katea S.A Neural Network Model for Hierarchical Multilingual Text Categorization [C]//Proceedings of the Second International Symposium on Neural Networks.Berlin: Springer Verlag,2005: 238-245.
[6] GAO Sheng,WU Wen,LEE Chin-hui,et al.A Maximal Figure-of-Merit (MFoM)-Learning Approach to Robust Classifier Design for Text Categorization [J].ACM Transactions on Information Systems,2006,24(2): 190-218.
[7] Shrikanth S,George K.A Feature Weight Adjustment Algorithm for Document Categorization [C]//Proceedings of the KDD-2000 Workshop on Text Mining.Boston: Citeseer,2000: 12-19.
[8] Verayuth L,Thanaruk T.Effect of Term Distributions on Centroid-Based Text Categorization [J].Information Sciences,2004,158: 89-115.
[9] GUAN Hu,ZHOU Jing-yu,GUO Min-yi.A Class-Feature-Centroid Classifier for Text Categorization [C]//Proceedings of the 18th International Conference on World Wide Web.New York: ACM,2009: 201-210.
[10] TAN Song-bo.Large Margin DragPushing Strategy for Centroid Text Categorization [J].Expert Systems with Applications,2007,33(1): 215-220.
[11] TAN Song-bo,CHENG Xue-qi.Using Hypothesis Margin to Boost Centroid Text Classifier [C]//Proceedings of the 2007 ACM Symposium on Applied Computing.New York: ACM,2007: 398-403.
[12] Michael B,Fredric G.The Relationship between Recall and Precision [J].Journal of the American Society for Information Science,1994,45(1): 12-19.
[13] Christopherd M,Prabhakar R,Schütze H.Introduction to Information Retrieval [M].New York: Cambridge University Press,2008: 151-176.

