連續剛構橋頂推力計算與優化分析

李 杰，陳 彬

(1.鄭州大學土木工程學院，河南鄭州450001;2.河南高速監理咨詢有限公司，河南鄭州450000)

0 引言

連續剛構橋采用懸臂施工，施工現場的合龍溫度以及成橋后混凝土收縮、徐變效應對連續剛構橋主梁和橋墩的變形具有較大影響，此外運營過程中，由于混凝土收縮、徐變的影響，主梁跨中產生下撓變形引起主墩向跨中方向的偏位.為了消除該不良影響，實際施工中通過施加合龍頂推力使主墩產生反向預偏量，以達到抵消后期混凝土收縮徐變產生的主墩水平位移的目的［1-2］.

連續剛構橋合龍頂推力計算已有的研究多采用解析法，如文獻［3］采用消除墩頂水平位移法和消除主梁拉力法分別計算了合龍頂推力;文獻［4］推導了連續剛構橋中跨合龍時合龍頂推力的解析公式;文獻［5］提出在一般情況下選擇低溫合龍對結構受力是有利，給出了連續剛構橋在高溫合龍情況下采取預施加反頂力的施工對策.此外還有一些文獻對連續剛構橋合龍力計算、高溫合龍措施進行了討論［6］.筆者以三淅高速白水峪大橋為例，通過分析不同組合的次中跨和中跨頂推力對成橋線形影響，確定合龍頂推力的取值，分析合龍溫度對成橋線形的影響，并根據實際合龍溫度對頂推力進行修正.

1 工程概況及有限元建模

1.1 工程概況

白水峪大橋，是三門峽至淅川高速公路靈寶至盧氏段上的一座五跨預應力混凝土連續剛構橋.大橋分為左右兩幅，左幅橋位于R=2 500 m的左偏圓曲線內，右幅橋位于R=2 900 m的右偏圓曲線內.大橋跨徑組成為65 m+3×120 m+65 m，主梁截面采用單箱單室，頂板寬12.5 m，底板寬7 m，頂板懸臂長度2.75 m;箱梁根部梁高7.3 m，跨中梁高2.7 m.主橋橋墩采用雙肢等截面矩形實體薄壁墩，雙肢間距5.6 m，單肢截面尺寸7×1.7 m，最大的墩高為77 m;大橋采用掛籃懸臂澆筑施工.左幅橋立面布置如圖1所示.

1.2 有限元建模及成橋后變形

采用橋梁結構分析軟件MIDAS/Civil進行數值仿真分析，全橋采用空間梁單元模擬.主梁和橋墩的連接采用主從節點剛性連接模擬.施工過程中的施工荷載如節段濕重、掛籃重量，采用節點力和節點彎矩模擬，同時模型中考慮混凝土收縮徐變效應、水泥強度隨時間增長效應.主梁控制截面編號如圖1所示，其中截面A、F為邊跨支承處截面，截面 B、C、D、E 為墩頂截面.

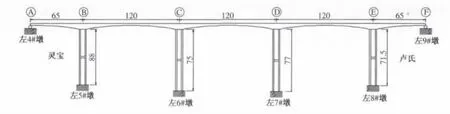
圖1 白水峪大橋立面布置(單位:m)Fig.1 Elevation view of Baishuiyu Bridge(unit:m)

成橋運營階段導致墩頂水平位移的主要原因是長期荷載作用下混凝土收縮、徐變及實際合龍溫度與設計合龍溫度的合龍溫差等因素.在設計的合龍方案下，通過有限元軟件模擬整個施工過程，并計入1 000 d(約3 a)的混凝土收縮徐變，得出成橋1 000 d后主梁的水平位移，其中4#、5#、8#和9#墩頂發生較大的水平位移.主梁水平位移的正方向為曲線的切線方向，以橋梁大里程方向為正.當不施加頂推力時，成橋1 000 d后各個控制截面處的位移如表1所示.

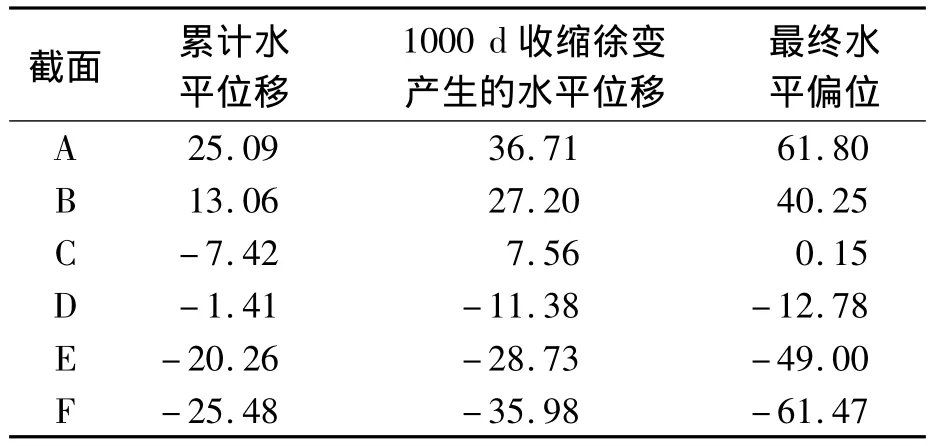
表1 主梁的水平位移(未施加頂推力)Tab.1 The horizontal displacement of main beam(not apply jacking force) mm

從表1可以看出，當合龍時未施加頂推力對于成橋運營階段主梁的變形是不利的，因此施加合龍頂推力很有必要.

2 頂推力計算方法

根據實際施工的合龍方案，先合龍次中跨，后合龍中跨.在次中跨頂推力作用下，5#、8#墩的水平位移為有利的水平位移，6#、7#墩的水平位移為不利的水平位移.在中跨頂推力作用下，增大5#、8#墩的有利水平位移，減小了6#和7#的不利水平位移.因此，中跨頂推力不應小于次中跨頂推力，首先取中跨頂推力為次中跨頂推力2倍進行研究.次中跨頂推力記為f，那么中跨頂推力為2f，頂推力施加如圖2所示.

將次中跨頂推力f分別取值為0，100，200 kN，此時對應的中跨頂推力為0，200，400 kN，通過計算得出各墩頂控制截面水平位移如表2所示.

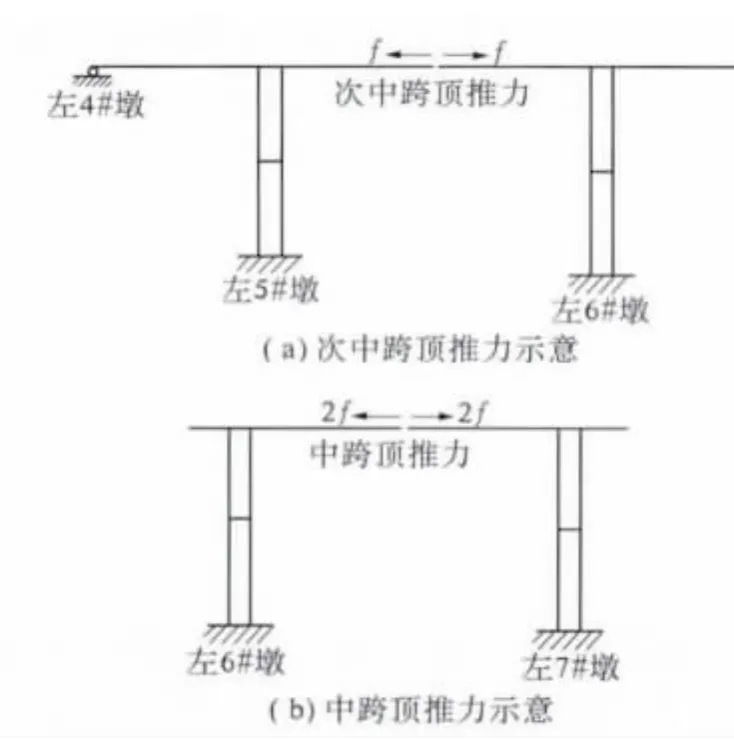
圖2 頂推力施加示意Fig.2 Diagram of jacking force

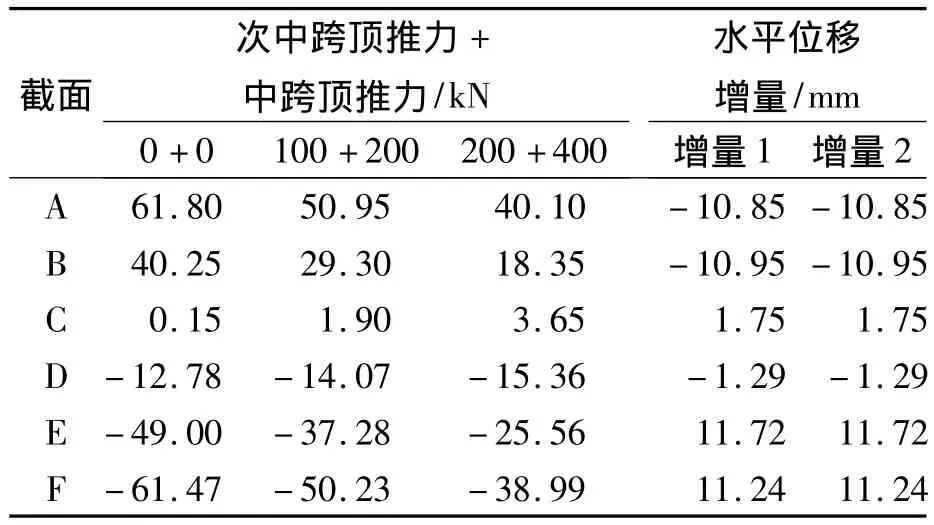
表2 不同的次中跨、中跨頂推力作用下控制截面水平位移Tab.2 The section displacement under different jacking force of sidem id-span and m id-span

表2中增量1為頂推力組合(100+200)kN與組合(0+0)下控制截面的水平位移差值，增量2為組合(200+400)kN與組合(100+200)kN下控制截面的差值，其余表格中增量的含義類同.從表2的數據可以看出，當次中跨和中跨頂推力成倍增加時，各控制截面的水平位移的相鄰組合增量相同.為了研究主梁水平位移受次中跨頂推力和中跨頂推力的影響程度，取次中跨頂推力為100 kN，中跨頂推力依次取為為200，300，400 kN.計算各墩頂控制截面處水平位移如表3所示.從表3可以得出，次中跨頂推力不變時，各控制截面處的水平位移隨著中跨頂推力的增大呈線性變化.綜合表2和表3的水平位移變化規律，計算出次中跨頂推力為 400，450，500，550 kN，中跨頂推力為1 200 kN時主梁各控制截面處水平位移，計算結果如表4所示.

從表4可以看出，當中跨頂推力不變時，各控制截面處的水平位移隨著次中跨頂推力的增大呈線性變化.根據表3和表4的可以得出，中跨頂推力和次中跨頂推力對主梁水平位移的影響程度.當頂推力增大100 kN時各控制截面的水平位移如表5所示.從表5可以看出，當次中跨頂推力增加時對A、B、E、F截面水平位移有利，但是對C、D截面水平位移不利;當中跨頂推力增大時對所有截面來說均有利，對A、B、E、F截面水平位移的影響程度是次中跨頂推力影響程度的54%左右.因此，在頂推力的優化中應著重調整次中跨頂推力的大小.根據上述規律得出多種頂推力組合下主梁各控制截面的水平位移值如表6所示.

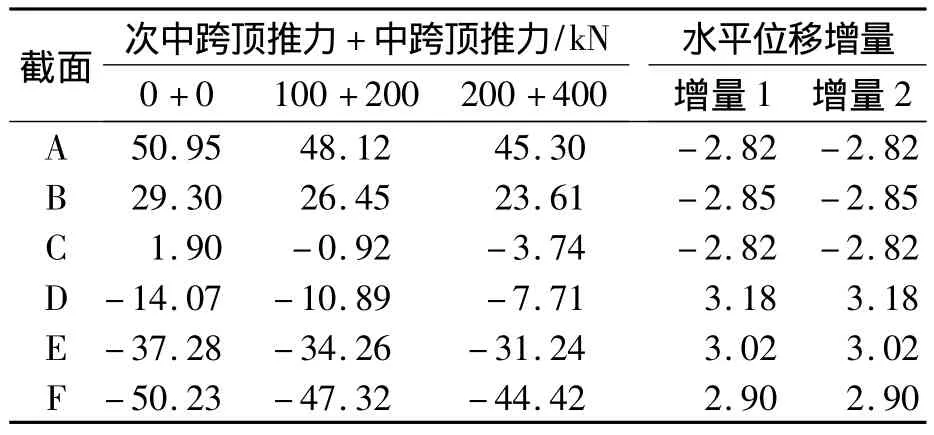
表3 不同的中跨頂推力作用下控制截面水平位移Tab.3 The section disp lacement under different jacking force ofm id-span mm

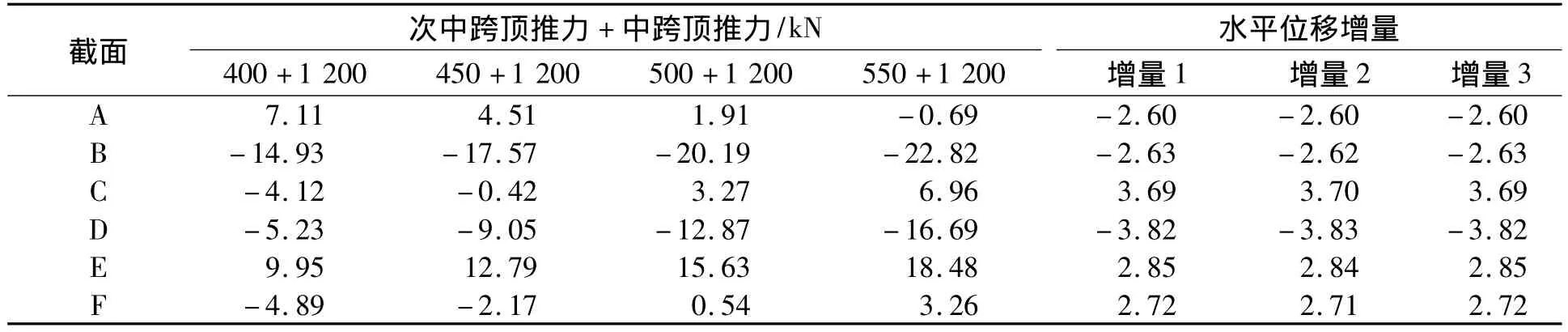
表4 不同的次中跨頂推力作用下控制截面水平位移Tab.4 The section displacement under different jacking force of sidem id-span mm

從表6可以看出，當次中跨頂推力為500 kN、中跨頂推力為1 300 kN時，基本可以抵消成橋1 000 d后主梁上各控制截面的不利水平位移，相比設計圖紙給定的頂推力組合(次中跨頂推力700 kN、中跨頂推力1 500 kN)來說，在一定程度上實現了對頂推力的優化.

3 溫度對合龍的影響

當實際合龍溫度低于設計合龍溫度時，即在低溫狀態下合龍，成橋后的合龍溫差會產生有利的升溫效應［7-9］.同理，當實際合龍溫度高于設計合龍溫度時，成橋后因降溫將導致墩頂產生由邊跨往中跨方向的水平位移，主梁及橋墩將產生溫度附加內力，當溫度附加內力超出設計容許的范圍，將影響結構安全.為了消除合龍溫差的不利影響，可在合龍時通過頂推力進行調整.當整體升溫0，2，4，6，8，10 ℃時主梁主要控制截面的水平位移如表7所示.

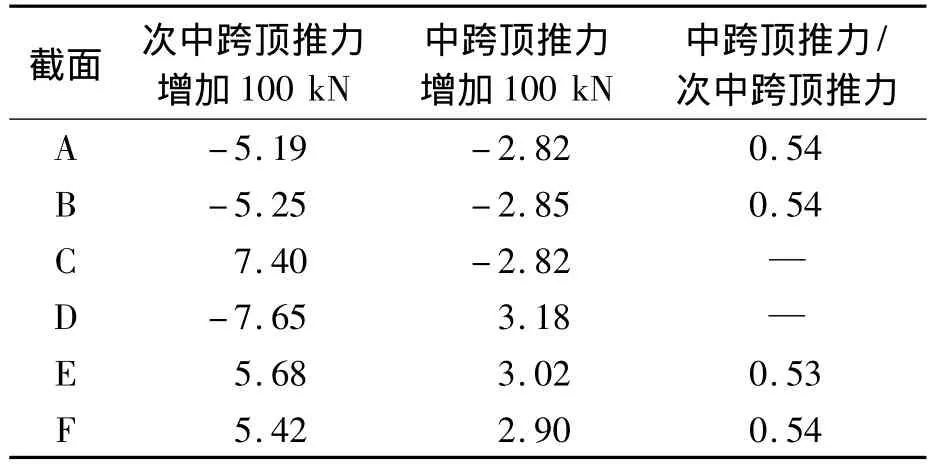
表5 次中跨和中跨頂推力分別增大100 kN下主梁水平位移Tab.5 The displacement of beam under the increase 100 kN of side-m iddle and m id-span’s jacking force mm

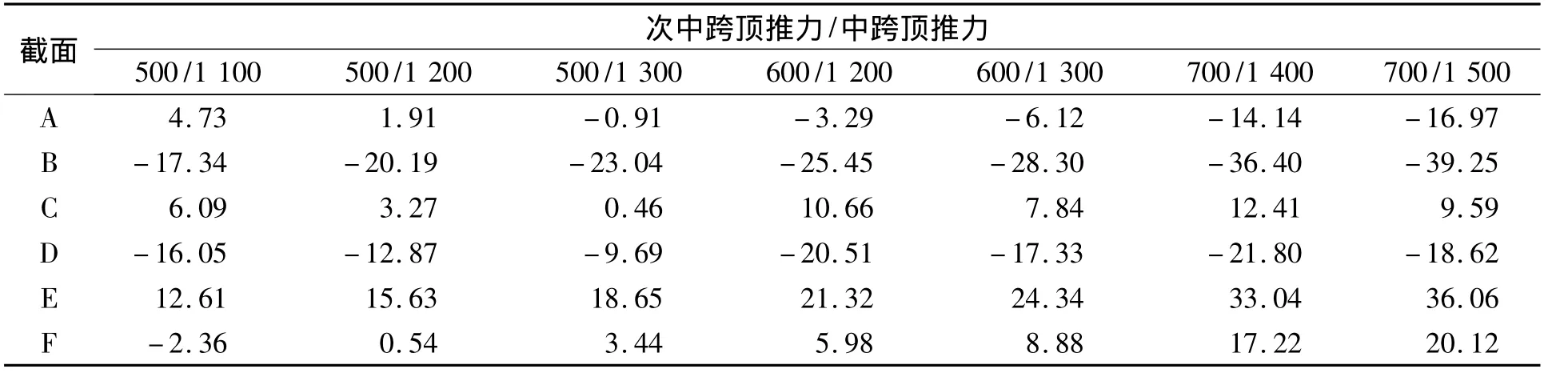
表6 不同的頂推力下主梁控制截面水平位移Tab.6 The disp lacement of beam’s control section under the different jacking force mm

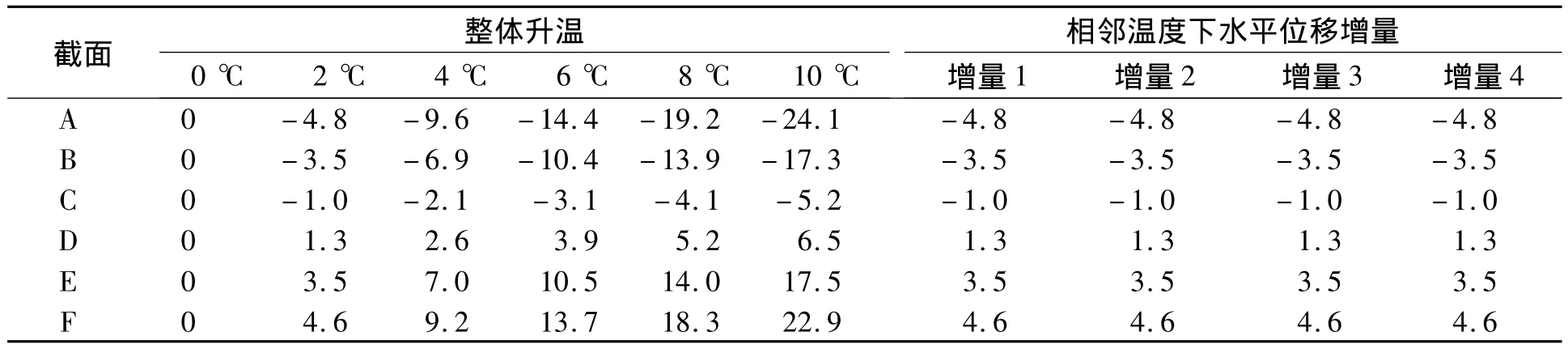
表7 溫度變化作用下主梁控制截面水平位移Tab.7 The displacement of beam’s control section under the effect of tem perature change mm

表7中增量1為整體升溫2℃與0℃下主梁控制截面的水平位移增量，增量2為整體升溫4℃與2℃下主梁控制截面的水平位移增量，其余依次類推.從表7可以看出，相鄰溫度下主梁控制截面的水平位移增量相等，說明升溫時主梁主要控制截面的水平位移隨著溫度的升高呈線性增大，同理降溫時主梁各控制截面的水平位移也呈線性減小.從表7還可以看出，溫度變化對截面A處的水平位移影響較大.通過計算合龍溫差對截面A水平位移的大小來優化次中跨頂推力，則可得到合龍溫差產生的合龍變形需優化的頂推力公式如式(1)所示:

式中:Δf為因溫差需要調整的頂推力，kN;Δt為設計溫度和實際現場溫度的差值，℃;δtA為溫度每降低1℃引起截面A處的水平位移，mm;δfA為次中跨頂推力每增加1 kN引起截面A處的水平位移，mm.

白水峪大橋設計圖紙給出的合龍溫度為12～22℃，大橋在初冬合龍，現場合龍的溫度會低于該合龍溫度區間，根據本文的方法對次中跨頂推力進行調整.當合龍時溫度為6℃時，次中跨頂推力需要減小Δf，Δt=6℃，由表5可得δfA=0.051 9 mm，由表7可得δtA=2.4 mm.所以 Δf=6×2.4/0.051 9=277.45 kN.

4 結論

(1)采用有限元數值方法對多跨連續剛構橋合龍頂推力進行分析直觀簡捷，同時可以根據施工中合龍溫度的不同，應用參數間簡單的公式及時優化和修正頂推力大小.

(2)對于五跨連續剛構橋來說，次中跨頂推力和中跨頂推力對各墩頂水平位移的影響程度不同，增大次中跨頂推力對于邊跨主墩的水平位移有利，而對于中跨主墩的水平位移不利;增大中跨頂推力對于所有主墩的水平位移均有利;在五跨連續剛構橋頂推力調整中著重調整中跨頂推力.

(3)主梁各控制截面處的水平位移隨著合龍溫度的升高呈線性增大，同理隨著合龍溫度的降低呈線性減小.當實際合龍溫度和設計合龍溫度存在差值時，可以通過改變頂推力的大小改善合龍溫差對結構產生的影響.

［1］ 徐建國，陳淮，王博，等.連續箱梁橋力學性能分析［J］. 鄭州大學學報:工學版，2004，25(1):28-30.

［2］ 張剛剛，吳重男.連續剛構橋合龍段頂推力設計探討［J］. 中外公路，2011，35(5):119-122.

［3］ 殷燦彬，王解軍，唐燦.連續剛構橋高溫合龍頂推力的計算方法研究［J］.中南林業大學學報，2009，29(1):111-116.

［4］ 鄒毅松，單榮相.連續剛構橋合龍頂推力的確定［J］. 重慶交通學院學報，2006，25(2):12-15.

［5］ 周光偉，陳得良，劉榕.連續剛構橋合龍溫度的合理確定及高溫合龍對策［J］.重慶交通學院學報，2006，22(3):15-19.

［6］ 劉海波.大跨度連續剛構橋中跨高溫合龍技術［J］. 鐵道建筑，2005(5):15-17.

［7］ 李亞林，周瑋.連續剛構橋頂推力計算方法及受力性能分析［J］.交通科技與經濟，2012，9(5):6-8.

［8］ 欒坤鵬，張雪松，高洪如.連續剛構橋合龍頂推力優化計算方法［J］.魯東大學學報:自然科學版，2011，27(1):92-96.

［9］ 潘國兵，劉毅.多跨連續剛構橋主梁合龍方案研究及對應頂推力計算［J］.公路交通科技:應用技術版，2012(91):193-198.