自適應差分進化算法在PMSM電機控制器中的應用

王 杰 ，胡玉純，畢浩洋

(鄭州大學 電 氣工程學院，河南 鄭 州450001)

0 引言

永磁同步電機(Permanent Magnet Sync hronousMotor，PMSM)具有體積小、效率高、功率因數高、起動轉矩大、溫升低等特點，能夠實現裝置的轉速和位置的精確控制，廣泛應用于機械加工、電力拖動等裝置［1］.

由于PMSM電機的非線性、多耦合等特性以及工作環境的變化，常規的矢量控制方式不能夠保證轉速調節的快速性和準確性.為了改善PMSM轉速控制系統的動態性能，許多智能控制算法相繼被引入到PMSM電機轉速控制領域［2］.這些算法在一定程度上改善了系統的性能，但各自都存在著一定的局限性，神經網絡隱含層數以及各層節點數沒有系統的確定方法，遺傳算法收斂速度慢且操作復雜［3］.差分進化(Differential E-volution，DE)算法收斂速度快、進化參數少、結構簡單且泛化能力強，在各個領域獲得廣泛應用［4］.但標準差分進化中難以確定合適的變異率，變異率過大會導致搜索速度慢，不易收斂到最優解，變異率過小則容易出現“早熟”現象［5］.因此筆者將自適應差分進化算法(Self-Adaptive Differential Evolution，SADE)應用到PMSM電機控制當中，改善了PMSM轉速調節的動態性能和靜態性能，并通過Matlab/simulink仿真驗證了方案的可行性.

1 永磁同步電機數學模型

永磁同步電機結構復雜并且高度非線性.采用PMSM的d-q軸數學模型［6］，不僅能夠同時分析PMSM的穩態特性和暫態特性，而且能夠簡化分析過程［7］.通過如下假設:忽略空間諧波，磁路不飽和，不計鐵心損耗，忽略渦流和磁滯損耗，可以得到PMSM的d-q軸數學模型.此時，我們可得PMSM的d-q軸磁鏈方程為

式中:Ψr為轉子在定子上的磁鏈耦合;Ld，Lq分別為PMSM的d軸和q軸電感;id為定子電流矢量的d軸分量;iq為定子電流矢量的q軸分量.

在PMSM的d-q軸坐標系下，定子電壓方程可以表示為

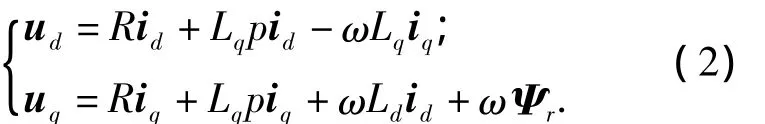
式中:ud為定子電壓矢量us的d軸分量;uq為定子電壓矢量us的q軸分量;ω為轉子的角頻率;p為微分算子.

PMSM電機的電磁轉矩方程為

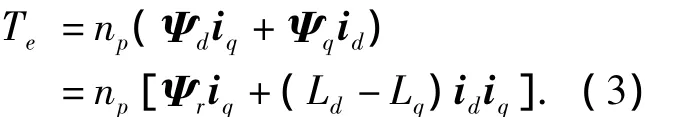
式中:np為電機極對數;(Ld-Lq)idiq為磁阻轉矩.

當PMSM運行在恒轉矩區域時，通過將定子電流矢量全部控制到交軸上(iq=is)，可以使定子電流全部用于產生電磁轉矩.此時，可得PMSM電機的磁鏈方程:

電壓方程:

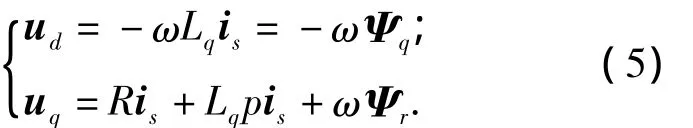
電磁轉矩方程:

由于永磁同步電機的轉子為永磁體，即Ψr為固定值，從上述公式可以看出:電磁轉矩為定子電流的npΨr倍.因此，調節定子電流就能夠準確地輸出期望的電磁轉矩，從而獲得優良的調速特性.

2 自適應差分進化算法

標準差分進化是一種類似于遺傳算法但性能更優越的算法，它采用實數編碼，通過貪婪準則不斷選擇群內個體［8］;它在變異步驟上采用差分策略，算法的優化速度和全局優化能力有了較大提高.但標準差分進化算法的進化參數為固定值，不能隨著優化過程的發展而自適應調整.為提高算法的快速性和魯棒性，筆者提出了一種進化參數能夠動態調整的自適應差分進化算法.

2.1 初始化

自適應差分進化算法開始前需要將種群初始化為可行域內的隨機量NP為種群規模.種群中每個個體表示為:xi，G(i=1，2，…，Np)，其中:i為個體在群體中的位置;G為進化的代數.在尋找最優解之前，要對種群進行初始化.即從參數變量的界限中隨機獲取一個值:

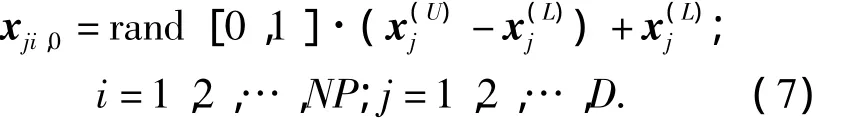
2.2 變異

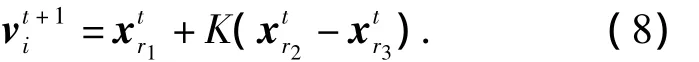
式中:r1，r2，r3∈{1，2，…，Np}兩兩之間不相等并且不等于i為第t代基向量)為第t代的差分向量;K∈［0，1］為變異因子.

2.3 交叉

為增加種群的多樣性，通過對xti和變異得到的新個體 vti+1進行交叉運算，得到實驗個體，即

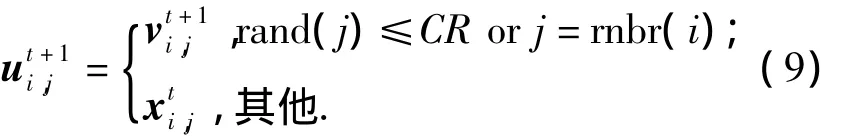
式中:rand(j)為取值范圍是［0，1］的均勻隨機數;CR為取值在［0，1］范圍內的交叉因子;rnbr(i)為一個隨機量，且 rnbr(i)∈{1，2，…，D}.

2.4 選擇

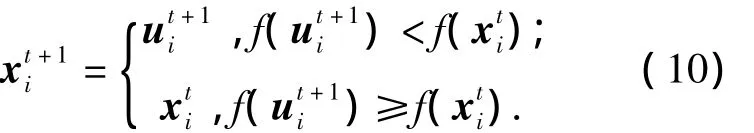
2.5 進化參數的自適應調整

在標準差分算法進化尋優過程當中，種群規模NP、變異因子K以及交叉因子CR共3個參數都為固定值，參數值選擇的合適與否對計算的過程和結果有很大影響［9］.其中，變異因子K的最優值難以確定，如果K的值選取過大，搜索步長太大，容易形成振蕩，不易收斂到全局最優解;如果K的值選取過小，搜索步長太小，搜索過程緩慢并且易于收斂到局部最優解［10］.仿真實驗表明，采用能根據搜索階段作自適應調整的變異因子K，即在開始階段選取較大的K值，在搜索后期選取較小的K值，既能保證算法的快速性，又能避免陷入局部最優解.自適應的變異因子如下:

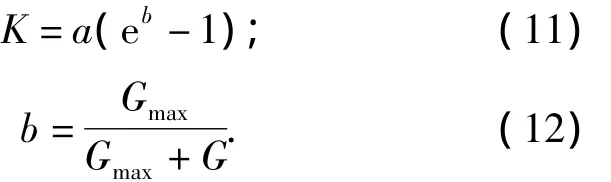
式中:Gmax為最大進化次數;G為當前進化次數;參數 a取值范圍為［0.2，0.6］.

3 自適應差分進化PID控制器

3.1 控制系統結構

SADE-PID控制系統的結構如圖1所示.整個系統采用閉環控制的方式連接，將采樣得到的參數u(k)、e(k)、n(k)作為自適應差分進化算法的輸入，輸出為經過優化的PID參數.PID控制器輸出SVPWM的參考電壓，通過SVPWM調制方法產生驅動電機運轉的電壓，最終實現PMSM電機轉速的高效控制.

3.2 適應度函數選取

準確的適應度函數是自適應差分進化算法應用于控制系統的基礎，它是進化過程中個體優劣程度的評價標準，保證了種群不斷向最優的方向進化，最終實現系統動態特性和靜態特性的最優化.為綜合全面地評價控制器的動態性能指標，應建立包含多個系統參數的目標函數.因此，可將系統的各個參數加權后列入目標函數表達式當中.最終選取的目標函數為

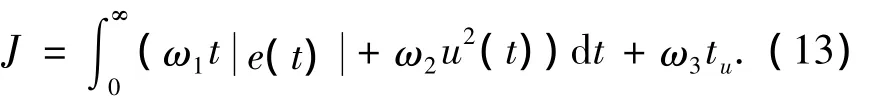
式中:e(t)為轉速誤差;tu為上升時間;u(t)為控制器輸出;ω1、ω2、ω3為權值.

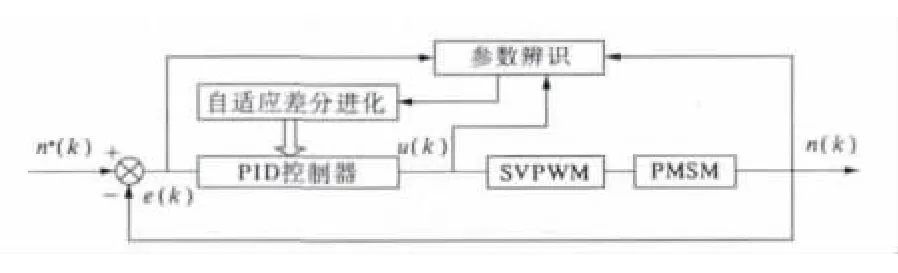
圖1 SADE-PID控制系統結構圖Fig.1 SADE-PID control system diagram

良好的控制效果應當是超調量盡量小且調節時間盡量短，即適應度函數與目標函數J成反比，故在實際應用中選擇適應度函數為

式中:10-10用于防止分母為零.

3.3 SADE-PID參數優化步驟

(1)參數選擇.選擇自適應差分進化算法需要確定的各個參數，種群規模NP、變異因子K、交叉因子CR、最大進化次數Gmax、參數a和算法終止條件.

(2)根據種群規模NP和最大進化次數Gmax，隨機初始化種群.

(3)評估隨機初始化的種群，得到種群內部各個個體的適應度函數值.

(4)初次判斷是否符合終止條件.若符合，則算法結束，將此時的最優解輸出;若不符合，進行第(5)步.

(5)按照相應的變異因子和交叉因子，執行變異和交叉操作，產生試驗向量.

(6)比較目標向量xi，G和試驗向量，按照貪婪準則進行選擇，產生新種群.

(7)重新評價新種群.若達到最大進化次數Gmax或適應度函數值小于閥值λ=10-6，則終止進化;否則，進化代數加1并轉到第(4)步繼續運行.

4 仿真研究

利用Matlab/simulink構建系統模型，驗證控制算法的性能.根據需要選取PMSM電機，其參數如表1所示.

表1 PMSM電機參數Tab.1 PMSMmotor parameters

根據永磁同步電機的結構特性，在Matlab/simulink中建立系統的控制模型，設置自適應差分進化的相關參數，然后進行仿真分析.設定種群規模為NP=30，種群中每個成員含有3個參數變量:KP、KI和 KD.取變異因子 K=0.08，交叉因子CR=0.90，參數 a=0.35.借鑒 Ziegler-Nichols整定方法得到的結果，將種群中各成員參數變量的邊界條件設定為:Kp∈［0 20］、KI∈［0 1］和KD∈［0 1］;適應度函數中的 ω1、ω2、ω3取隨機值.

設置適當的參數后，進行仿真分析，得到PMSM在不同情況下的響應曲線.經過自適應DE算法優化PID參數的PMSM轉速響應曲線與標準DE優化PID參數轉速響應曲線的對比如圖2所示;兩種控制方式下對轉矩擾動的響應曲線對比如圖3所示.

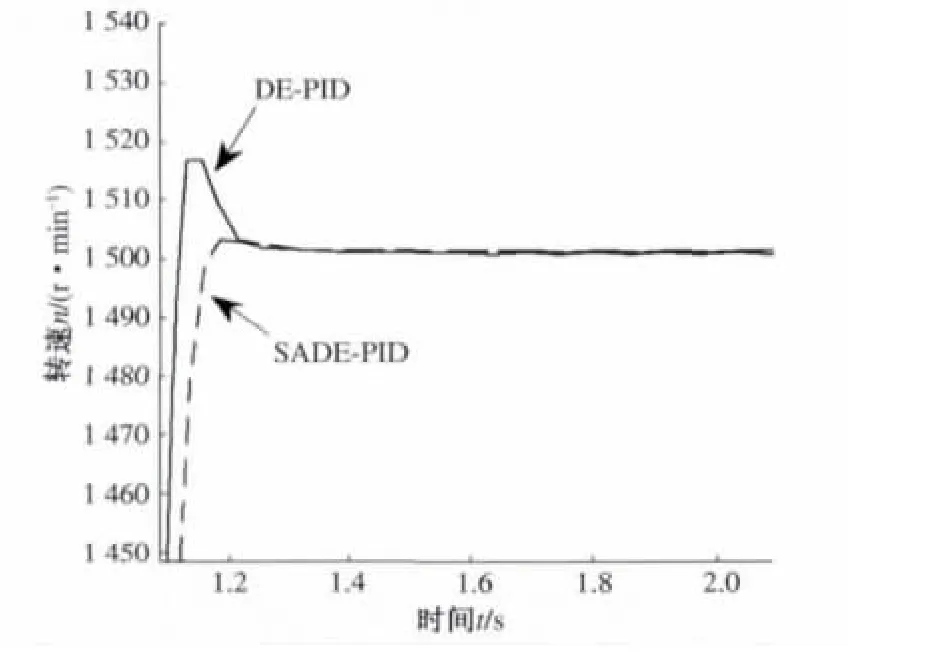
圖2 階躍輸入的轉速響應Fig.2 Speed response to a step input

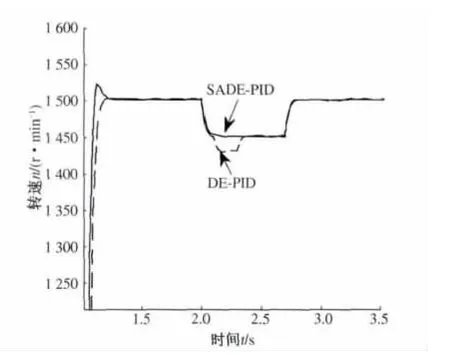
圖3 轉矩擾動時的轉速響應Fig.3 The torque disturbances speed response

通過對比分析圖2和圖3可知:PMSM轉速控制系統的PID參數經過自適應差分進化算法優化以后，不僅超調量大幅減小，響應時間明顯縮短，控制精度提高，而且能夠實現轉速的平穩控制，抗干擾能力也大大增強.系統的動態特性和靜態特性與標準差分進化算法PID整定方法相比，都有顯著的改善，體現了利用自適應差分進化算法優化PMSM轉速控制系統參數的可行性和有效性.

5 結束語

提出了一種利用自適應差分進化算法優化PID參數的永磁同步電機轉速控制系統，并且詳細描述了算法的實現步驟.仿真實驗表明，由于自適應差分進化算法的快速收斂性和強大的全局尋優能力，PMSM電機轉速控制系統的動態特性和靜態特性都得到了顯著改善.這體現了將自適應差分進化算法引入到PMSM轉速控制領域的實際意義.

［1］ 王秀和.永磁電機［M］.北京:中國電力出版社，2011:5-8.

［2］ 楊華芬，楊有，尚晉.一種改進的進化神經網絡優化設計方法［J］.鄭州大學學報:工學版，2010，31(5):116-120.

［3］ DAVID B F.Evolutionary computation:Toward a new philosophy of machine intelligence［M］.NewYork:IEEE Press，2000:185-200.

［4］ 雷小宇，樓樸根.基于差分進化的多機器人路徑規劃［J］. 計算機仿真，2011，28(1):10-13.

［5］ 王艷宜.改進差分進化算法及其應用［J］.機械設計與研究，2010，26(5):13-16.

［6］ 張永春.高性能PMSM矢量控制系統設計與實現［J］.制造業自動化，2012，34(11):122-125.

［7］ ZHANG Ying-cai，ZHU Jia-gang.Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency［J］.IEEE Transactions on Power Electronics，2011，26(1):235-248.

［8］ STORN R，PRICE K.Differential evolution-A simple and efficientadaptive scheme for global optimization over continuous spaces［R］.Berkeley:University of California，2006.

［9］ DASS，SUGANTHAN P N.Differential evolution:A survey of the state-of-art［J］.IEEE Transactions on Evolutionary Computation，2011，15(1):4-31.

［10］熊偉麗，許文強，徐保國.基于差分進化算法的Wiener模型辨識［J］.控制工程，2012，19(5):900-904.