一種等幾何形狀優化的網格更新方法

□ 李 楊 □ 張衛紅 □ 蔡守宇

西北工業大學 現代設計與集成制造技術教育部重點實驗室 西安 710072

結構形狀優化旨在通過修改結構內外邊界幾何形狀，改善結構特性（如降低應力集中、提高剛度、減輕結構質量），主要包括三步：參數化幾何模型的建立；結構響應分析和靈敏度計算；優化算法的實現。在優化過程中，用于描述結構幾何形狀的參數作為設計變量，結構質量與響應（如應力、柔順度、頻率等）作為目標函數和約束。

傳統的形狀優化方法采用計算機輔助幾何設計（CAD）進行幾何建模，即利用Bezier、B樣條或非均勻有理B樣條（NURBS）參數化描述。由于CAD模型無法直接用于有限元分析（FEA），需要劃分有限元網格后 進 行 分 析 和 優 化［1］， 幾 何 模 型 （CAD） 和 分 析 模 型（FEA）相互孤立，如圖 1（a）所示。

IGA方法將NURBS基函數不僅用于參數化幾何建模，而且用于力學場計算［2］，實現了幾何模型（CAD）、分析模型（IGA）和優化模型的無縫連接，如圖1（b）所示。由于CAD模型直接用于等幾何分析，幾何形狀的精確表示使分析精度提高。目前，基于IGA的形狀優化已被成功應用于平面線彈性問題［3,4,5］、三維線彈性問題［6］、梁結構［7］和振動腔問題［8］。 基于 T 樣條和Coons曲面的幾何參數化方法也被應用于等幾何形狀優化中［9,10］。

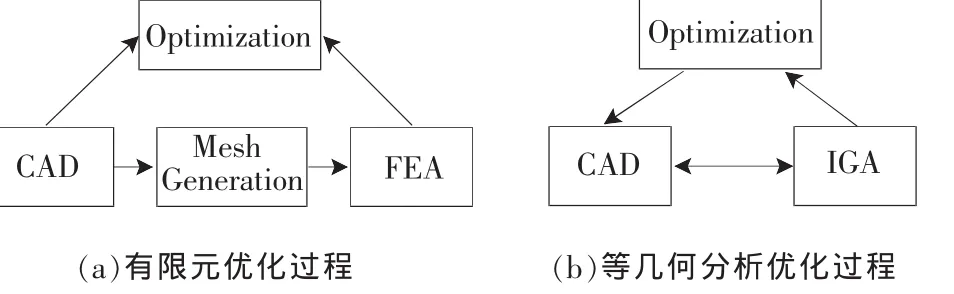
▲圖1 優化過程的比較示意圖

然而，優化迭代過程中NURBS控制點的大幅變化，時常使相鄰控制點距離過近或過遠，甚至出現網格重疊畸形，需要在迭代過程中進行網格更新。文獻［3］采用內部控制點的位置與邊界控制點的位置成固定比例的方法控制網格，這種方法雖然簡單但缺乏通用性。文獻［9］采用虛擬位移載荷法，把邊界控制點的變化量作為一個彈性輔助系統的位移邊界載荷處理，通過求解相應的線性方程組得到內部控制點的變化量。方法較為通用，但是每次迭代之后相當于要額外進行一次有限元分析，效率較低。

本文借鑒文獻 ［11］空氣動力學中的網格調整策略，采用基于NURBS控制點間距的網格更新方法，進行IGA形狀優化。首先簡要介紹IGA方法、相應的形狀優化模型，然后建立網格更新方法，最后給出平面線彈性形狀優化算例。

1 IGA等幾何分析方法

對于平面線彈性問題的IGA離散形式為：

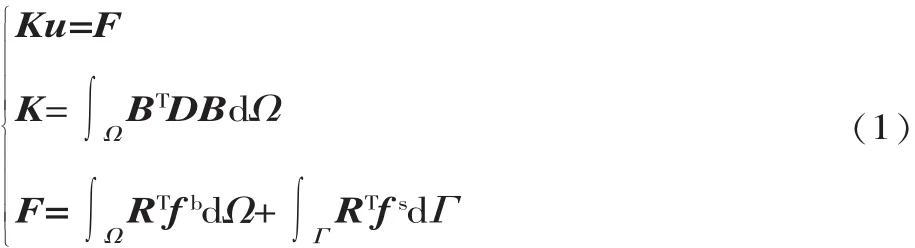
式中：Ku=F為IGA離散的平衡方程；Ω為彈性體幾何域；Γ為面力邊界；K為總剛度矩陣；F為總載荷向量；u為節點位移向量；fb為體力載荷向量；fs為面力載荷向量；D 為彈性矩陣；為基函數矩陣，

上述基函數R可由雙變量NURBS基函數構造得到：

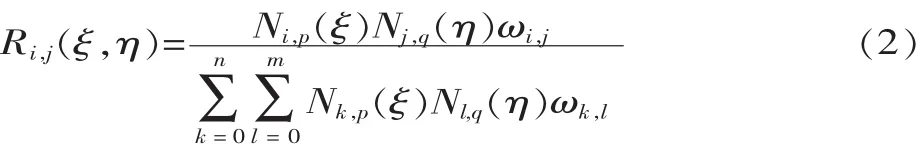
式中：ξ、η 為 NURBS 節點參數；p、q 為基函數階數；n、m 為基函數個數；ωi，j為權值。

類似于有限元分析，總剛度矩陣和總體載荷向量可以由單元剛度矩陣和單元載荷向量組裝而成。由此可見，等幾何分析得到的離散方程，形式上與有限元分析相同：NURBS控制點對應有限元分析中的節點，NURBS物理空間網格對應有限元分析中的網格，NURBS控制點上的位移對應有限元分析中的節點位移等。

2 基于等幾何分析的形狀優化

2.1 形狀優化模型

形狀優化就是通過改變連續體結構內外邊界形狀以改善結構特性（如減輕結構質量、降低應力集中等）的一種優化過程。基于IGA的形狀優化問題一般可以描述為：

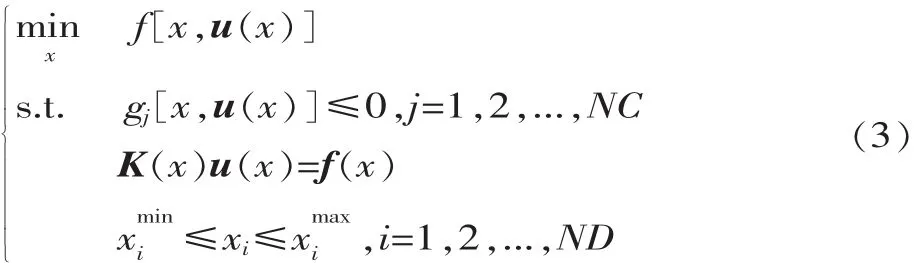
式中：x為與邊界NURBS控制點相關的設計變量；ND為設計變量個數；f和gj分別為目標函數和約束；NC為不等式約束個數。

2.2 網格更新方法

基于IGA的形狀優化在迭代過程中，常會出現設計變量的大變形。如圖2（a），優化迭代之前NURBS控制網格中控制點P在Y的正方向有大變形，那么迭代之后可能會出現網格重疊［如圖2（b）］。這樣變形之后的網格是畸形網格，無法繼續進行分析。為保證網格的協調性，采用一種基于控制點間距的網格更新方法。

▲圖2 NURBS控制網格大變形示意圖

考慮四分之一厚壁圓筒截面的NURBS控制點網格，如圖3所示。選擇實心圓代表的控制點作為設計變量，僅限制其在虛線（邊界法向）的方向上擾動。為方便說明，將圖中所示控制網格中的虛線上“一列”提取出來說明。 P0，P1，...，Pm為 m+1 個控制點的位置，其中，P0為邊界設計變量控制點（Variable Control Point），Pm為固定控制點（Fix Control Point），其余為連接控制點（Linked Control Point）。ΔP0，ΔP1，...，ΔPm為對應的控制點變形量，di=dist（Pi，Pi-1）（1≤i≤m）為相鄰兩控制點之間的距離。建立如下關系：

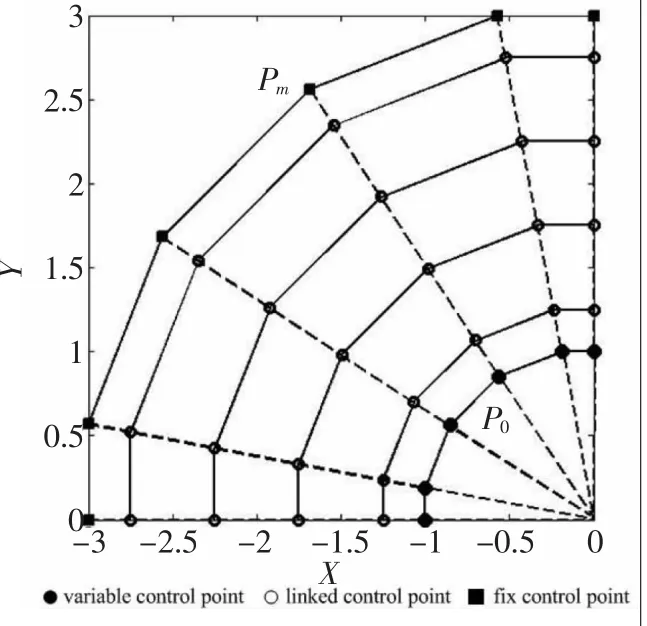
▲圖3 網格更新方法示意圖

故有：從而：

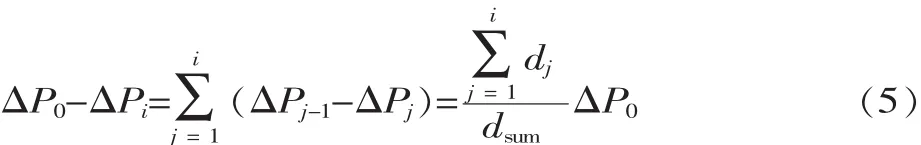
下面給出式（7）的3條性質：

性質 1：當 i=m 時，ΔPm=CmΔP0=0，這與 Pm為固定控制點相符。

性質 2：若 ΔPi1=Ci1ΔP0，ΔPi2=Ci2ΔP0，則有當 i2＞i1 時，Ci2＜Ci1，所以 ΔPi1＞ΔPi2，說明:距離邊界可變控制點P0越近的點，變形量越大；距離P0越遠的點，變形量越小。

性質 3：當 i2＞i1時，Pi2＞Pi1， 考察擾動后兩點Pi1+ΔPi1，Pi2+ΔPi2的位置關系，有：

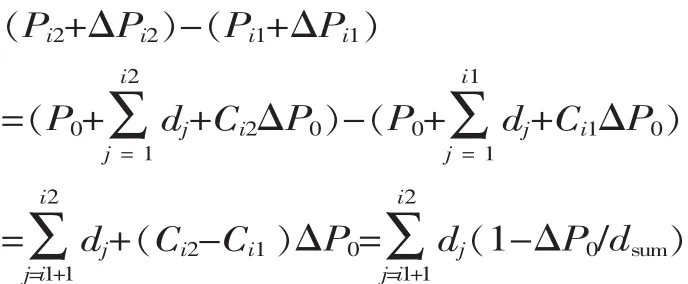
又 ΔP0＜dsum，故（Pi2+ΔPi2）-（Pi1+ΔPi1）＞0 即 Pi2+ΔPi2＞Pi1+ΔPi1。也就是任意兩控制點在網格更新之后，都保持變形前的拓撲關系，不會出現網格重疊現象。

3 數值算例

基于上述的網格更新方法，下面給出等幾何形狀優化的數值算例。優化算法采用移動漸近線算法（MMA）［12］。 收斂準則為：

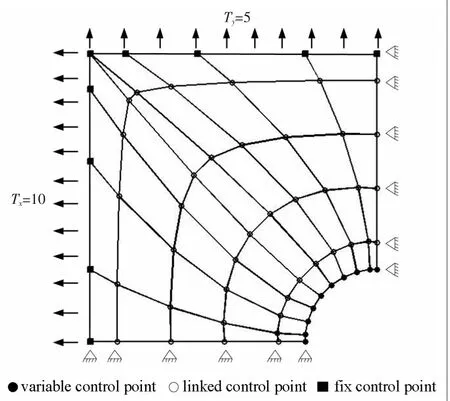
▲圖4 四分之一帶孔平板初始NURBS模型

▲圖5 優化前后von-Mises應力云圖對比

式中：fi為第i次迭代之后的目標值；f0為目標初始值。

本文中控制點權值在優化過程中保持不變。考慮平板應力集中問題，由于對稱性，僅考慮四分之一帶孔平板。問題初始模型定義如圖4所示，板兩邊受均布拉力，楊氏模量為210 GPa，泊松比為0.3，平板厚度為1 mm。在體分比99%的約束下，優化目標為最大von-Mises應力最小。初始形狀下von-Mises應力云圖如圖5（a）所示，優化后形狀和von-Mises應力云圖如圖5（b）所示。初始最大von-Mises應力為27.245 2 MPa，優化后為15.744 2 MPa，應力集中明顯降低。

4 結論與展望

等幾何分析通過NURBS將CAD、FEA和結構形狀優化結合起來，省去了繁瑣的模型轉換，擁有諸多優點，有著極大的發展前景。此外，等幾何分析對于解決一些高階問題（如板殼問題）具有獨特的優勢。本文采用一種基于NURBS控制點間距的網格更新方法，成功應用于等幾何形狀優化。數值算例表明，此方法簡單有效，下一步將結合此方法進行三維的等幾何形狀優化研究，并進一步嘗試等幾何形狀優化在板殼問題中的應用。

［1］ V Braibant and C Fleury.Shape Optimal Design Using B-splines ［J］.Computer Methods in Applied Mechanics and Engineering,1984,44：247-267.

［2］ Hughes TJR,Cottrell JA,Bazilevs Y.Isogeometric Analysis：CAD,Finite Elements,NURBS,Exact Geometry and Mesh Refinement ［J］.Computer Methods in Applied Mechanics and Engineering,2005,194（39-41）： 4135-4195.

［3］ Wall WA,Frenzel MA,Cyron C.Isogeometric Structural Shape Optimization ［J］.Computer Methods in Applied Mechanics and Engineering,2008,197（33-40）： 2976-2988.

［4］ Cho S,Ha S-H.Isogeometric Shape Design Optimization：Exact Geometry and Enhanced Sensitivity［J］.Structural and Multidisciplinary Optimization,2009,38（1）： 53-70.

［5］ Xiaoping Q.Full Analytical Sensitivities in NURBS Based Isogeometric Shape Optimization ［J］.Computer Methods in Applied Mechanics and Engineering,2010,199 （29-32）：2059-2071.

［6］ Hassani B,Tavakkoli SM,Moghadam NZ.Application of Isogeometric Analysis in Structural Shape Optimization ［J］.Scientia Iranica,2011,18（4）： 846-852.

［7］ Nagy AP,Abdalla MM,Gürdal Z.Isogeometric Sizing and Shape Optimisation of Beam Structures ［J］.Computer Methods in Applied Mechanics and Engineering,2010，199（17-20）： 1216-1230.

［8］ Manh ND,Evgrafov A,Gersborg AR,et al.Isogeometric Shape Optimization of Vibrating Membranes ［J］.Computer Methods in Applied Mechanics and Engineering,2011,200（13-16）： 1343-1353.

［9］ Ha S-H,Choi K,Cho S.Numerical Method for Sshape Optimization Using T-spline Based Isogeometric Method［J］.Structural and Multidisciplinary Optimization,2010,42 （3）：417-428.

［10］ Qian X,Sigmund O.Isogeometric Shape Optimization of Photonic Crystals via Coons Patches ［J］.Computer Methods in Applied Mechanics and Engineering， 2011，200（25-28）：2237-2255.

［11］ Pandya MJ,Baysal O.Gradient-based Aerodynamic Shape Optimization Using Alternating Direction Implicit Method［J］.Journal of Aircraft,1997,34（3）： 346-352.

［12］ K.Svanberg,The Method of Moving Asymptotes： A New Method for Structural Optimization［J］.International Journal of Numerical Methods in Engineering， 1987，24：359-373.