應用Taylor公式證明相關定理
2013-11-23 06:19:12張學茂王大增楚建亞
衡水學院學報
2013年1期
張學茂，王大增，楚建亞
(泰州師范高等專科學校 機電工程學院，江蘇 泰州 225300)
Taylor公式是《數學分析》《高等數學》中一極其重要的工具，不少專家學者研究了其在求函數的近似值及誤差估計、證明不等式、求函數的極限、極值、判別級數的斂散性、廣義積分的斂散性、行列式的計算，乃至微分方程解等方面的應用[1-5].大多數限于一元函數問題的解決，在定理證明中的應用方面較為罕見，且筆者在長期的教學實踐中發現：由于學生的知識結構與知識點編排先后的限制，許多定理、結論在首次出現時，證明的方法較繁或較抽象，給學生的理解帶來了較大的困難.而學習了Taylor公式后，利用該公式可以較簡易地、定性地證明相關的定理或結論，并能將一元函數的有關結論推廣至多元函數，這樣能加強學生對相關知識的理解，并進行有效的推廣，促進學生知識結構的重組與更新.
1 預備知識
引理1[6]265-266(Taylor定理)若函數 f ( x) 在點 x0處存在 n 階導數，則?x∈u( x0)有
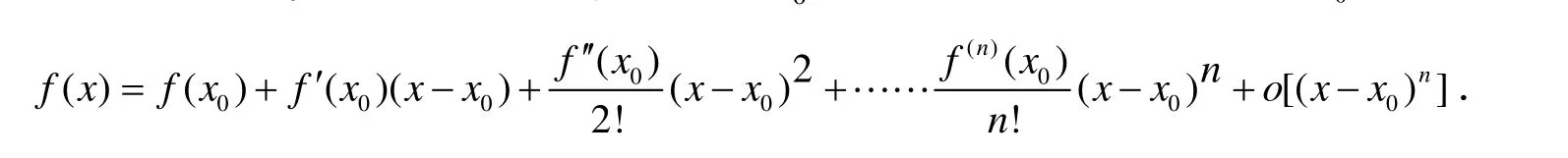
在實際應用中常用用二階的Taylor公式
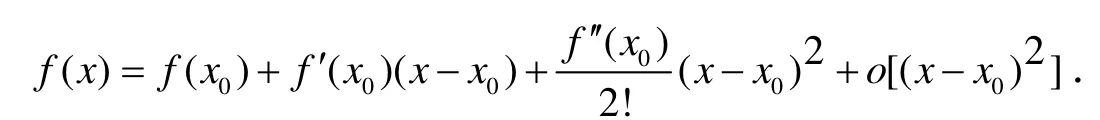
引理2[7]對于任一組不全為零的實數Δx, Δy 有則稱矩陣是半正定的.
定義1[6]296f( x)為定義在區間I上的函數，對I上任兩點 x ,x和實數?λ∈（0,1）總有12f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)，則稱f(x)為區間I上的凸函數，反之稱為凹函數.
定義2[8]設 D ? Rn是凸集，函數f( x) 定義在D 上，?λ∈（0,1）及任意兩點 p ,p∈D 恒有12 f(λ p1+(1-λ)p2)≤λf (p1)+(1-λ) f (p2)，則稱 f ( x) 為 D 上的凸函數，反之稱為凹函數.
定義3[6]236f( x) 為在區間I上有定義，若x∈I ，且存在 u (x)?I ，? x ∈ u ( x)總有 f ( x)≤f(x)(或0000 f( x) ＞ f( x0))，則稱 x0是函數 f ( x)的極大值點(極小值點)， f (x0)是函數 f ( x )的極大值(極小值).(類似的可定義多元函數的極值).
