關于群的冪自同態(tài)的一個注記

周建新,陳敬華,黃振華

(湖北師范學院 數(shù)學與統(tǒng)計學院， 湖北 黃石 435002)

1 引言及有關定義

設G是一個群,e是群G的單位元,|G| 表示集合G所含元素的個數(shù),Z(G) 表示群G的中心,N≤G表示N是群G的子群.gcd(m,n) 或(m,n) 表示整數(shù)m,n的最大公因數(shù).

設f:G→G是群G的自同態(tài)，滿足f(x)=xn(?x∈G) ，即對任意的x,y∈G， (xy)n=xnyn. 眾所周知, 當n=2 和-1時,G是一個交換群(見[1～2]). 一個自然的問題被提出來:除上述2和-1外,是否還存在整數(shù)n使得當(xy)n=xnyn時,G是一個交換群? 更一般地, 設M={n|f:G→G是群G的自同態(tài)，滿足f(x)=xn,?x∈G},Ω={n|當n跑遍M中所有元時,G是一個交換群}, 則M中的元素滿足什么性質?本文對此做了一番探討,得出了如下結果:

定理1 若M={n|f:G→G是群G的自同態(tài)，滿足f(x)=xn，?x∈G} ，M0?M,|M0|=1,則G是交換群當且僅當M0={2} 或者M0={-1} .

定理2 設M={n|f:G→G是群G的自同態(tài)，滿足f(x)=xn, ?x∈G},M0?M且 |M0|>1,則G是交換群當且僅當n取遍M0中所有元時，所有形如n(n-1) 元的最大公因數(shù)為2.

定義1 設G是一個群, 若對任意的x,y∈G,存在n∈Z,使得(xy)n=xnyn, 稱G是一個(n) - 群.

注:任意的群都是(1) 群,易證(2)- 群和 (-1)- 群都是交換群.

定義2 設G是一個群,若對任意的x∈G,xn=e,其中e是群G的單位元, 則稱G是一個冪為n的群.

注:若群G的冪為n,則對任意的整數(shù)k,G既(kn)- 群又(kn+1) - 群.

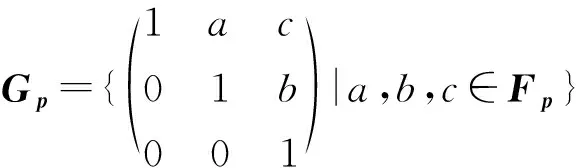
i)Gp按照通常矩陣的乘法構成一個非交換群;

ii)當p是奇素數(shù)時,Gp是一個冪為p的群;

iii)當p=2時,Gp是一個冪為4的群.

注: 由引理易知當p是奇素數(shù)時,Gp既是(pk) - 群又是(pk+1) - 群;當p=2 時,G2既是(4k) - 群又是(4k+1) - 群.

引理2 設M={n|f:G→G是群G的自同態(tài)，滿足f(x)=xn,?x∈G},則

i)對任意的m,n∈M有mn∈M;

ii)n∈M當且僅當1-n∈M.

證 i)是顯然的.下證ii)

若n∈M,則對任意的x,y∈G有(xy)n=xnyn,于是(yx)n-1=xn-1yn-1,從而(yx)1-n=y1-nx1-n,所以1-n∈M.又因為n=1-(1-n) ,所以反之也成立.

引理3 設N={n|xn∈Z(G),?x∈G,n∈M} ,其中M同引理2中的M，則

i)N關于通常整數(shù)的加法運算構成一個群;

ii)若n∈M, 則n(n-1)∈N.

證 i)對任意的m,n∈,x,y∈G有

(xy)m+n=(xy)m(xy)n=xmymxnyn=xmxnymyn=xm+nym+n

從而m+n∈N. 易驗證n∈N當且僅當 -n∈N. 所以N≤G.

ii)若n∈M,則由引理2知1-n∈N,從而n(1-n)∈M.對任意的x,y∈G有yxnyny-1=y(xy)ny-1=(yx)n=ynxn，于是y1-nxn=xny1-n, 即xn與y1-n可交換. 則對任意的x∈G,xn(1-n)既是G中某元的n次冪又是某元的1-n次冪, 所以對任意的y∈G,xn(1-n)與yn和y1-n都可交換, 從而xn(1-n)與y可交換. 由y的任意性知xn(1-n)∈Z(G), 所以n(1-n)∈N.

引理4[5](m1,m2,…,m1)=u1m1+u2m2+…+u1m1,其中m1,m2,…,ml是任意的l個整數(shù),u1,u2,…,ul∈.

2 主要結果及其證明

定理1 若M={n|f:G→G是群G的自同態(tài)，滿足f(x)=xn, ?x∈G},M0?M,|M0|=1,則G是交換群當且僅當M0={2} 或者M0={-1} .

證 充分性易證,下證必要性.

只需證對任意的n∈, 當n≠2 且n≠-1時, 存在非交換群G滿足對任意的x,y∈G, (xy)n=xnyn.事實上, 若n≠2 且n≠-1, 一方面, 當n是一個奇數(shù), 則存在k∈, 使得n=4k+1或n=4k+3, 但由引理1知存在G2是一個非交換(4k+1) - 群, 當n=4k+3且k≠-1 時, 若k=1,則n=7,由引理1,G7是一個非交換(7) - 群, 若k=0,則n=3,由引理1,G3是一個非交換(3) - 群, 若p1,p2…,ps是互不相同的素數(shù),s∈則 ,當某個pi=3(1≤i≤s)時,n=3k1(k1∈) ,由引理1,G3是一個非交換(3) - 群, 當任意pi≠3(1≤i≤s) 時, 則n是一個素數(shù)p,由引理1,Gp是一個非交換(p) - 群. 另一方面,當n是一個偶數(shù), 則存在k∈, 使得n=4k或n=4k+2, 但由引理1知存在G2是一個非交換(4k) - 群, 當n=4k+2且k≠0 時, 若k=1,則n=2×3,由引理1,G3是一個非交換(6) - 群, 若k=-1,則n=-2=-3×1+1,由引理1,G3是一個非交換(-2) - 群, 若p1,p2……ps是互不相同的素數(shù),s∈,則易知是一個素數(shù)p*,由引理1,Gp*是一個非交換(2p*) - 群.定理證完.

到此,我們已知當|M|=1時,G是交換群當且僅當M={2} 或者M={-1} .若|M|>1 時,在文獻[3]和[4]中有結論: 當M包含3個連續(xù)自然數(shù)時,G是一個交換群. 在文獻[4]中有結論: 當M={3,5} 時,G是一個交換群.由引理1知: 存在非交換群G3既是(3) - 群又是(7) - 群, 因此, 當M={3,7} 時,G不一定是一個交換群. 那么M中元滿足什么性質時,G是一個交換群呢? 對此，有如下結論：

定理2 設M={n|f:G→G是群G的自同態(tài)，滿足f(x)=xn,?x∈G} ,M0?M且|M0|>1, 則G是交換群當且僅當n取遍M0中所有元時，所有形如n(n-1) 元的最大公因數(shù)為2.

證明 必要性(反證法):若當n取遍M0中所有元時,所有形如n(n-1) 元的最大公因數(shù)除2以外還有別的因子,不妨設存在p是一個素數(shù),使得2p|n(n-1) .令Up={n|n∈M,2p|n(n-1)|,則當p是奇素數(shù)時,Up={pk,pk+1|k∈} ;當p=2 時U2={4k,4k+1|k∈} . 由引理1知存在非交換的群Gp和G4滿足2p|n(n-1),這與題設矛盾.所以當n取遍M0中所有元時,所有形如n(n-1) 元的最大公因數(shù)只能是2.

充分性 設M={a1,a2,…,al}，所有形如mi=ai(ai-1)元 (1≤i≤l)的最大公因數(shù)是2,則由引理4知存在u1,u2,…ul∈使得2=u1m1+u2m2+…+ulml,由引理3知2∈N, 所以G是一個 (2)- 群,從而是一個交換群.

注:事實上若M={3,5} ,易知gcd(3(3-1),5(5-1)) =2; 若M={n,n+1 ,n+2},因為2=n(n-1)-2(n+1)n+(n+2)(n+1) ,所以gcd(n(n-1),(n+1)n,(n+2)(n+1))=2 .由此可知,定理2是上述特殊情形的推廣.

參考文獻：

[1]Gallian J A.Contemporary Abstract Algebra[M]. Berlin:Springer-Verlag,1990.

[2]Rotman J J.Advanced Modern Algebra[M].Beijing:Higher Education Press,2004.

[3]Isaacs I M.Algebra[M].Beijing:China Machine Press,2003.

[4]Alperin J L,Bell R B.Groups and Representations[M].New York:Springer-Verlag,1995.

[5]Nathanson M B.Elementary Methods in Number Theory[M].New York:Springer-Verlag,2003.