熱化學非平衡模型和表面溫度對氣動熱計算影響分析

董維中，丁明松，高鐵鎖，江 濤

（中國空氣動力研究與發展中心 計算空氣動力研究所，四川 綿陽 621000）

0 引 言

高超聲速飛行器在大氣層飛行過程中，不僅存在高熱流的氣動熱環境問題，還存在嚴重的高溫氣體效應／非平衡效應問題，這就給高超聲速飛行器熱防護設計和氣動設計增加非常大的困難。在這種情況下，準確預測高超聲速飛行器氣動力特性和表面氣動熱環境就非常關鍵。

對高溫氣體效應／非平衡效應問題研究越來越得到重視，國內外建立了有關的計算軟件和發表了相當多論 文［1－8］。2009 年 前 后，意 大 利 航 天 研 究 中 心（CIRA）的 Votta R等人［7－8］，考慮高溫空氣的化學非平衡和熱力學非平衡效應、滑移效應和表面溫度分布，表面溫度取不同的等溫度值或表面熱輻射平衡條件確定的溫度分布，通過數值求解非平衡Navier－Stokes方程的CFD方法（H3NS），對比分析了熱化學非平衡效應、表面催化效應和表面溫度分布對飛行器氣動力／熱特性的影響。

在數值計算氣動熱中，影響準確預測高超聲速飛行器氣動熱環境的因素非常多，不僅有計算網格和計算格式及其邊界處理方法，還有氣體模型、表面溫度和表面催化特性等等。在氣體模型中，不僅有完全氣體模型和化學反應混合氣體模型，還有氣體熱力學模型。在化學反應混合氣體模型中，常用的有5組分、7組分和11組分空氣化學反應模型。在這些影響準確預測高超聲速飛行器氣動熱環境因素中，目前國內外對空氣化學反應的組分模型、熱力學非平衡模型和表面溫度對氣動熱的計算結果的影響規律還不是非常清楚，在高馬赫數和熱化學非平衡條件下，氣動熱數值隨表面溫度變化有什么特征，這些問題都需要深入分析研究。

本文考慮高溫空氣化學反應效應和熱力學非平衡效應，利用自主開發的氣動物理計算軟件系統（AEROPH）中的高超聲速飛行器高溫氣體／非平衡效應流場計算軟件（AEROPH＿Flow），開展熱化學非平衡氣動熱數值計算，分析高溫空氣化學反應的組分模型、熱力學非平衡模型和表面催化特性對氣動熱的計算結果的影響，考察在高馬赫數和熱化學非平衡條件下氣動熱數值隨表面溫度的變化特征，提升準確預測高超聲速飛行器氣動熱環境的能力。

1 非平衡流場控制方程和計算方法

控制方程是三維熱化學非平衡Navier－Stokes方程，無量綱化形式如下［9－10］：

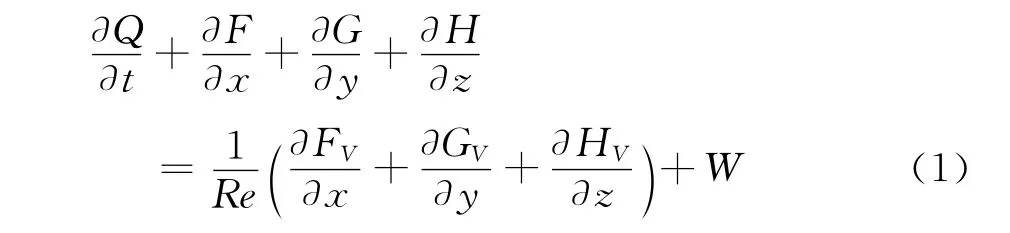
其中，

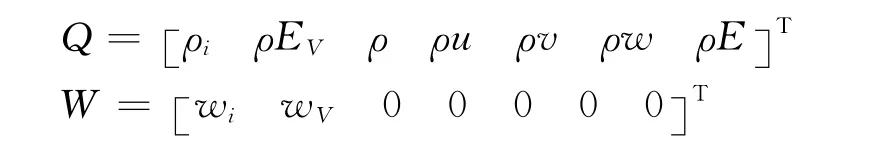
這里i＝（1，2，…，N），N是所考慮的組分方程數。ρi是組分i的密度，EV是分子組分的總振動能量，Re是Reynolds數，wi和wV是化學非平衡源項和振動非平衡能量源項。

對于熱化學非平衡流動情況，狀態方程和能量關系式如下［9－10］：

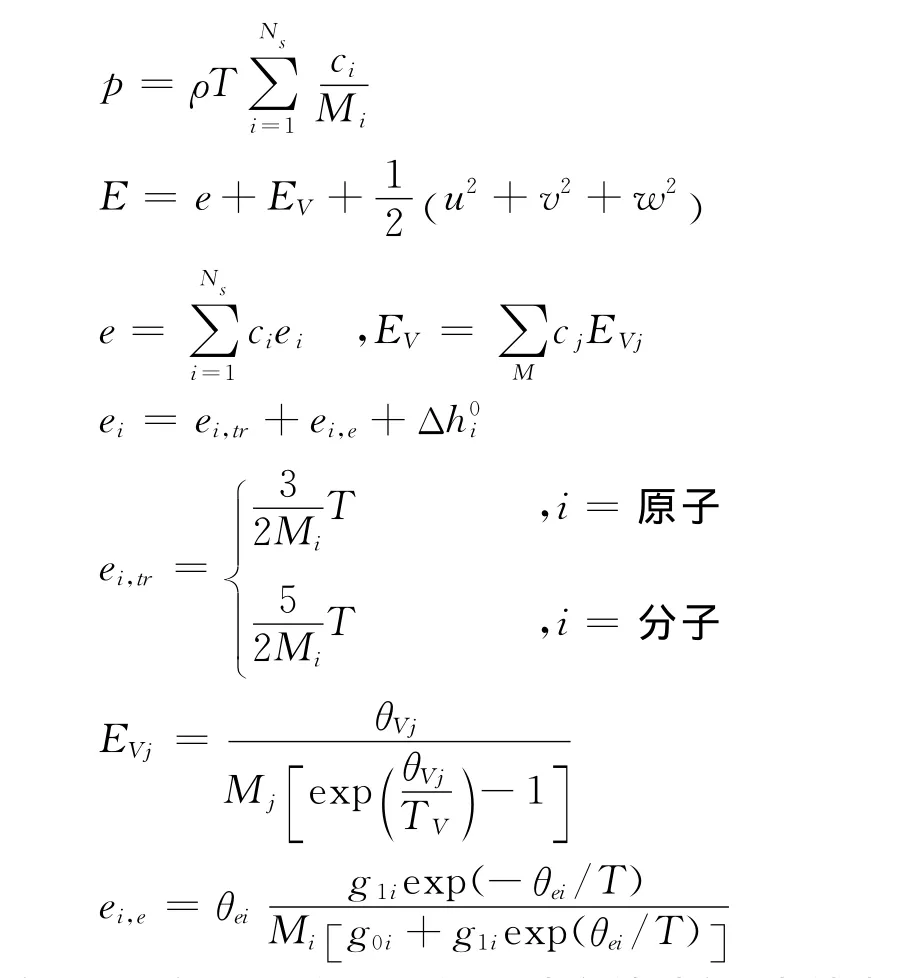
這里ei，tr和ei，e是組分i的平動和轉動能、束縛電子的激發能。θVj是組分j的振動特征溫度，g0i和g1i是組分i的束縛電子第0和第1能級的簡并因子，θei是第一能級的特征溫度。Δ是組分生成能。空氣組分的物理化學數據見文獻［9－10］。

對于化學非平衡流動情況，在控制方程中去掉振動非平衡能量方程和相關項，狀態方程和能量關系式如下［9－10］：

完全氣體的控制方程和狀態方程見文獻［9］。方程（1）采用全隱式的對稱型TVD格式進行差分離散，粘性項用中心差分格式離散。

2 空氣化學反應模型

較常用的空氣化學反應模型有5組分（O2，N2，NO，O，N）、7組分（O2，N2，NO，O，N，NO＋，e）和11組分（O2，N2，NO，O，N，NO＋，e，O＋2，N＋2，O＋，N＋）的模型。在本文研究中，選用了5組分、7組分和11組分的Dunn－Kang空氣化學反應模型。

3 熱力學非平衡模型

對于熱力學非平衡，只考慮振動非平衡效應，考慮振動能量非平衡的組分有O2，N2，NO，NO＋，O＋2和等分子組分。為了減少控制方程數量，振動非平衡效應考慮一個振動溫度。振動非平衡能量源項有如下形式：

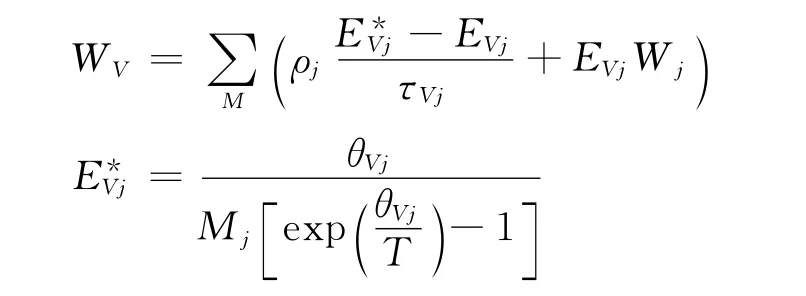
這里、EVj和τVj分別是分子組分j的平衡振動能、非平衡振動能和振動能松弛的特征時間，τVj具體計算公式計算見文獻［9－10］。

4 氣動熱計算方法

對于完全氣體模型，表面熱流計算公式為：

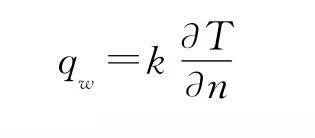
對于化學非平衡氣體模型，表面熱流由對流熱流和組分擴散熱流兩部分組成，計算公式為：

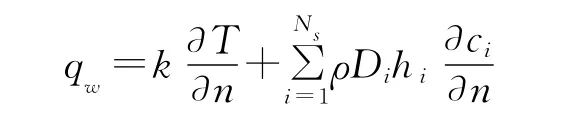
對于熱化學非平衡氣體模型，表面熱流由平動項的對流熱流、振動項對流熱流和組分擴散熱流三部分組成，計算公式為：

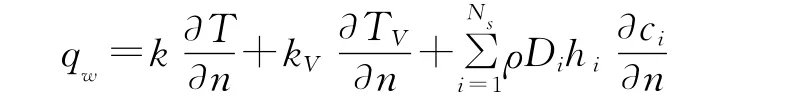
這里k和kV是平動項和振動項熱傳導系數。hi和Di是組分i的焓和擴散系數。對于完全非催化條件，有＝0；對于完全催化條件，有ciw＝ci∞（來流條件）。

5 空氣化學反應模型和熱力學模型對氣動熱計算影響的分析

針對高超聲速飛行器，我們建立了氣動物理計算軟件系統，并開展了大量的驗證與確認工作，在高溫氣體／非平衡效應流場計算軟件方面，開展了大量的與國外文獻［11－13］以及國內外的飛行試驗、地面試驗和理論計算的結果對比分析工作［9－10，14－17］。

計算模型：球頭模型，RN＝35mm；計算狀態：H＝55km，M＝20；熱力學非平衡模型：一溫度模型（T）和兩溫度模型（T－Tv）；空氣化學反應模型：5組分、7組分和11組分化學反應模型；表面條件：Tw＝300K，完全催化（FCW）和完全非催化（NCW）。

圖1給出了不同組分空氣化學反應模型的熱流分布，從圖中可以看到，7組分模型和11組分模型計算的熱流分布幾乎沒有差別，5組分模型計算的熱流值偏小，在M＝20和完全催化條件下熱流偏小13%左右，原因可能是5組分模型沒有考慮電離效應。圖2給出了不同熱力學模型的熱流分布，從圖中可以看到，不同熱力學模型計算的熱流分布有一定差異，最大差異在10%左右，兩溫度模型計算的熱流值高于一溫度模型計算的熱流值。從總的來看，在同樣催化條件下，不同組分空氣化學反應模型和不同熱力學模型計算的熱流分布差異主要集中在球頭模型的駐點區域，后面差別較小。

6 表面溫度對氣動熱計算影響的分析

計算模型：球錐模型，RN＝35mm，θ＝5°，L＝2m；計算狀態：H＝60km和55km，M＝20；熱力學非平衡模型是一溫度模型，空氣化學反應模型是7組分模型；表面條件：Tw＝300K，800K，1500K，2000K，完全催化和完全非催化。

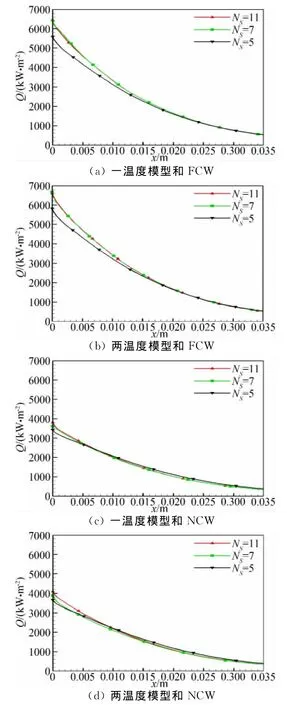
圖1 不同組分空氣化學反應模型的熱流分布（NCW和FCW）Fig.1 Distribution of heat transfer rate on the hemisphere for different species chemical reaction models（NCW and FCW）

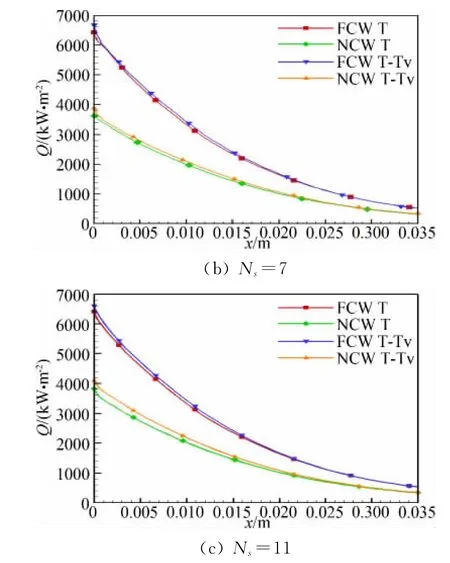
圖2 不同熱力學模型的熱流分布（NCW和FCW）Fig.2 Distribution of heat transfer rate on the hemisphere for different thermodynamic nonequilibrium models（NCW and FCW）

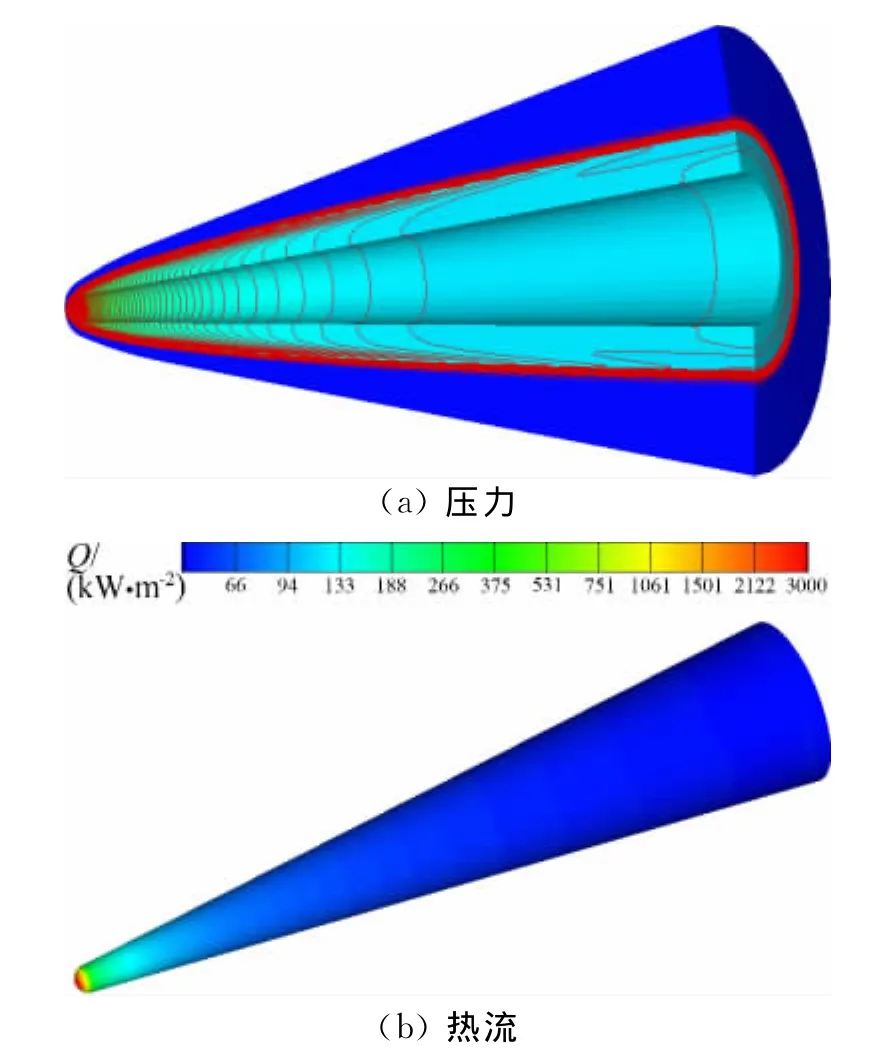
圖3 球錐模型H＝55km的壓力和表面熱流分布云圖Fig.3 Contours of pressure and heat transfer rate for the sphere－cone body at the altitude of 55km

圖3給出Rn＝3 5mm了球錐模型H＝5 5km、M∞＝18、Tw＝300K、Ns＝7、NCW 狀態熱流分布云圖，從圖可以看出：高熱流區域和空氣化學反應最強區域在球錐體的頭部區域，在后身部區域熱流低和空氣化學反應弱。

圖4給出了球錐模型駐點熱流和球錐末端熱流及其成分隨表面溫度變化的分布。從圖可以看出：（1）不同表面溫度計算的熱流分布有一定的差異，在Tw＝300K～800K之間，表面溫度越高，表面熱流越高，在Tw＝800K～2000K之間，隨表面溫度增加，表面熱流先緩慢升高，Tw＝1500K之后，有降低趨勢；（2）表面溫度增加，組分擴散項熱流一直增加，表面溫度從300K到2000K，組分擴散項熱流在總熱流中的百分比從33%左右到40%左右；（3）表面溫度變化對球錐頭部區域熱流值影響大，但對球錐身部區域影響小；（4）表面催化效應對球錐體的頭部區域熱流影響大，對后身部區域熱流影響小。

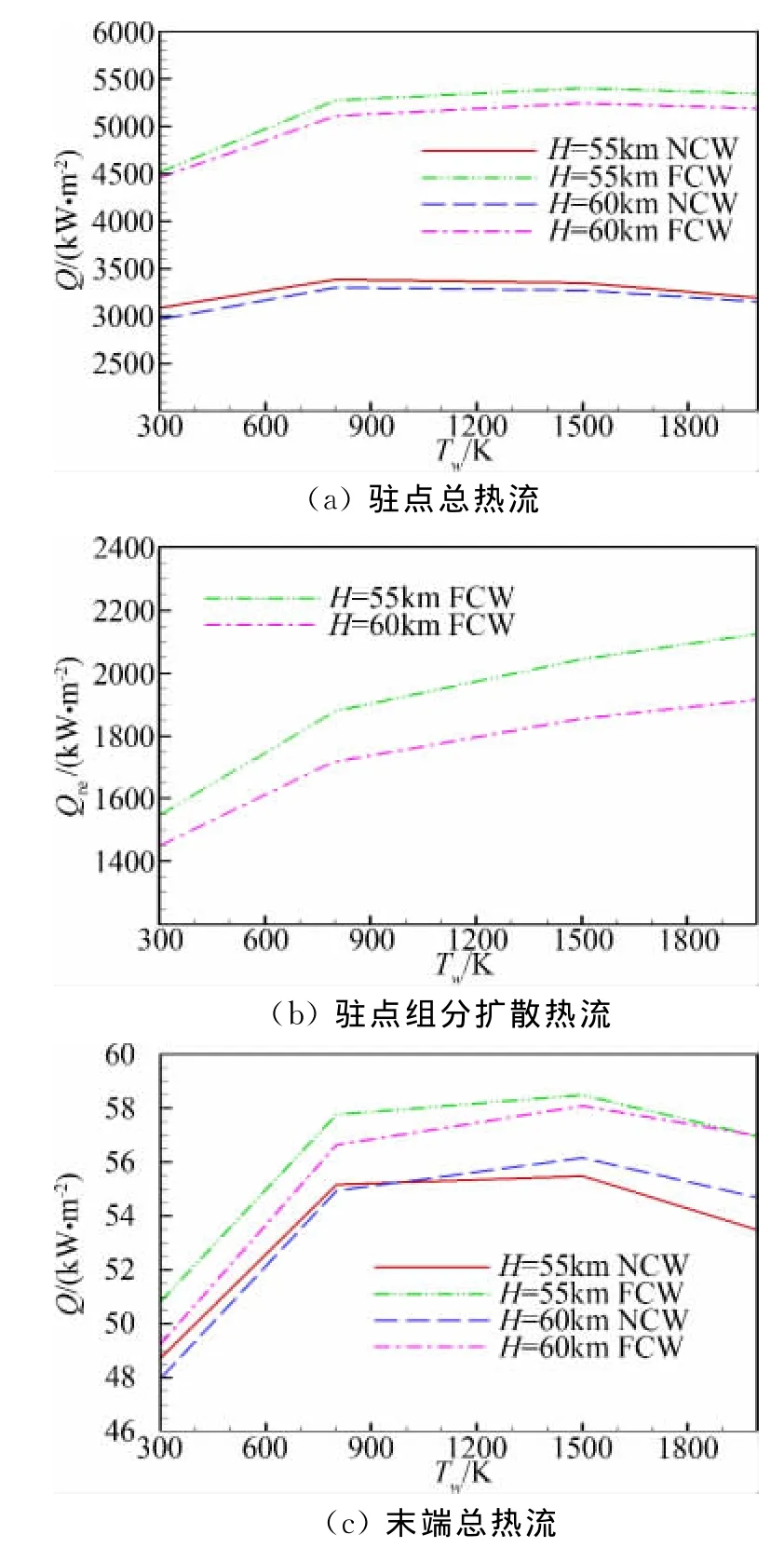
圖4 球錐模型駐點和末端熱流隨表面溫度變化的分布Fig.4 Variation of the heat transfer rate at the stagnational point and the end of the sphere－cone body for different surface temperatures

從分析可以看出：氣動熱隨著表面溫度的變化規律在高馬赫數和非平衡條件下就變得非常復雜，不能再認為氣動熱遵從隨著表面溫度的升高而降低的規律。

7 高升阻比外形不同表面溫度氣動熱計算分析

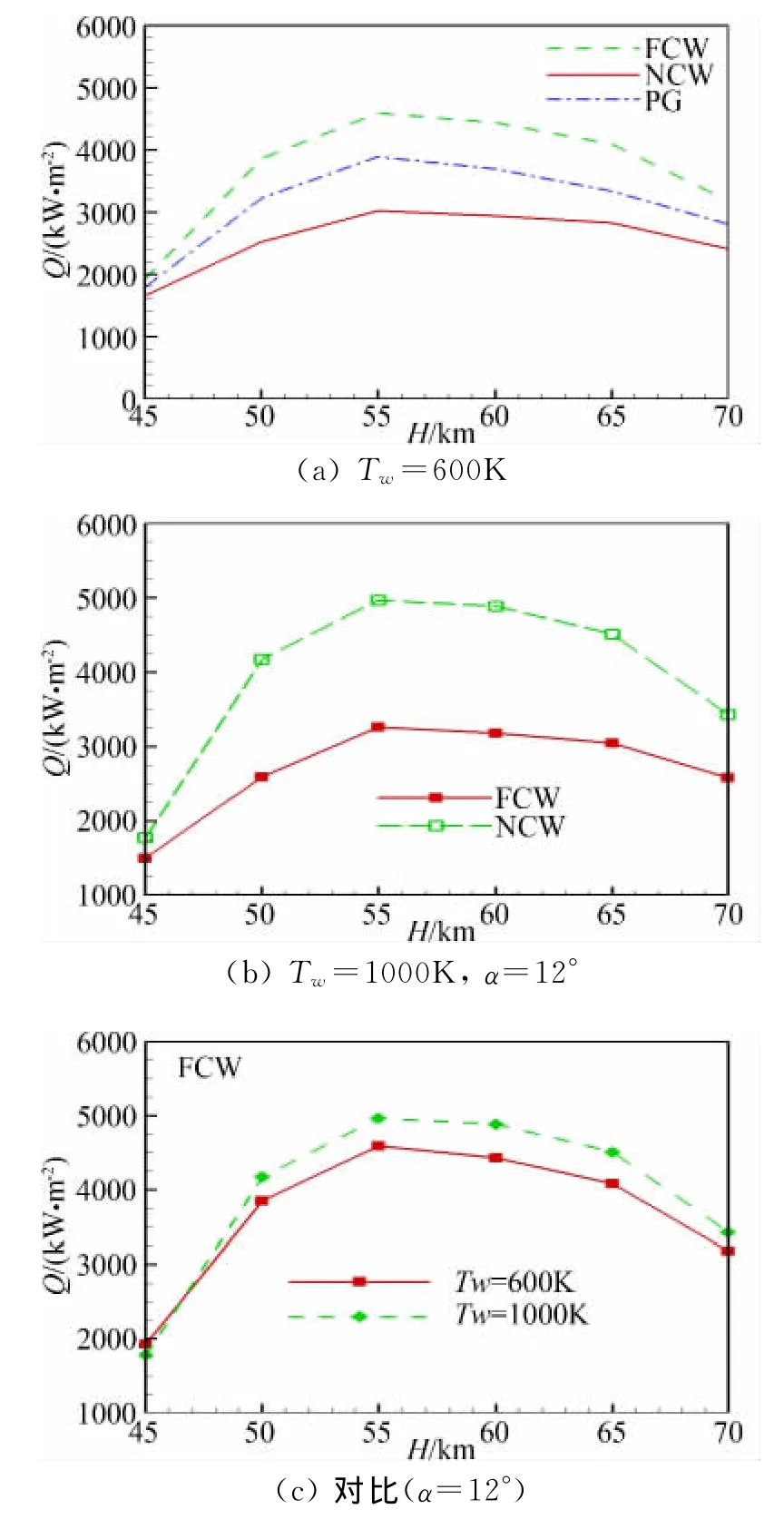
圖5 高升阻比外形駐點熱流隨飛行高度變化分布Fig.5 Variation of the heat transfer rate at the stagnational point of the high lift－to－drag hypersonic vehicle for different flight altitudes and surface temperatures

對于典型簡化高升阻比外形，頭部是RN＝35mm的半球，計算狀態：H＝45km～70km，M＝11～23，圖5給出了表面溫度Tw＝600K和Tw＝1000K時高升阻比外形駐點熱流隨飛行高度變化分布。由圖可以看出：（1）從H＝70km到H＝45km，駐點熱流最大值在H＝55km；（2）表面材料催化效應對熱流值影響較大，不同表面溫度熱流值有所不同，當表面溫度Tw＝600K時，對于完全非催化條件，駐點熱流在1650kW／m2至3000kW／m2之間，而對于完全催化條件，駐點熱流在1900kW／m2至4600kW／m2之間，當表面溫度Tw＝1000K時，對于完全非催化條件，駐點熱流在1500kW／m2至3200kW／m2之間，而對于完全催化條件，駐點熱流在1800kW／m2至5000kW／m2之間；（3）完全氣體（PG）模型計算的熱流在完全非催化和完全催化熱流之間；（4）表面溫度對熱流計算存在一定影響，表面溫度由600K上升到1000K時，H＝45km時駐點熱流略微下降，而其他高度熱流都有升高。

圖6給出了H＝55km不同表面溫度和不同飛行馬赫數高升阻比外形熱流變化分布。由圖可以看到：表面溫度變化對頭部區域的熱流影響比較明顯，當M＝10時，熱流值隨著表面溫度的增加而下降；當M＝14時，在Tw＝300K～600K時，熱流值隨著表面溫度的增加而增加，在Tw＝600K～1500K時，熱流值隨著表面溫度增加變化緩慢，且有下降趨勢；當M＝18時，在Tw＝300K～900K時，熱流值隨著表面溫度的增加而增加，在Tw＝900K～1500K時，熱流隨著表面溫度增加變化緩慢，且有下降趨勢。從分析結果看，高馬赫數和熱化學非平衡條件下，在計算氣動熱時，表面溫度最好取保守上限值，這樣就可以找到最大的駐點熱流值。

圖6 高升阻比外形不同表面溫度和飛行馬赫數條件下駐點熱流變化分布（FCW）Fig.6 Variation of the heat transfer rate at the stagnational point of the high lift－to－drag hypersonic vehicle for different flight Mach number and surface temperature

8 結束語

通過本文的研究工作，可得到如下結論：

（1）對高溫氣體效應／非平衡效應嚴重的區域，為了準確預測高超聲速飛行器氣動熱環境，我們要根據飛行環境的熱化學機制或空氣化學反應和非平衡效應的強弱，選擇適當的空氣化學反應模型和熱力學模型，不能隨意用完全氣體模型、少組分的空氣化學反應模型以及不考慮熱力學非平衡效應，特別是飛行速度非常高的情況。在本文的計算條件下，數值分析表明：（a）空氣化學反應模型7組分模型和11組分模型計算的熱流分布幾乎沒有差別，而5組分模型計算的熱流值偏小達10%以上；（b）不同熱力學模型計算的熱流分布差異較小，最大差異在10%左右，兩溫度模型計算的熱流值高于一溫度模型計算的熱流值。

（2）高馬赫數和熱化學非平衡條件下，氣動熱的數值隨著表面溫度的變化規律變得非常復雜，不能再認為氣動熱的數值遵從隨著表面溫度的升高而降低的規律；在計算氣動熱時，表面溫度最好取接近真實飛行情況分布和不同的固定值，這樣就可以找到最大的或準確的熱流值，在高超聲速飛行器的熱防護設計中更有應用價值。

本文只是分析了在再入或飛行速度在7km／s以下的條件，還需要開展系統的分析研究，如更高再入或飛行速度、不同模型尺寸和變表面溫度等情況。

［1］GNOFFO P A.Applications of program LAURA to threedimensional AOTV flowfields［R］.AIAA－86－0565.

［2］HARTUNG L C.Development of a nonequilibrium radiative heating prediction method for coupled flowfield solutions［R］.AIAA 91－1406.

［3］KEENAN J A，CANDLER G V.Simulation of graphite ablation and oxidation under re－entry conditions［R］.AIAA－94－2083.

［4］KEENAN J A，CANDLER G V.Simulation of ablation in earth atmospheric entry［R］.AIAA 93－2789，1993.

［5］曾明，杭建，林貞彬，等.不同熱化學非平衡模型對高超聲速噴管流場影響的數值分析［J］.空氣動力學學報，2008，24（3）：346－349.

［6］柳軍，劉偉，曾明，等.高超聲速三維熱化學非平衡流場的數值模擬［J］.力學學報，2003，35（6）：730－735.

［7］PEZZELLA G，VOTTA R.Finite rate chemistry effects on the high altitude aerodynamics of an apollo－shaped reentry capsule［R］.AIAA 2009－7306.

［8］VOTTA R，et al.Hypersonic low－density aerothermodynamics of orion－like exploration vehicle［J］.Journal ofSpacecraftandRockets，2009，46（4）：781－787.

［9］董維中.熱化學非平衡效應對高超聲速流動影響的數值計算與分析［D］.［博士學位論文］.北京航空航天大學，1996.

［10］董維中.氣體模型對高超聲速再入鈍體氣動參數計算影響的研究［J］.空氣動力學學報，2001，19（2）：197－202.

［11］NETTERFIELD M P.Validation of a Navier－Stokes code for thermochemical nonequilibrium flows［R］.AIAA 92－2878.

［12］MUYLAERT J，et al.Standard model testing in the European high facility F4and extrapolation to flight［R］.AIAA－92－3905.

［13］CANDER G V，MACCORMACK R W.The computation of hypersonic ionized flows in chemical and thermal nonequilibium［R］.AIAA－88－0511.

［14］董維中，高鐵鎖，丁明松.高超聲速非平衡流場多個振動溫度模型的數值研究［J］.空氣動力學學報，2007，25（1）：1－6.

［15］董維中，高鐵鎖，張志成.再入體實驗模型熱化學非平衡繞流流場的數值分析［J］.空氣動力學學報，2008，26（2）：163－166.

［16］董維中，樂嘉陵，劉偉雄.駐點壁面催化速率常數確定的研究［J］.流體力學實驗與測量，2000，14（3）：1－6.

［17］董維中，樂嘉陵，高鐵鎖.鈍體標模高焓風洞試驗和飛行試驗相關性的數值分析［J］.流體力學實驗與測量，2002，16（2）：1－8.