大跨橋梁抖振力與脈動風速空間相關性的對比研究

李少鵬，李明水，馬存明，廖海黎

（西南交通大學 風工程試驗研究中心，四川 成都 610031）

0 引 言

大跨度橋梁可以視為一種細長結構，傳統的抖振分析一般基于片條假設，近似認為脈動風及其引起的非定常氣動力具有線性關系，即抖振力的空間相關性與脈動風的空間相關性是等價的［1］。研究結果表明，對于大跨橋梁，脈動風的順風向積分尺度（大約100m～200m）至少10倍于結構的特征尺寸，因此紊流引起的非定常阻力可以采用片條假設較為精確的描述。而脈動風的豎向積分尺度（大約30m～50m）與橋寬接近，因而抖振升力與抖振力矩的跨向分布則不能用片條假設精確描述［2］，這也是橋梁抖振精細化研究的一個重要方向。

Roberts認為在風洞中由格柵產生的紊流是各項同性的，其脈動風譜可以用Von Karman譜良好的擬合，并據此提出了適用于各向同性紊流的空間相關性計算方法［3］。Mann等人也提出了類似的、計算各向同性紊流空間相關性的計算公式［4－6］。李等［7］基于經典空氣動力學理論進一步研究了各向同性紊流下抖振力的空間相關性，定義了抖振力和脈動風空間交叉譜以及無量綱相干函數的一般表達式，并通過實際算例驗證了其理論的有效性。Larose［8－9］和馬［10］運用尖塔、格柵形成紊流場，通過節段模型測壓試驗，直接測得表面壓力分布，將測點壓力沿斷面積分即可得到該截面的抖振力，進而研究抖振力的跨向相關性，試驗表明，對于箱形斷面，抖振力的跨向相關性大于脈動風的相關性。

在Larose等人的節段模型測壓試驗中，由于風洞試驗段尺寸以及模型縮尺比的限制，故采用的試驗段長度較小，其中，Larose節段模型試驗段長度0.3m，馬［10］的試驗段長度0.48m，因此以上試驗均無法反映較長跨向間距內抖振力的跨向相關性。而且以上試驗成果均反映的是風洞被動模擬紊流場下抖振力的跨向相關性，而風洞試驗結果能否反映自然大氣紊流下抖振力的跨向相關性尚無定論。為了突破上述試驗瓶頸，進一步研究抖振力的跨向分布規律，理論分析方法可成為解決這一難題的有效手段之一。

本文將以抖振升力為例，通過理論分析手段，建立能夠合理描述抖振力跨向相關性的數學模型，并與Larose的試驗結果進行對比，進而得到抖振力跨向相關性的一般規律。本文的研究成果可以推廣到抖振力矩與阻力的跨向相關性研究之中。

1 抖振力跨向相關性數學模型

基于各向同性紊流假設，以升力為例，抖振力及脈動風的跨向相關性以互相關系數來表示：

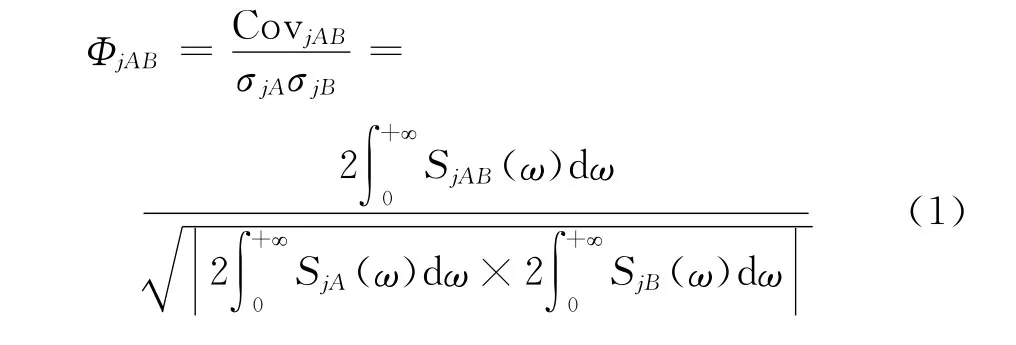
式中，ΦjAB為A、B兩點的互相關系數（j＝1表示抖振升力，j＝2表示縱向脈動分量，j＝3表示豎向脈動分量）；CovjAB為A、B兩點的協方差；σjA、σjB分別為A或B點的均方根；SjAB為A、B兩點的互譜；SjA、SjB分別為A、B點的點譜。

對于各向同性紊流，可以認為σjA＝σjB，即SjA＝SjB（j＝1～3），因此下文用Sj來表示任意兩點的點譜。由此式（1）可以化簡為如下形式：

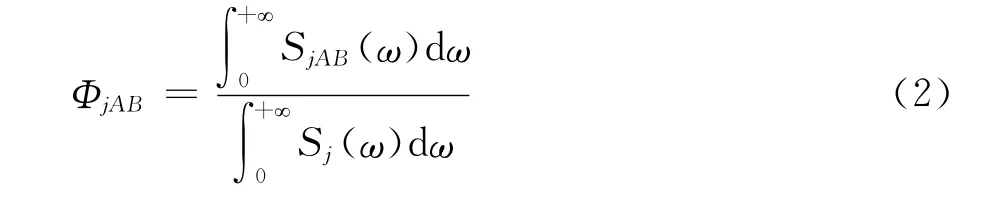
式中，j＝1～3，意義同上。

Larose定義如下形式的抖振升力模型：

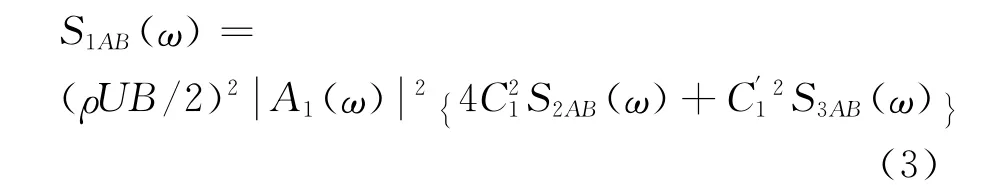
式中，S1AB、S2AB及S3AB的定義與式（1）相同；A1為氣動導納函數；C1為升力系數；表示升力系數導數。

式（2）中氣動導納采用Sears函數形式的Liepmann［11］近似表達式：

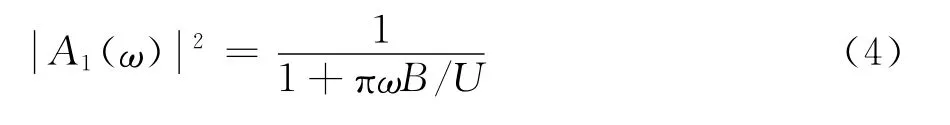
式中，B為橋寬，U為平均風速。

本文采用李等［4］提出的脈動風互譜計算公式：

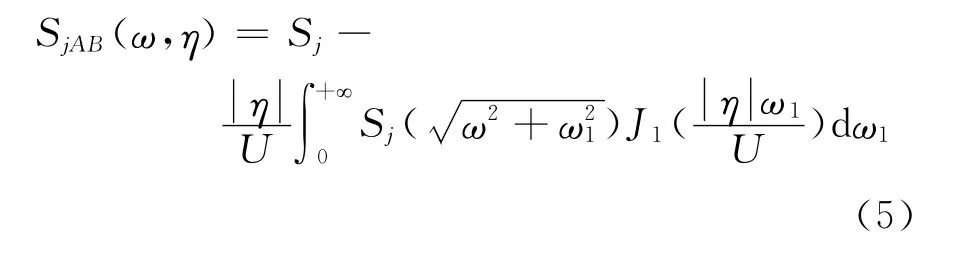
式中，j＝2或3，分別表示縱向及豎向脈動分量；η為A、B兩點距離；U為主梁水平高度處的平均風速；J1（ω）為第一類Bessel函數。

在此，以Von Karman譜表示風洞模擬風譜，以基于大量實測而建立的自然大氣功率譜Simiu譜［12］和Panofsky譜［13］分別表示縱向、豎向自然大氣風譜，根據式（2）～式（5），分別對兩類風譜下抖振力及脈動風沿跨向的互相關系數進行數值積分，由此可得其精確解。

Von Karman譜［14］如下表示：

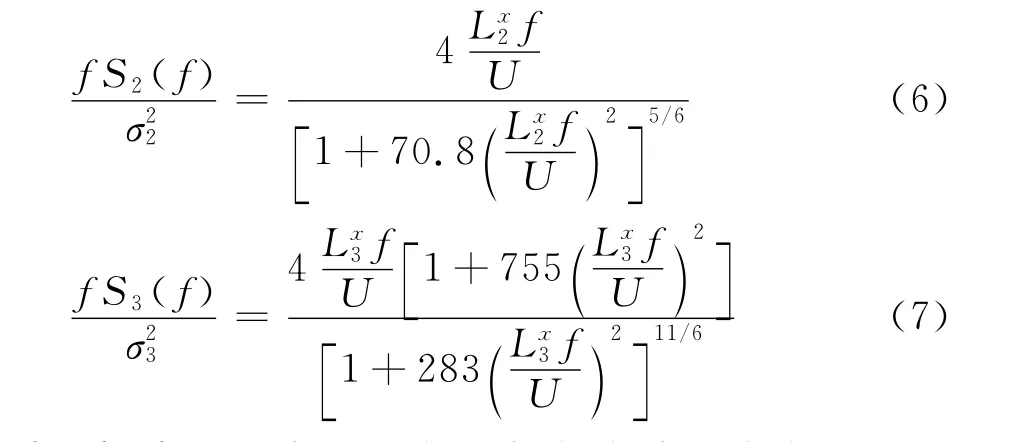
式中，、分別表示縱向及豎向脈動風均方值；、分別為縱向和豎向脈動風積分尺度。

對于各向同性紊流，一般認為：＝以及＝／2，但 Bearman［15］發現風洞試驗產生的各向同性紊流滿足＝1.46，因而豎向 Von Karman譜可以表示為：

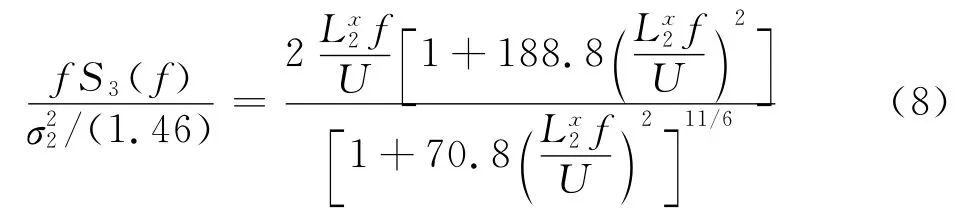
Simiu譜如下表示：

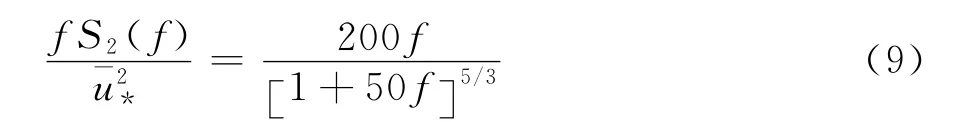
式中，f＝nz／U；為剪切速度均方值。

Panofsky譜如下表示：

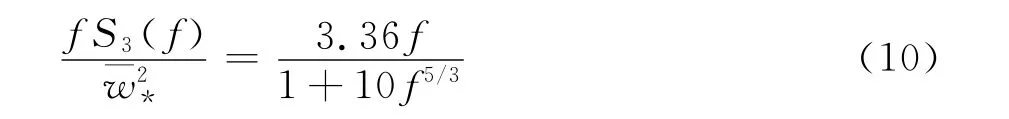
式中，f＝nz／U為剪切速度均方值，對于各向同性紊流，可近似認為≈。

將式（6）～式（10）代入式（2）～式（5），可得抖振力及脈動風沿跨向互相關系數的一般性表達式：

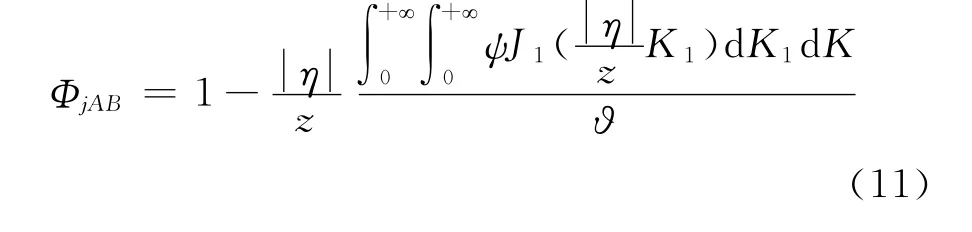
式中，j＝1～3；ψ、?為待定參數；K＝為無量綱折減頻率（對于自然大氣風譜，z表示高度；對于風洞模擬風譜，z表示縱向積分尺度Lu）。

對于不同類型的風譜，只需改變參數ψ、?即可得到抖振力以及脈動風沿跨向的互相關系數，在風洞模擬風譜以及自然大氣風譜下，ψ、?的取值分別如下：

對于縱向Von Karman譜：

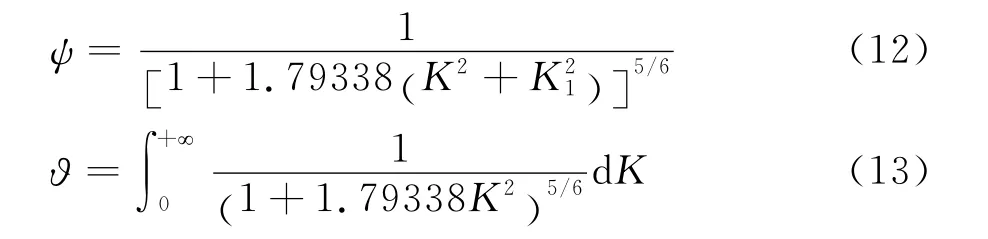
對于豎向Von Karman譜：

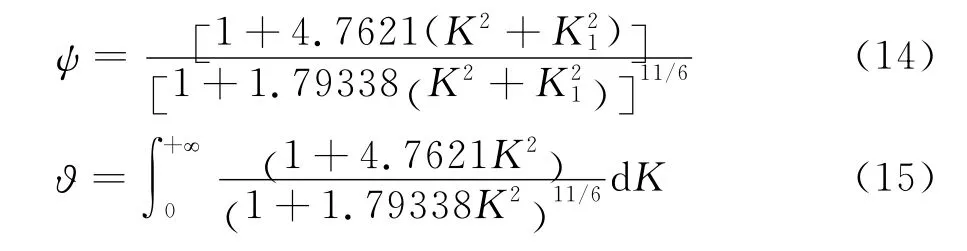
基于風洞試驗風譜的抖振力：

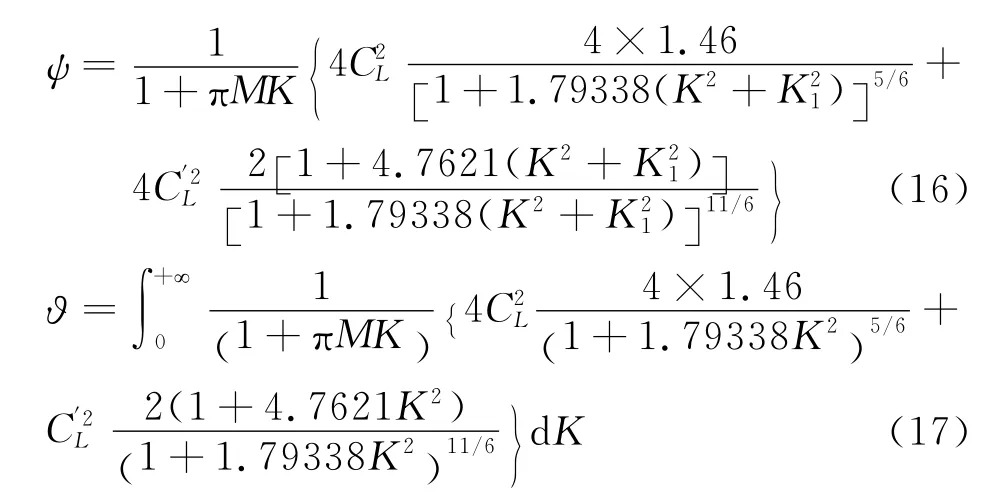
式中，M＝B／z；z為主梁水平高度。

對于Simiu譜：

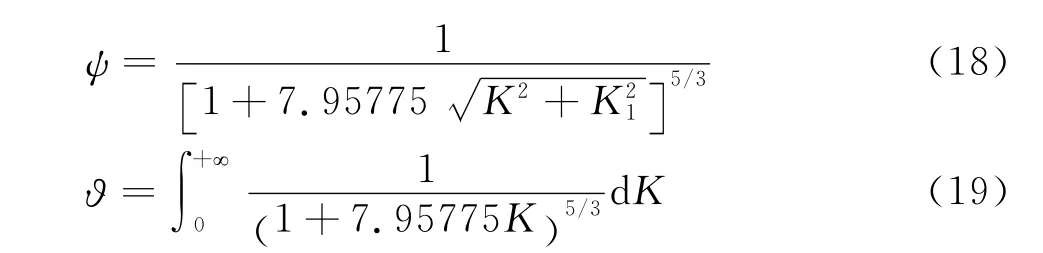
對于Panofsky譜：

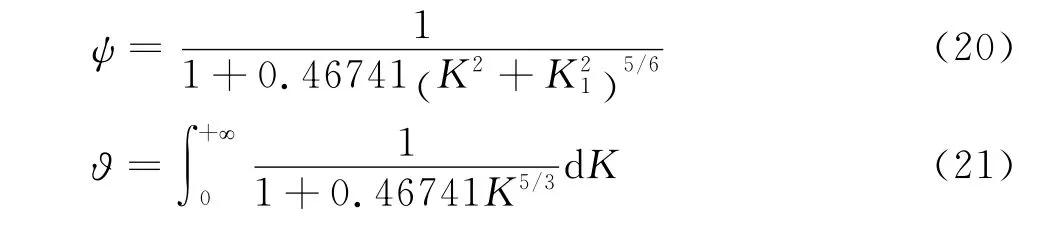
基于自然大氣風譜的抖振力：

不同的跨向間距內，在風洞模擬風譜下抖振力及脈動風的跨向相關系數分別如圖1、圖2所示，為了清晰表示，圖2橫坐標采用對數坐標。

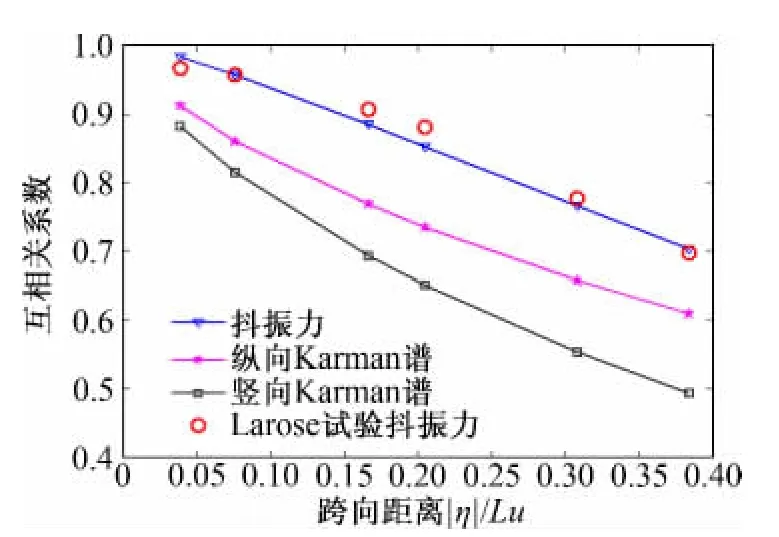
圖1 風洞模擬風譜下抖振力及脈動風的互相關系數Fig.1 Cross－correlation coefficient of buffeting force ＆turbulence based on tunnel wind spectrum

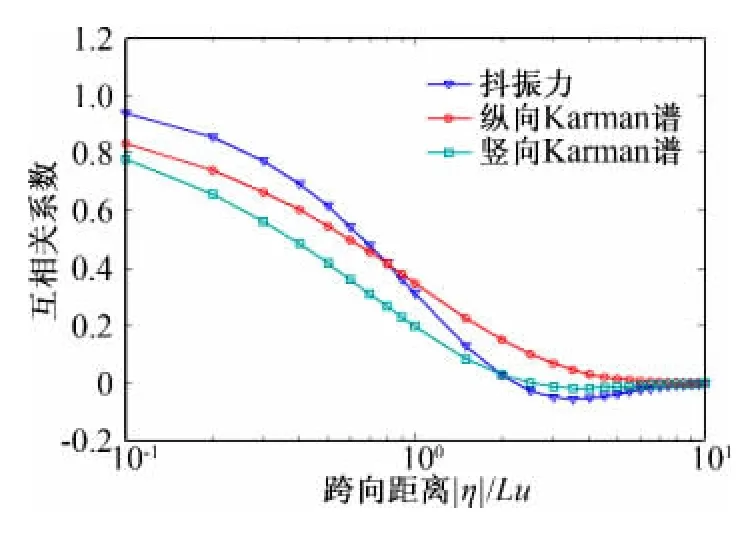
圖2 風洞模擬風譜下抖振力及脈動風的互相關系數Fig.2 Cross－correlation coefficient of buffeting force ＆turbulence based on tunnel wind spectrum

自然大氣風譜下抖振力與脈動風的跨向相關系數如圖3所示：

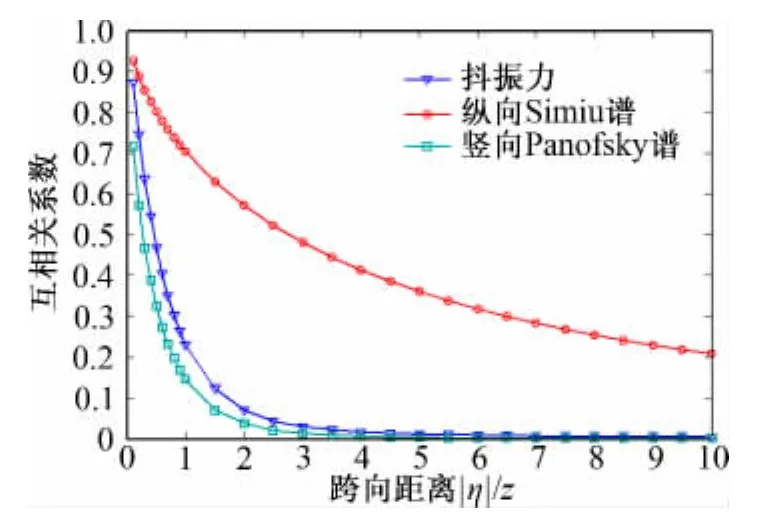
圖3 自然大氣風譜下抖振力與脈動風互相關系數Fig.3 Cross－correlation coefficient of buffeting force ＆turbulence based on natural wind spectrum

綜合圖1～圖2結果可以得出，在風洞模擬風譜下，抖振力的跨向相關性高于脈動風的相關性這一結論僅在一定的跨向間距內成立。由圖1所示，在較小間距內，理論計算得到的抖振力互相關系數與Larose的風洞試驗結果很好的吻合。但是，如圖2所示，隨著跨向距離的增大，抖振力的跨向相關性逐漸低于脈動風的跨向相關性，并介于縱向與豎向脈動風的相關性之間。而在自然大氣風譜下，由圖3可以清晰的反映出抖振力的跨向相關性介于縱向脈動風與豎向脈動風的相關性之間。

由此，可以大膽推斷，抖振力的跨向相關性高于脈動風的相關性這一論斷成立是有一定限定條件的，即在風洞試驗產生的紊流場中，其僅在一定的跨向間距內成立；而在自然大氣紊流場中，抖振力的跨向相關性則介于縱向脈動分量與豎向脈動分量的相關性之間。

2 基于Davenport相干函數經驗公式的抖振力跨向相關性

由于自然大氣中的脈動風不符合各向同性紊流假設，為了進一步驗證上述推斷的有效性，下面采用Davenport提出的相干函數經驗公式來求解自然大氣風譜下抖振力的跨向相關性。

Roberts［3］和 Houblt［16］都曾定義過如下形式的空間譜的相關系數函數：

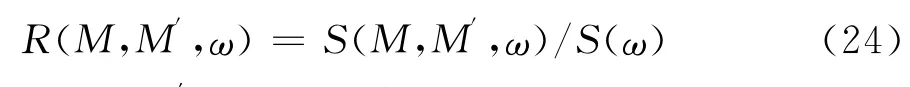
式中，M和M′為空間任意兩點。

按照上述定義，本文采用下式來計算兩點脈動風的互譜：

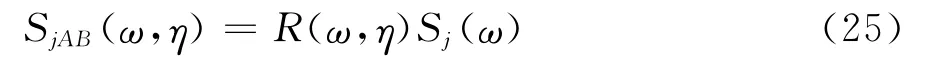
式中，j＝2～3，分別表示縱向及豎向脈動分量；R（ω，η）為相干函數，這里采用Davenport［17］相干函數經驗公式：

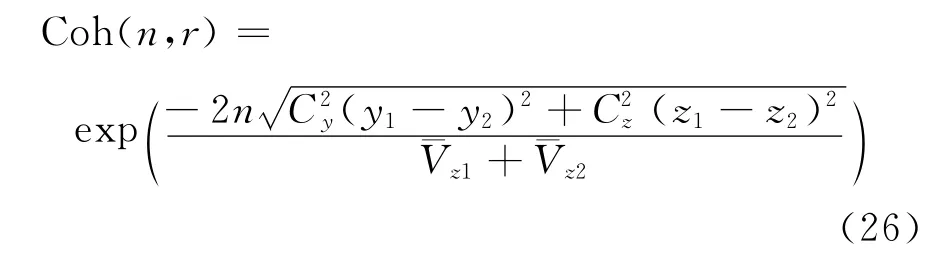
式中，n為頻率；r為空間兩點距離；y1、y2、z1、z2分別為空間兩點的橫向坐標和豎向坐標；1、2分別為高度z＝z1和z＝z2處的平均風速；Cy、Cz分別為與橫向及豎向相關的指數衰減系數，Cy和Cz一般可取Cy＝8，Cz＝7。

考慮到橋梁主梁的高度較小，近似地認為整個主梁在同一水平高度上，即z1＝z2；則式（26）可以化簡如下：

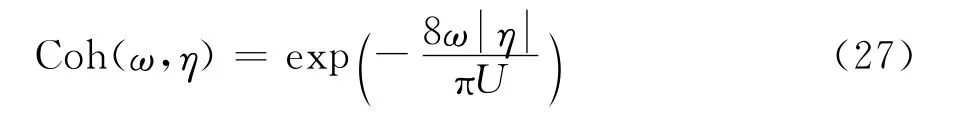
式中，η為跨向距離，U為主梁水平高度處平均風速。

將式（27）代入式（25）即可得到空間兩點抖振力及脈動風的互譜：

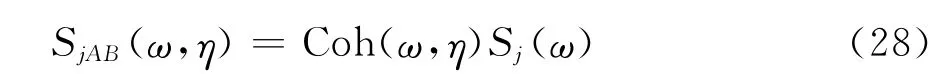
將自然大氣風譜及式（28）代入式（2）即可得到此風譜下的抖振力和脈動風的跨向互相關系數，分析結果如下所示：

對于Simiu譜：

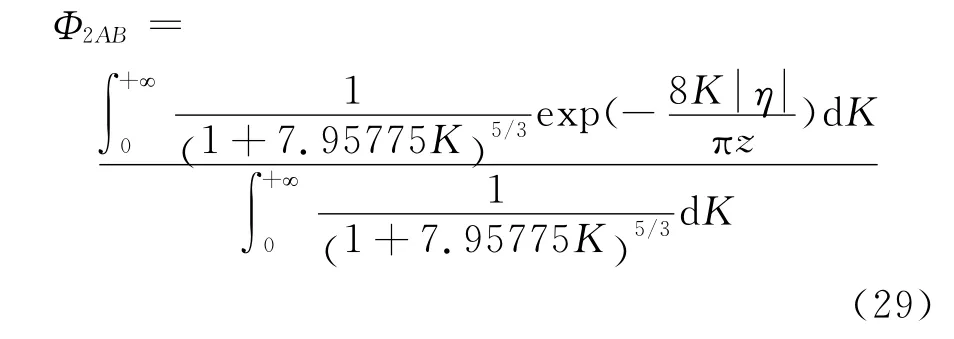
對于Panofsky譜：

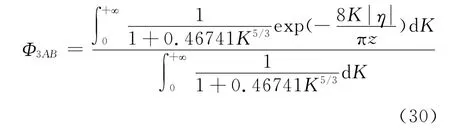
基于自然大氣風譜的抖振力參數如下所示：

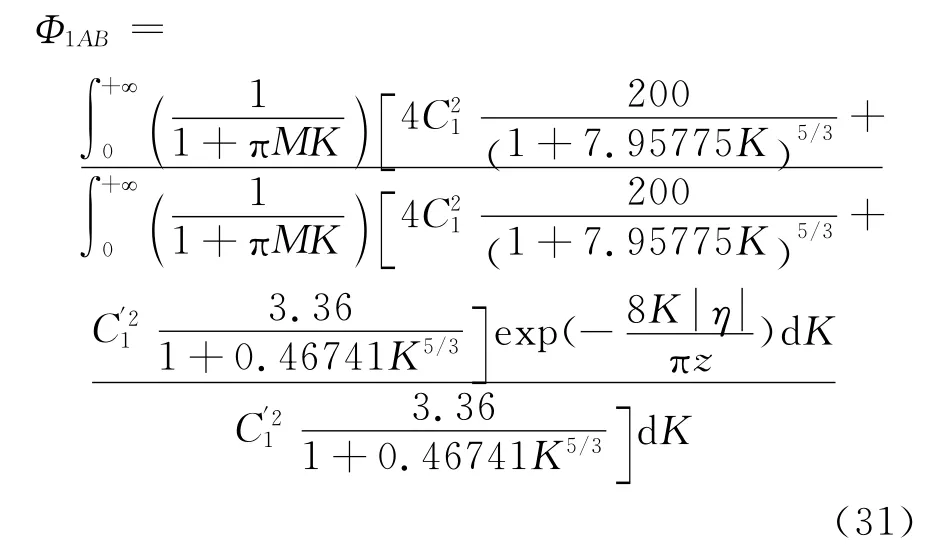
由式（29）～式（31）可得自然大氣風譜下抖振力及脈動風的跨向互相關系數如下所示。

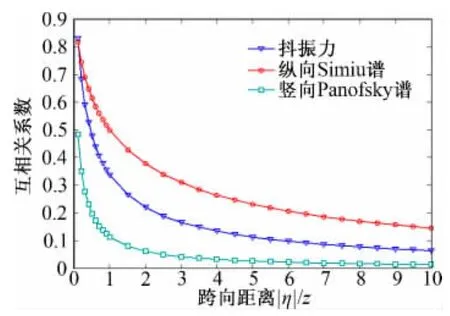
圖4 基于經驗相干函數的抖振力及脈動風互相關系數Fig.4 Cross－correlation coefficient of buffeting force ＆turbulence based on empirical coherence function

對比圖3、圖4可以發現，根據Davenport相干函數經驗公式得到的抖振力及脈動風的互相關系數與第2節理論計算結果趨勢一致，由此可以驗證在自然大氣紊流場中本模型的有效性。

3 結 論

本文通過理論分析方法，深入研究了抖振力與脈動風在不同流場以及較大跨向間距范圍內的跨向相關性，由此可以得以下結論：

（1）在風洞模擬紊流場中，在較小的跨向間距內，抖振力的跨向相關性高于脈動風的相關性，并與Larose試驗結果吻合，而隨著跨向間距的增大，抖振力的跨向相關性逐漸低于脈動風的相關性。

（2）在自然大氣紊流場中，抖振力的跨向相關性介于縱向脈動風與豎向脈動風的相關性之間。

［1］DAVENPORT A G.The application of statistical concepts to the loading of structures［J］.ICEProceedings，1961，19（4）：449－472.

［2］LAROSE G L.The spatial distribution of unsteady loading due to gusts on bridge decks［J］.JournalofWindEngineeringandIndustrialAerodynamics，2003：1431－1443.

［3］ROBERTS J B，SURRY D.Coherence of grid generated Turbulence［J］.JournalofEngineeringMechanics，ASCE，1973，99（6）：1227－1245.

［4］MANN J.The spatial structure of neural atmospheric surface－layer turbulence［J］.JournalofFluidMechanics，1994，273：141－168.

［5］MANN J，KRISTENSEN L，COURTNEY M S.The great belt coherence experiment－a study of atmospheric turbulence over water［R］.Riso Report R－596，1991：51.

［6］FORSCHING H W.氣動彈性力學原理［M］.沈克揚，譯.上海科技出版社，1981：695－696.

［7］李明水，賀德馨，王衛華.大跨度橋梁抖振響應的頻域分析［J］.空氣動力學學報，2000，18（1）：74－80.

［8］LAROSE G L，TANAKA H，GIMSING N J，et al.Direct measurement of buffeting wind forces on bridge decks［J］.JournalofWindEngineeringandIndustrialAerodynamics，1998，74－76：809－818.

［9］LAROSE G L.Gust loading on streamlined bridge decks［J］.JournalofFluidandStructures，1998，12（5）：511－536.

［10］馬存明.流線箱型橋梁斷面三維氣動導納研究［D］.［博士論文］.西南交通大學，2007.

［11］LIEPMANN H.On the application of statistical concepts to buffeting problem［J］.JournalofAeronautical Science，1952，19（12）：793－800.

［12］SIMIU E.Wind spectra and dynamic alongwind response［J］.JournaloftheStructuralDivision，1974，100：1897－1910.

［13］BUSH N E，PANOFSKY H A，Recent spectra of atmospheric turbulence［J］.TheQuarterlyJournaloftheRoyal MeteorologicalSociety，1968，94（400）：132－148.

［14］SHIAU B S.Velocity spectra and turbulence statistics at the northeastern coast of Taiwan under high－wind conditions［J］.JournalofWindEngineeringandIndustrialAerodynamics，2000，88（2）：139－151.

［15］BEARMAN P W.Some measurements of the distortion of turbulence approaching a two－dimensional bluff body［J］.JournalofFluidMechanics，1972，53（3）：451－467.

［16］HOUBLT J G.On the response of structural having multiple random inputs［R］.WGLR－Jahrbuch 1957，1958.

［17］DAVENPORT A G.The dependence of wind load upon meteorological parameters［A］.Proceedings of the international research seminar on wind effects on building and structures［C］.University of Toronto Press，1968：19－82.