基于免疫遺傳算法的發動機懸置系統優化與魯棒性分析

李彥保，李友真，張 旭，王桂龍，沈 勇

Li Yanbao1，Li Youzhen2，Zhang Xu3，Wang Guilong2，Shen Yong3

（1. 合肥工業大學交通運輸工程學院，安徽 合肥 230009；2. 合肥工業大學機械與汽車工程學院，安徽 合肥 230009；3. 上海汽車集團股份有限公司技術中心，上海 201804）

0 引 言

發動機是引起汽車振動的主要原因之一，對汽車舒適性和 NVH（Noise,Vibration,Harshness）特性影響較大。一方面，駕乘人員對汽車舒適性要求越來越高，另一方面，輕量化技術的迅猛發展，發動機對整車振動的影響更為顯著，而發動機懸置系統能夠減弱發動機、路面與輪胎所引起的振動，因而建立正確的模型并選擇合理的參數成為實現系統優化的關鍵[1]。

發動機懸置系統的模型比較復雜，過度依賴梯度信息的傳統優化方法并不適用；遺傳算法雖不需要梯度信息，但搜索到的結果比較極端[2]。文中用魯棒性優化設計與解耦優化設計相結合的思想對發動機懸置系統進行了優化設計與分析，首先建立發動機懸置系統的數學模型；然后運用遺傳算法和免疫算法相結合的方法對某型客車發動機的懸置剛度參數進行優化；最后利用蒙特卡羅（Monte Carlo）法對懸置系統進行魯棒性分析。

1 數學模型的建立

發動機懸置系統是一個復雜的 6自由度振動系統，為了簡化運算，根據研究目的做以下假設：動力總成和車架作為剛體；橡膠元件的彈性是線性的，阻尼忽略不計。根據以上假設建立 6自由度系統模型[3]，如圖1所示。

其中，o為動力總成質心，x軸指向發動機前端，z軸垂直地面向上，y軸由右手定則確定；懸置點 1、2、3、4平置于發動機的兩側；u、v、s為懸置系統的3條彈性主軸方向。

由此可得懸置系統的廣義坐標為：q={x，y，z，θx，θy，θz}。系統的動態特性動力學方程為：

其中，M為系統質量矩陣；C為系統阻尼矩陣；K為系統剛度矩陣；q為廣義坐標；F(t) 為系統所受激振力。

采用 6自由度無阻尼自由振動系統，故可將式（1）寫為：

由式（2）可求解出懸置系統的固有頻率ωj(j=1,2, 3, 4, 5, 6)和固有振型φ。

2 系統振動特性分析

文中研究的是 6自由度懸置系統，要求其固有頻率分布合理，否則在某些工況下可能會使系統產生多自由度耦合振動。在實際應用中，多自由度系統中產生耦合是無法消除的，所以目的是將耦合降到最低，即提高系統解耦率。運用能量解耦法[4]，即從能量的角度對懸置系統各自由度耦合進行分析，并可得出各自由度方向上的解耦程度，從而為優化提供依據。

當系統以第j階模態振動時，定義能量分布矩陣E(k,l)為

其中，φ(k,j)、φ(l,j)為第j階振型第k、l個元素；M(k,l)為質量矩陣的第k行l列元素；ωj為第j階固有頻率；k,l,j=1, 2, 3, 4, 5, 6。

當系統以第j階模態振動時，第k個廣義坐標分配能量占系統總能量的百分比為

Qa(j,k)代表解耦程度的高低，其值越大越好。若Qa(j,k)=100%，說明第j階模態振動完全解耦。

3 模型的優化方法

3.1 免疫遺傳算法

免疫遺傳算法是綜合免疫算法和遺傳算法提出的一種新的復合算法[5-6]，從而彌補了2種算法固有的不足，又能使各自的優點充分發揮。運用免疫遺傳算法對發動機懸置系統各自由度方向上解耦程度進行分析，進而得到最優解，實現較高程度的解耦。免疫遺傳算法流程如圖2所示。

3.2 目標函數

將動力總成懸置系統的 6自由度能量解耦最大作為優化設計的目標，因此系統能量解耦目標函數可確定為：

式中，αi為對應于第i階頻率的加權因子；Qi為各自由度能量百分比。

3.3 設計變量

考慮到動力總成本身的物理參數不易改變，安裝位置的限制以及制造成本的約束，因此選取懸置元件的主剛度值K=(k1,k2,……kn)（n為懸置剛度個數）為設計變量。

3.4 約束條件

對動力總成懸置系統參數進行優化時，主要從兩個方面對其添加約束：

（2）要求其主軸剛度應滿足：kimin≤ki≤kimax(i=1, 2, …n) 。

4 實例的優化與分析

4.1 懸置系統的優化

針對某特定款型客車進行懸置系統的實例優化與分析。其動力總成懸置系統布置情況為：6缸 4沖程式發動機，4點支撐平置式對稱分布。

初始條件給出懸置點坐標、總成參數及各主剛度值，由此可以根據前述公式計算出懸置系統的固有頻率及能量分布。分別如表1～表3所示。

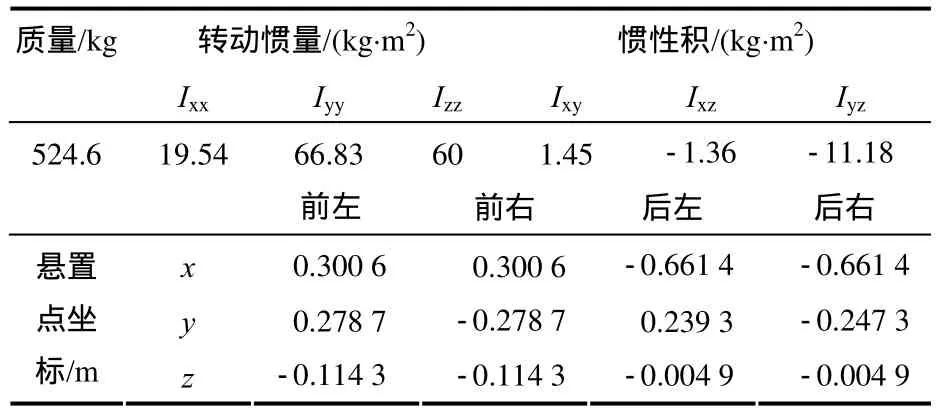
表1 懸置點坐標及系統參數

表2 系統各懸置點主剛度值

表3 懸置系統固有頻率和能量分布

從表3能量分布矩陣中可以看到，在6個自由度方向上的解耦率分別是 79.48%、88.81%、51.37%、67.60%、58.3%、62.07%，均在 90%以下，解耦率明顯偏低，故需對其進行優化，提高解耦率，從而削弱各自由度之間的耦合振動。

4.2 系統的優化結果

運用文中提出的免疫遺傳算法對該懸置系統的主剛度值進行優化，并在Matlab軟件平臺下進行編程，實現優化過程的求解計算，從而得到系統主剛度值的最優解，進而求得系統的固有頻率和能量分布。如表4、表5所示。

表4 優化后各懸置點主剛度值

表4和表5中的數據均滿足優化設計所提出的約束條件，所以可取。另外，表 5顯示優化后系統在6個自由度方向上的解耦率均大于90%，這說明系統得到了較高程度的解耦。

表5 優化后系統固有頻率和能量分布

4.3 魯棒性分析

蒙特卡羅法是一種計算機模擬方法，又稱統計模擬法，是以概率統計理論為指導的一類數值計算方法[7]。在實際使用過程中，懸置系統的各向主剛度值基本在（-12%，+12%）范圍內波動，即應用過程與理論設計存在差異。所以在實際應用中需要了解主剛度值的變化對系統解耦程度的影響。

采用蒙特卡羅法分別對優化前和優化后的結果進行魯棒性分析，分別基于目標函數建立響應面模型，經過2000次隨機試驗分析，結果如圖3、圖4所示。

將以上分析結果進行正態分布擬合，優化前：Q1～N（0.8704，0.3788）；優化后：Q2～N（0.0235，0.0276）。可以看到，經過免疫遺傳算法優化后目標函數均值從0.8704減小為0.0235，優化效果較為顯著。

現以單自由度解耦率為目標函數分別建立 6個自由度方向上的響應面模型，并運用蒙特卡羅法對其進行分析，結果如圖5所示。

由圖 5可計算出各自由度方向上的標準差分別為：0.45%、1.32%、2.36%、0.56%、1.78%、0.86%，表明各自由度均有很高的魯棒性。

通過運用蒙特卡羅法分別對基于 6自由度和單自由度建立的響應面模型進行分析，表明優化后的發動機懸置系統具有較高的魯棒性。

5 結束語

依據能量解耦法，運用免疫遺傳法對發動機懸置系統進行優化，實現使系統固有頻率在合理區域內，且主軸剛度滿足要求，提高系統解耦程度，達到優化的目的；同時，采用蒙特卡羅法也證明了懸置系統經優化后具有較高的魯棒性，具有較好的指導意義和工程價值。

[1]上官文斌，蔣學鋒．發動機懸置系統的優化設計[J]．汽車工程，1992，14（2）：41-48．

[2]Sorge F．A Simple Model for the Axial Thrust in V-Belt Daves[J]．Journal of Mechanical Design，1996，l18：589-591．

[3]黃信，柏世川，章竹一．汽車發動機懸置系統設計[J]．合肥工業大學學報（自然科學版），2009，32（Z1）：125-127．

[4]呂兆平．能量法解耦在動力總成懸置系統優化設計中的運用[J]．汽車工程，2008，30（6）：523-526．

[5]王煦法，張顯俊，曹先彬，等．一種基于免疫原理的遺傳算法[J]．小型微型計算機系統，1999，20（2）：117-120．

[6]TamboliJ A，Joshi S G Optimum Design of a Passive Suspension System of a Vehicle Subjected to Actual Random Road Excitations[J]．Journal of Soundand Vibration，1999，219（2）：193-205．

[7]張蕾，董恩國，申焱華. 基于蒙特卡羅法的氣門彈簧穩健設計研究[J]. 機械科學與技術，2008，27（8）：1066–1069．