基于數(shù)據(jù)的MATLAB系統(tǒng)辨識工具箱模型識別

陳嵐峰，張亞琴，程立英，張志美

（1.沈陽師范大學(xué) 物理科學(xué)與技術(shù)學(xué)院，沈陽 110034；2.沈陽師范大學(xué) 實驗教學(xué)中心，沈陽 110034）

0 引 言

利用控制理論去解決實際問題時，首先需要建立被控對象的數(shù)學(xué)模型［1］。現(xiàn)代復(fù)雜工程系統(tǒng)越來越趨近于多元化、模塊化［2］，實際工程中存在著大量控制對象要建立用于描述其行為特性的數(shù)學(xué)模型，系統(tǒng)辨識是根據(jù)系統(tǒng)的輸入輸出時間函數(shù)來確定描述系統(tǒng)行為的數(shù)學(xué)模型，是現(xiàn)代控制理論中的一個分支。隨著各門科學(xué)的定量化，系統(tǒng)辨識的應(yīng)用越來越廣泛，不僅是航空、航天、電力、化工等工程應(yīng)用領(lǐng)域，還延伸到生物信息科學(xué)、醫(yī)學(xué)工程、社會經(jīng)濟等各學(xué)科［3］。

1 系統(tǒng)辨識基本理論

系統(tǒng)辨識是在對輸入和輸出觀測的基礎(chǔ)上，在指定的一類系統(tǒng)中，確定一個與被識別的系統(tǒng)等價的系統(tǒng)［4］。系統(tǒng)辨識理論是通過考察輸入輸出數(shù)據(jù)來建立動態(tài)系統(tǒng)模型的科學(xué)技術(shù)，是聯(lián)系控制理論和數(shù)學(xué)模型的抽象世界與實際應(yīng)用的現(xiàn)實世界的接口［5］。對系統(tǒng)進行分析的主要問題是根據(jù)輸入時間函數(shù)和系統(tǒng)的特性來確定輸出信號。對系統(tǒng)進行控制的主要問題是根據(jù)系統(tǒng)的特性設(shè)計控制輸入，使輸出滿足預(yù)先規(guī)定的要求。

2 系統(tǒng)辨識方法

辨識的實質(zhì)就是從一組模型類中選擇一個模型，按照某種準則，使之能最好地擬合所關(guān)心的實際過程的靜態(tài)或動態(tài)特性。常用的系統(tǒng)辨識方法有最小二乘法和輔助變量法。

2.1 最小二乘法

首先給出模型類型，在該類型下確定系統(tǒng)模型的最優(yōu)參數(shù)。這種具有格式規(guī)范的辨識方法可以演繹成遞推形式。遞推的最小二乘算法計算量小，可以用于在線辨識，即使辨識對象隨時間發(fā)生變化，模型也可以對其進行跟蹤，不斷地進行更新和修正辨識參數(shù)，從而成為一種被廣泛采用的辨識方法。

應(yīng)用最小二乘法對系統(tǒng)模型參數(shù)進行辨識的方法有離線辨識和在線辨識兩種［6］。離線辨識是在采集到所需全部輸入輸出數(shù)據(jù)后，用最小二乘法對數(shù)據(jù)集中處理，從而獲得模型參數(shù)的估計值；而在線辨識是一種在系統(tǒng)運行過程中進行的遞推的辨識方法，所應(yīng)用的是實時采集的系統(tǒng)輸入輸出數(shù)據(jù)，應(yīng)用遞推算法對參數(shù)估計值進行不斷修正，以取得更為準確的參數(shù)估計值。

2.2 輔助變量法

由于最小二乘估計是非一致的、有偏差的，為了克服它的缺點，形成了一些以最小二乘法為基礎(chǔ)的辨識方法：廣義最小二乘法（GLS）、輔助變量法（IVA）和增廣矩陣法（EM），以及將一般的最小二乘法與其他方法相結(jié)合的方法［7］。輔助變量法是很有使用價值的辨識方法，尤其當噪聲是有色的，而噪聲的模型結(jié)構(gòu)又不好確定時，輔助變量法更能顯示出它的優(yōu)勢［8］。

輔助模型辨識思想（auxiliary model identification idea）是借助于系統(tǒng)的可測信息，建立一個輔助模型，用輔助模型的輸出代替系統(tǒng)的不可測變量的一種辨識方法［9］。它的基本思想是在辨識過程中設(shè)法構(gòu)造一種新的變量信號，稱這個信號變量為輔助變量。這個輔助變量的特點是它與過程誤差是不相關(guān)的，但與過程中的有用信號則是相關(guān)的。利用這個相關(guān)法的思想，可以估計出模型的參數(shù)［10］。

3 系統(tǒng)辨識工具箱的簡介

Matlab的系統(tǒng)辨識工具箱提供了進行系統(tǒng)辨識的有力工具［11］。系統(tǒng)辨識中的模型是考慮了噪聲影響的隨機模型［12］。MATLAB工具箱包括模型類和模型結(jié)構(gòu)參數(shù)的確定兩部分內(nèi)容。利用MATLAB編程環(huán)境，開發(fā)圖形界面和多種辨識模型與算法等［13］。模型類的確定主要是根據(jù)先驗知識對過程的特性進行一定程度的假設(shè)，明確所要建立的模型是靜態(tài)的還是動態(tài)的，是連續(xù)的還是離散的、是線性的還是非線性的、是參數(shù)模型還是非參數(shù)模型。支持的模型類主要有：非參數(shù)模型類中的脈沖響應(yīng)模型；參數(shù)模型中的（ARX）模型、（ARMAX）模型、Box－Jenkins模型和狀態(tài)空間模型等。在模型結(jié)構(gòu)確定以后，就可以進行模型參數(shù)的辨識了，MATLAB中對模型進行參數(shù)辨識方法包括最小二乘法、誤差預(yù)報估計法、輔助變量法、幾何網(wǎng)絡(luò)法等。基于最小二乘法［14］，在MATLAB仿真環(huán)境下，待辨識模型的輸入輸出數(shù)據(jù)的導(dǎo)入如圖1所示。

圖1 數(shù)據(jù)的導(dǎo)入

工具箱中提供交互式的圖形界面工具，能方便實現(xiàn)數(shù)據(jù)的預(yù)處理、模型類型的選擇和參數(shù)估計以及模型驗證和比較等功能［15］。

4 應(yīng)用實例

4.1 待辨識實驗數(shù)據(jù)

假設(shè)已知某實際系統(tǒng)在正弦信號作為輸入情況下的響應(yīng)如表1所示。

4.2 模型參數(shù)辨識

針對表1中的數(shù)據(jù)采用最小二乘法進行模型參數(shù)辨識，其中模型采用自回歸各態(tài)經(jīng)歷（ARX）模型，如圖2所示。經(jīng)過估算得到傳遞函數(shù)如圖3所示。

表1 系統(tǒng)輸入輸出數(shù)據(jù)

圖2 最小二乘法辨識參數(shù)設(shè)定

圖3 最小二乘法辨識結(jié)果

所以得到的傳遞函數(shù)為：

若針對表格中的數(shù)據(jù)采用近似最優(yōu)4階輔助變量法進行模型參數(shù)辨識，如圖4所示。經(jīng)過估算得到傳遞函數(shù)如圖5所示。

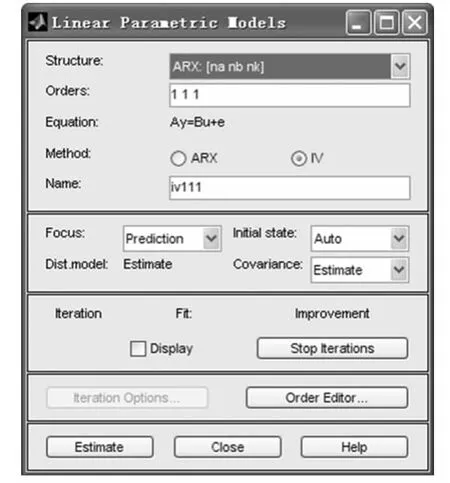
圖4 近似最優(yōu)4階輔助變量法辨識參數(shù)設(shè)定

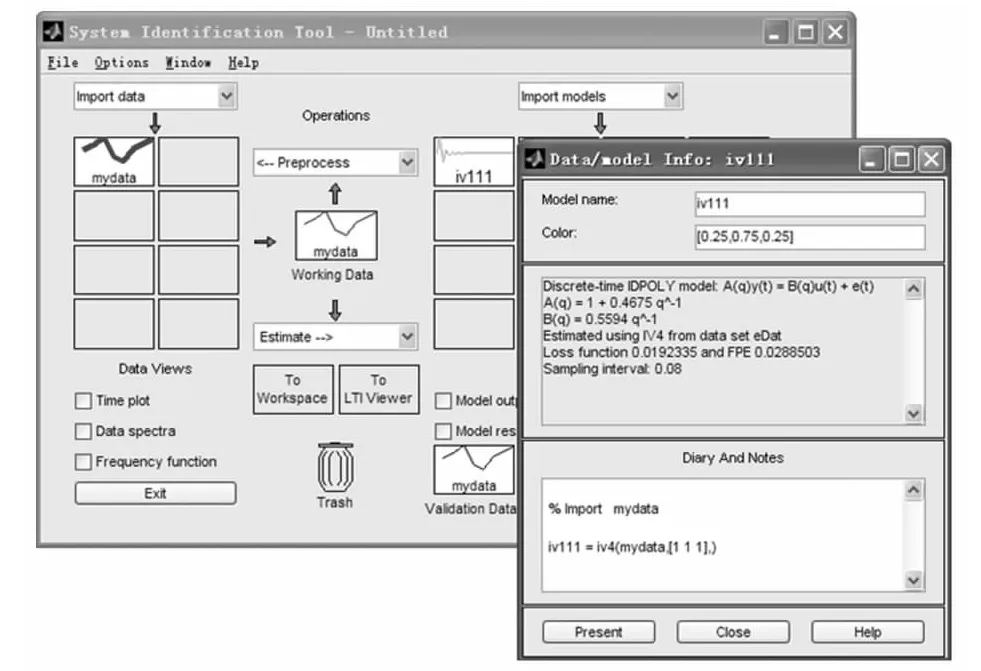
圖5 近似最優(yōu)4階輔助變量法辨識結(jié)果

所以得到的傳遞函數(shù)為：

4.3 模型驗證

經(jīng)過兩種方法的辨識得到的模型還要經(jīng)過驗證來證明其正確性。對兩種模型和實驗對象采取相同的輸入信號，觀察輸出信號，如果模型輸出和實際輸出幅度擬合很好就說明模型的正確性。最小二乘法所得模型輸出和實驗對象輸出對比如圖6所示，近似最優(yōu)4階輔助變量法所得模型輸出和實驗對象輸出對比如圖7所示。

從圖6和圖7所示結(jié)果可見兩種方法所得模型和實驗對象有較好的擬合效果，較好地完成了模型的辨識。而近似最優(yōu)4階輔助變量法所得模型擬合精度高于最小二乘法所得模型。當噪聲的模型結(jié)構(gòu)不好確定時，最優(yōu)4階輔助變量法更顯示出對系統(tǒng)辨識的優(yōu)越性。而MATLAB系統(tǒng)辨識工具箱中提供了各種各樣的系統(tǒng)辨識函數(shù)，為我們提供了一個可實現(xiàn)方便、快捷的系統(tǒng)建模方法。

圖6 最小二乘法辨識曲線擬合

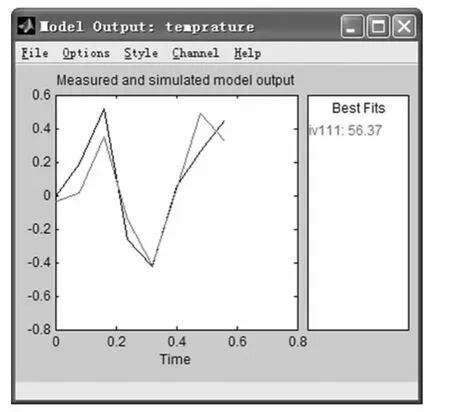
圖7 近似最優(yōu)4階輔助變量法辨識曲線擬合

［1］郭利輝，朱勵洪.基于 MATLAB的最小二乘法系統(tǒng)辨識與仿真［J］.許昌學(xué)院學(xué)報，2010，29（2）：24－27.

［2］陳杰，朱琳.基于混合最小二乘支持向量機網(wǎng)絡(luò)模型的非線性系統(tǒng)辨識［J］.控制理論與應(yīng)用，2010，27（3）：303－309.

［3］呂秋霞，李繼容.Matlab在系統(tǒng)辨識中的應(yīng)用［J］.儀器儀表用戶，2008，28（3）：60－61.

［4］ZADEH L A.From circuit theory to system theory［J］.Proc IRE，1962，50（5）：856－865.

［5］鄭劍翔.MATLAB系統(tǒng)辨識工具箱在系統(tǒng)控制設(shè)計中的應(yīng)用［J］.福州大學(xué)學(xué)報：自然科學(xué)版，2010，38（5）：703－707.

［6］劉靜紈.最小二乘法在系統(tǒng)辨識中的應(yīng)用［J］.北京建筑工程學(xué)院學(xué)報，2004，20（3）：19－22.

［7］王琳，馬平.系統(tǒng)辨識方法綜述［J］.電力情報，2011，63（4）：63－66.

［8］魯照權(quán)，胡焱東.具有限定記憶的輔助變量參數(shù)辨識法與仿真研究［J］.系統(tǒng)仿真技術(shù)，2009，5（2）：105－121.

［9］丁峰.系統(tǒng)辨識（4）：輔助模型辨識思想與方法［J］.南京信息工程大學(xué)學(xué)報：自然科學(xué)版，2011，3（4）：289－318.

［10］嚴曉久，周愛國.基于輔助變量法的系統(tǒng)參數(shù)辨識［J］.計算機應(yīng)用與軟件，2004，21（7）：127－129.

［11］史賢俊，廖劍.基于 MATLAB的廣義最小二乘參數(shù)辨識與仿真［J］.計算機與數(shù)字工程，2009（8）：173－175.

［12］鄭征，田書.基于 MATLAB的輔助變量法參數(shù)辨識與仿真［J］.機床與液壓，2006（12）：180－184.

［13］倪博溢，蕭德云.MATLAB環(huán)境下的系統(tǒng)辨識仿真工具箱［J］.系統(tǒng)仿真學(xué)報，2006，18（6）：1493－1496.

［14］李穎，林洪生.基于相對誤差的曲線最小二乘擬合［J］.沈陽師范大學(xué)學(xué)報：自然科學(xué)版，2012，30（3）：338－342.

［15］齊曉慧，田慶民.基于 Matlab系統(tǒng)辨識工具箱的系統(tǒng)建模［J］.軟件開發(fā)與應(yīng)用，2006，25（10）：88－90.