δ-方法在統計量漸近分布中的應用

周 小 雙

(德州學院 數學科學學院，山東 德州 253023)

統計量的分布稱抽樣分布，它在研究統計量的性質和評價一個統計推斷的優良性等方面十分重要. 近代統計學的創始人之一，英國統計學家Fisher R A 曾把抽樣分布、參數估計和假設檢驗列為統計推斷的3個中心內容. 因此尋求抽樣分布的理論與方法十分重要. 而一些統計量的精確分布我們無從得知，因此尋求統計量的漸近分布成了概率論與數理統計教學內容中的重要內容. δ -方法是概率論與數理統計教學中一個極其重要的結論，將δ -方法與其他結論有效的結合可以簡化一些統計量漸近分布的求解與證明. 本文主要通過實例強調說明了δ -方法在統計量漸近分布中的重要應用.

1 主要引理

引理1[1]38-39(Slutsky 引理)設和{Yn}是兩個隨機變量序列，若( c為常數)，則有：特別地，若則有(去0 律)；若，則有(去1 律).

引理2[1]36(中心極限定理)設隨機樣本 X1, X2, … ,Xn獨立同分布，且 EXi= μ，為樣本均值，則有

引理3[2]205-206(辛欽大數定律) 設 X1, X2,… 是一列獨立同分布的隨機變量，且數學期望存在： EXi= a ，i= 1,2,…則有

引理4[1]38設{ Xn}是隨機變量序列， c 為常數，則

引理5[1]41(連續映射定理)設為一隨機變量序列，且( c 為常數)，又函數g (·) 在點 c 處連續，則

2 δ -方法的證明

定理1 (δ -方法) 當 n →∞ 時，設數列 an→∞ ，隨機變量序列函數 f ( x )在x =b處存在二階連續導數，則有：

3) 若 f ′( b) = 0,f ′( b) ≠0，則

證明 主要應用Slutsky 引理. 當n →∞時:

3) 對βn進行二階Taylor 展開可得

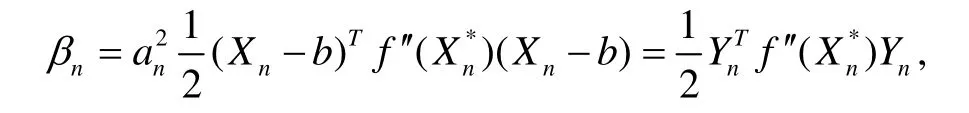
3 實例分析

例1 設X1, X2, …,Xn是來自兩點分布 b(1,θ )的隨機樣本，其中求樣本均值的函數的漸近分布.

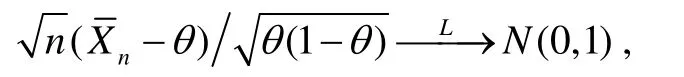
在δ - 方法中取 f ( x )= x(1 - x)，則 f ′ ( x) = 1- 2x 在 (0,1)上連續，取顯然 an→∞，則由δ-方法可知

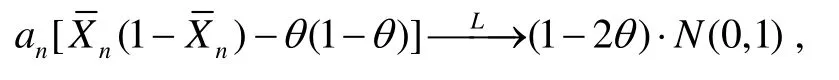
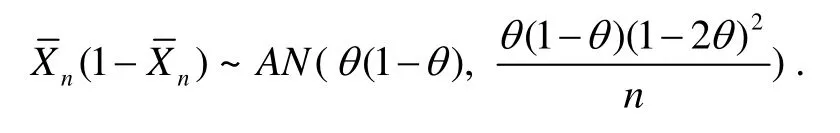
例……