現場XRF數據處理中多重分形方法研究

熊 超，葛良全，羅耀耀，米耀輝，徐立鵬

（1.成都理工大學 核技術與自動化工程學院，四川 成都 610059；2.成都理工大學 地學核技術四川省重點實驗室，四川 成都 610059；3.中國國土資源航空物探遙感中心，北京 100083）

0 前言

地球化學勘查方法是礦產勘查的重要手段［1］，化探異常上限值、下限值是區分背景區與異常區的基本指標，而計算異常上限值、下限值的準確性，也直接關系到下一步探礦工作開展的關鍵。長期以來，人們主要使用經典的統計學方法，以樣品數據呈正態分布為假設前提，通過計算數據的統計學參數（如均值、中位數、標準離差等）對異常進行篩選和評價［2］，但實際工作中的原始數據很難完全滿足正態分布或對數正態分布；為使其滿足正態分布，對原始數據進行的剔除和處理，又很難保持數據的完整性和真實性，使得傳統統計方法的使用存在一定的局限性。近年來，國內、外許多地質學家從不同角度認識到地球化學數據場具有多重分形的特點［2，4，6］。而分形方法為我們提供了利用較少參數描述復雜事物的一條捷徑［5，7］。此外，利用分形方法來處理地球化學數據，既考慮了數據的頻率分布特征和空間信息屬性，同時又符合地球化學數據場具有標度不變的自相似性特點［2～7］。作者在本文以新疆西天山托遜工區1∶50 000X熒光土壤化探數據為例，利用五段式擬合含量求和法來確定異常上限值、下限值。

1 多重分形方法

分形理論是以自然界和社會活動中廣泛存在的無序而具有內部自相似性的系統為研究對象，提取出確定性、規律性的參量，揭示復雜事物中新的深刻而定量的規律［10］。傳統的確定地球化學異常方法存在一定局限性，并從分形的觀點（地球化學背景和異常的形成是兩個獨立的過程）認為，地球化學背景值和異常值具有各自獨立的冪指數關系，并由此推導出一種多重分形分布［12］。

分形模型：

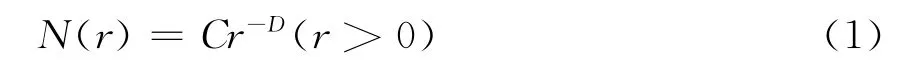
式（1）中，r為特征尺度；C＞0為比例常數；D＞0為一般分維數；N（r）＝N（≥r）為尺度大于等于r的和數。

設地球化學元素的值｛xi｝，i＝1、2、…、N、則：

將式（2）代入式（1），兩邊分別取對數，得到一元線性回歸模型：

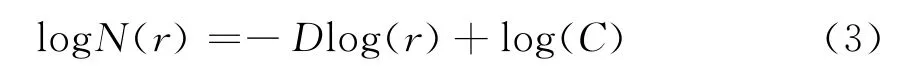
得到式（3）后采取最小二乘估計方法計算D的估計值，即維數：坐標散點大致分布在幾段直線附近，使用各段直線分別擬合的方法求取線性方程組并求解。目前使用較為廣泛的地球化學異常下限確定的分形方法主要有：含量頻數法、含量求和法、含量面積法等。

以往分形方法應用于地球化學異常數據處理，只能確定異常下限值，而對異常強度、負異常分布等信息的提取方法未有涉及，異常信息比較單一。DZ／T0011－91《1∶50 000地球化學普查規范》要求將異常分為低值區、低背景區、背景區、高背景區、高值區，且多重分形方法可以推廣到三段直線以上的情況，即地球化學數據中存在著多個無標度范圍，分三組以上的情形［3、8］。出于上述考慮，作者在本文采用含量求合法嘗試將分形圖擬合為五段直線以對應上述五個區域，通過各段擬合直線交點求取各部份異常上限和下限值。

2 分析方法

2.1 樣品的采集與測量

樣品采集過程是在工區內布置測線14條，點線距為50m×100m，采集距地表20cm左右的淋積層土壤化探樣品共432件。為降低測量時粒度效應對熒光強度的影響，樣品曬干后使用120目篩網進行過篩。各元素含量測試由成都理工大學自主研發的IED－2000P手提式多元素X熒光分析儀完成，測量時間設定為500s。其中As元素檢出限小于10μg／g，Sr元素檢出限小于100μg／g。

準確度是度量測量結果與“真值”間誤差的專業術語。現場X射線熒光分析儀的分析準確度是以標準物質為測量對象，依照DZ／T0011－91《1∶50 000地球化學普查規范》的準確度評估方法，用式（4）評價準確度

△LgC＝LgCi－LgCs （4）式中 Ci為樣品的儀器分析實測值；Cs為標準物質的推薦值。

選定標準樣品1個～3個，應用X熒光儀測定目標元素的含量，計算標樣推薦值C標與儀器實測值C測之間的平均對數偏差（X）與對數標準離差（λ值），計算公式為：

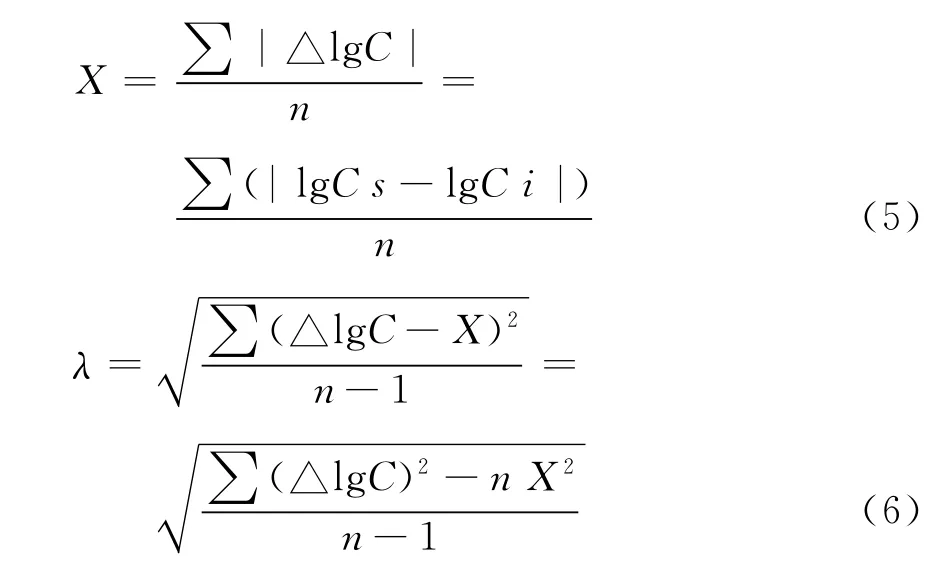
式中 n為測定的標準樣品的個數。

《規范》要求含量小于等于3倍檢出限含量時，X值小于等于0.25，λ值小于等于0.41；含量大于3倍檢出限含量時，X值小于等于0.2，λ值小于等于0.33。

標準樣測試所得X值與λ值見表1。

從表1中數據可以看出，As、Sr兩元素準確度均符合現場X熒光分析準確度檢查監控限要求。

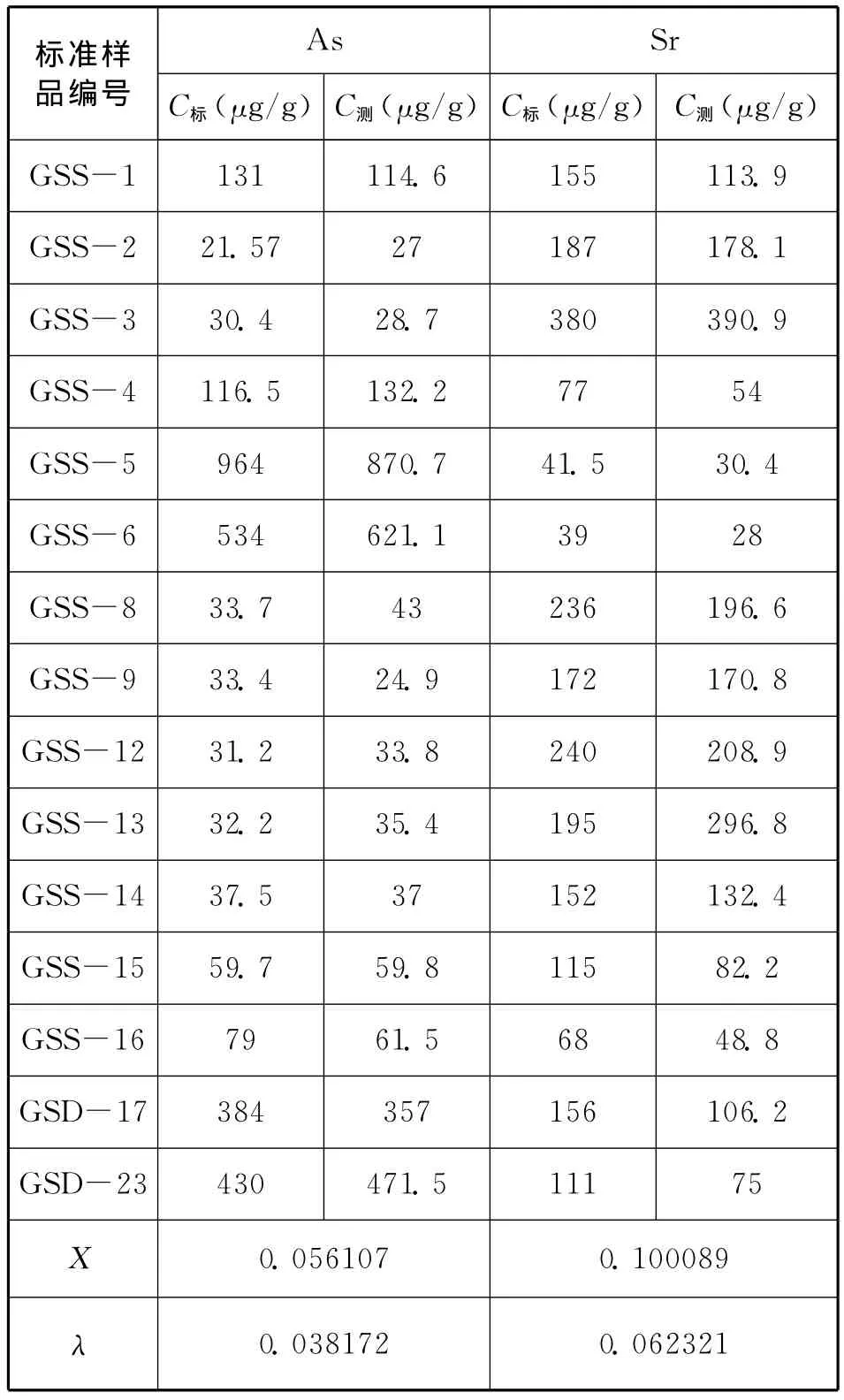
表1 元素準確度分析表Tab.1 Elements of accurate analysis table

2.2 數據分析

擬合過程與步驟：

（1）在各數據統計單元中，按照某一確定比例的間隔設定各元素含量值r，求出大于r的該元素全部樣本的含量和 N（r），得到 As、Sr兩組［r，N（r）］數據集（見表2及下頁表3）。

（2）將［r，N（r）］數據集均取自然對數后投影坐標散點圖。

（3）將散點圖中的點位大致分為五段，利用剩余平方和最小原則做線性擬合。擬合時為了將主觀人為因素對擬合精確度的影響盡量降低，這里采用統計方法中剩余平方和Ei（i＝1，2，3，…）最小原則對擬合的方程進行約束，以期提高異常界限點的精確度，約束方程如式（7）。

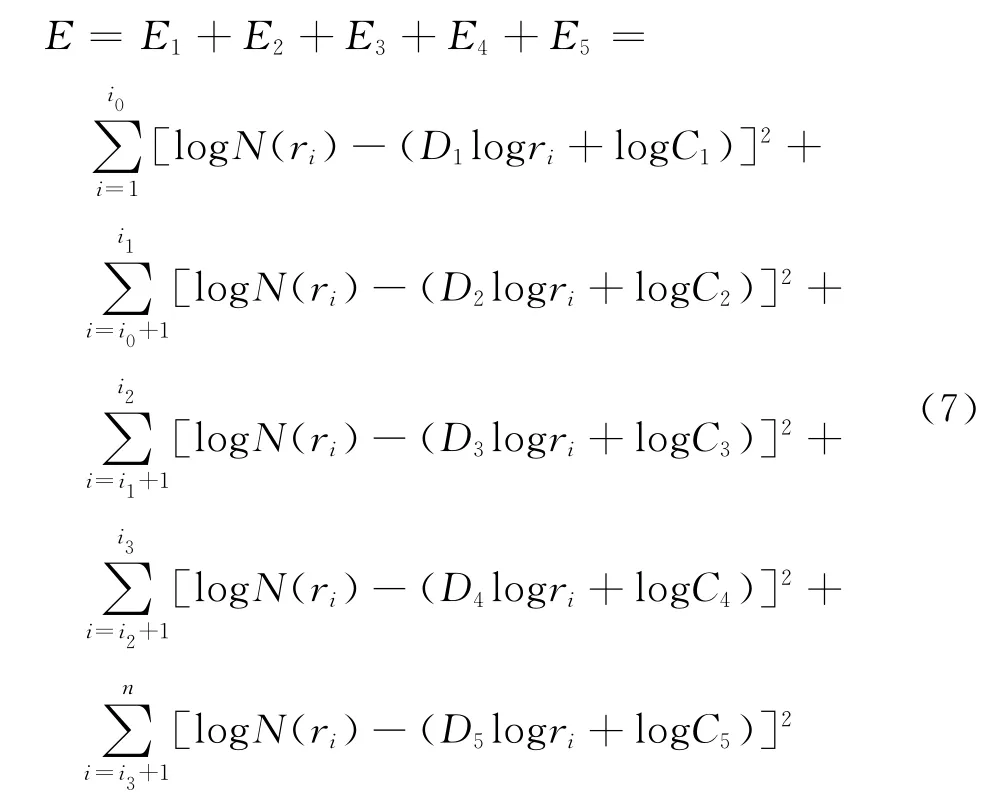
式中 i0、i1、i2、i3分別為擬合后從左至右五條直線的交點；D1、D2、D3、D4分別為擬合直線斜率的絕對值，即分維數。

擬合結果如后面圖1、圖2所示。

各段直線擬合后交點坐標如后面表4所示。

2.3 方法對比

傳統的統計方法是基于數據符合正態分布或對數正態分布的假設基礎之上，但長期化探工作的經驗表明，沒有絕對理想的采樣數據服從正態分布或對數正態分布。而對于測量數據不符合正態分布的情況，首要步驟是對原始測試數據進行常規的數據處理，即進行極異值（極高值、極低值）的迭代剔除處理，一般采用平均值X±3×均方差S為上限、下限迭代剔除，直至無極異數值可剔除為止。即所有處理后的數據均分布在X－3S與X＋3S之間，測試的背景數據，再以平均值加減二倍均方差（X±2S）計算異常上限、下限。計算結果如后面表5。

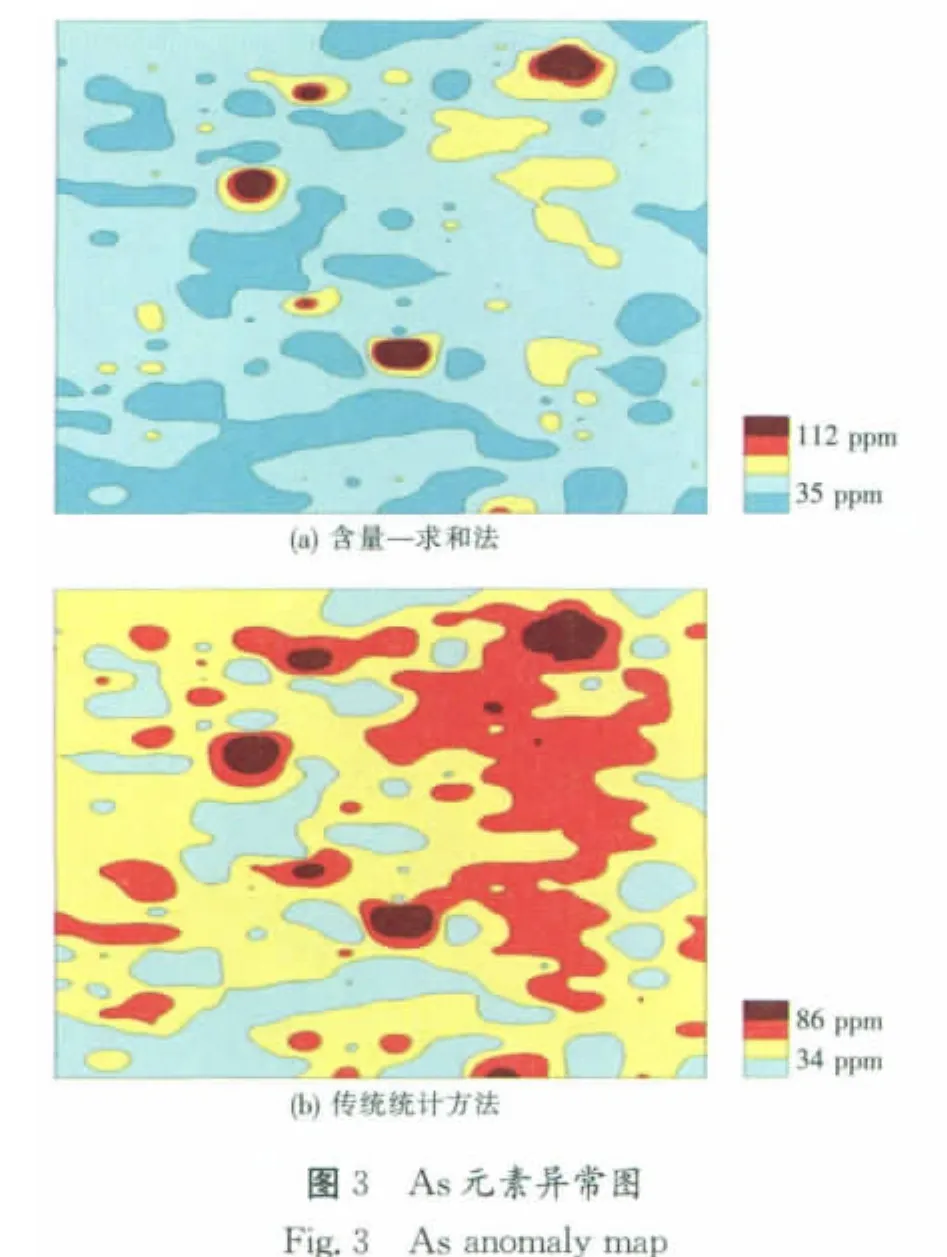
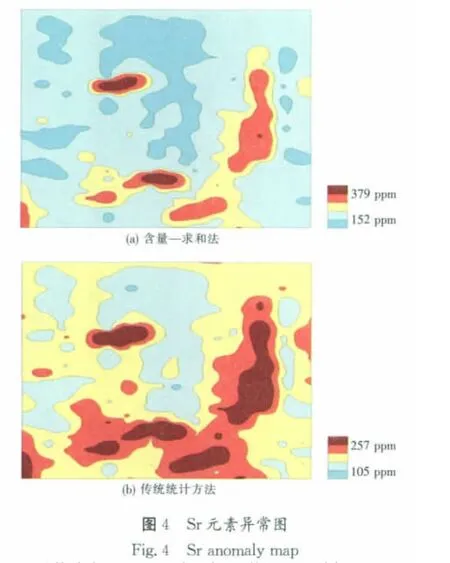
將兩種方法所圈定的異常通過MAPGIS軟件成圖的結果如后面的圖3及圖4所示。

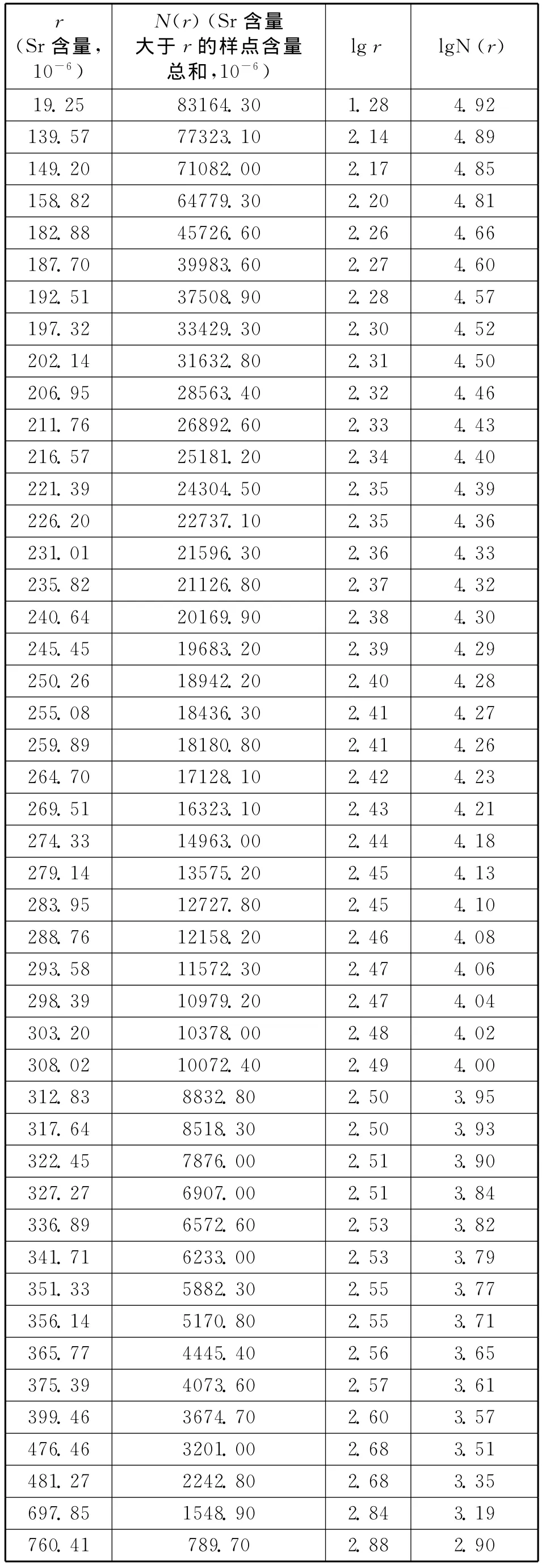
表2 利用含量—求和法確定Sr元素異常的統計參數Tab.2 Sr anomaly statistical parameter by content－summation method

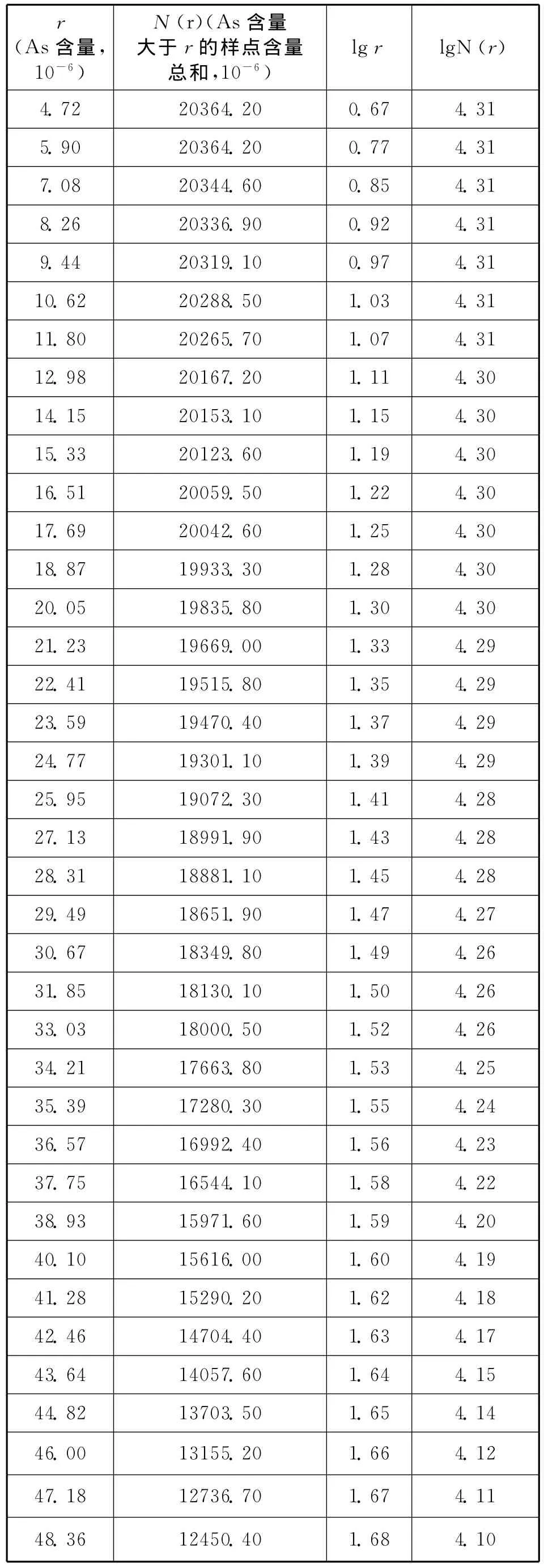
表3 利用含量—求和法確定As元素異常的統計參數Tab.3 As anomaly statistical parameter by content－summation method

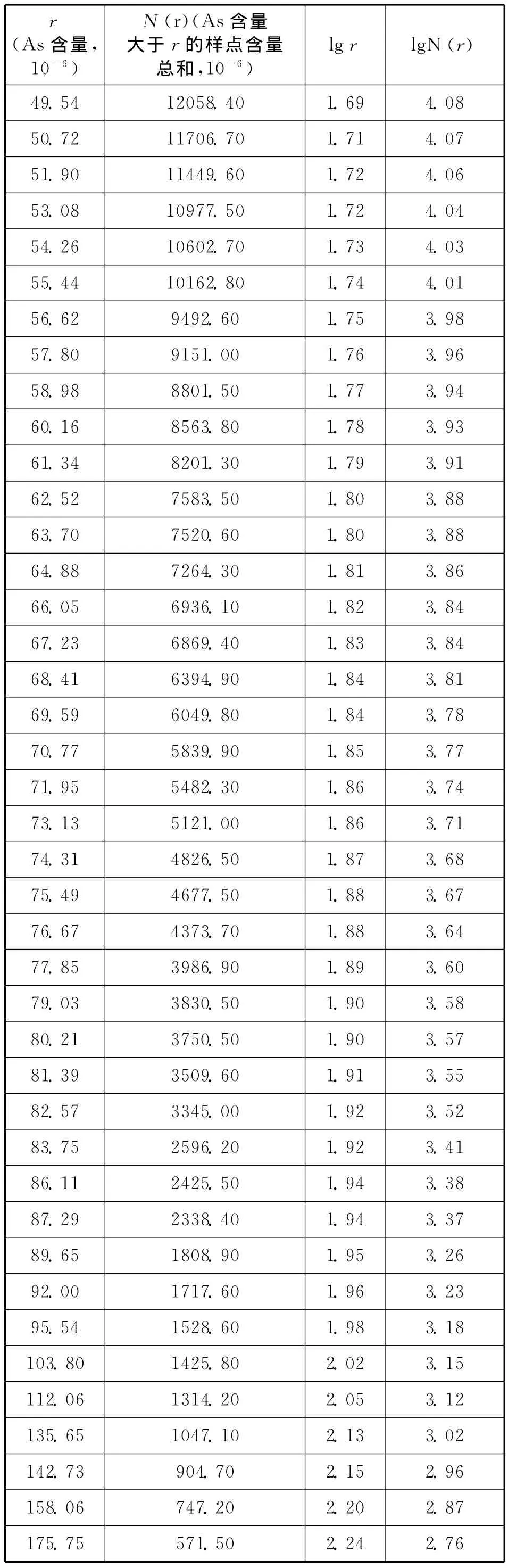
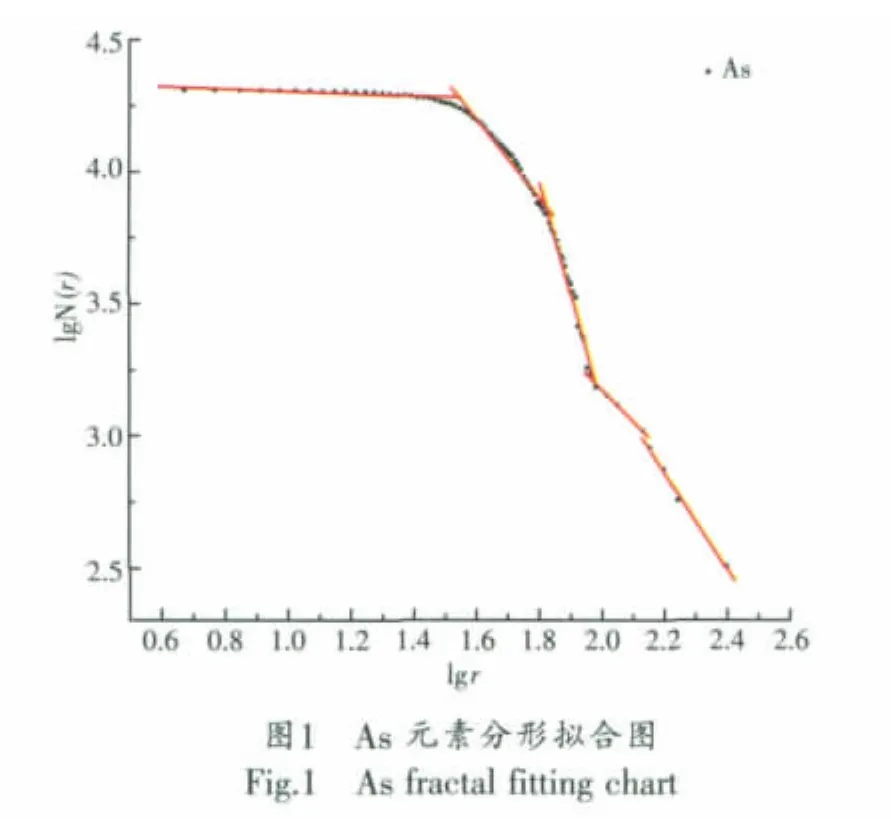
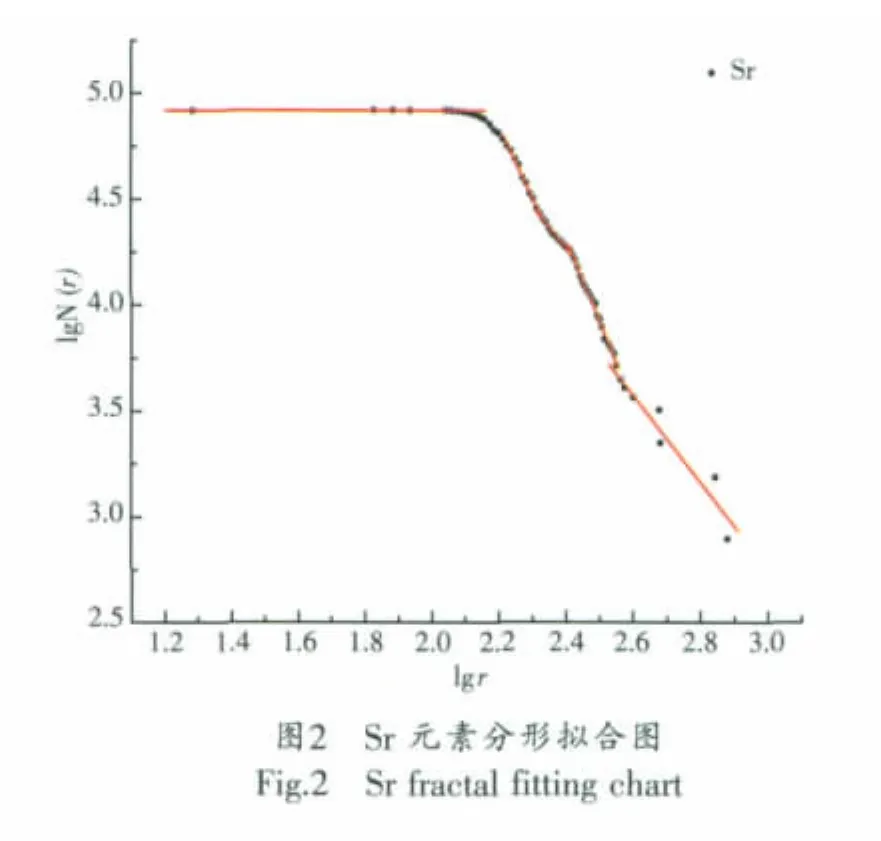
表4 含量求和法擬合的異常上限、下限值（單位：μg／g）Tab.4 Lower limit of positive anomaly and the upper limit of negative anomaly by content－summation method（unit：μg／g）

表5 傳統統計方法計算的異常上限、下限值（單位：μg／g）Tab.5 Lower limit of positive anomaly and the upper limit of negative anomaly by traditional statistics method（unit：μg／g）

3 異常解釋

由圖3發現：兩種方法圈定的工區As元素正異常范圍一致性較高，工區共出現四處規模較大的正異常：在圖3（a）中，As元素四處正異常周圍均有明顯的負異常環繞，即典型的正負異常相伴出現［9］，據此說明極有可能側分泌作用是As元素發生富集的主要原因；工區最南端出現一處較大規模的帶狀負異常，負異常中心未見正異常出現，且負異常走向與工區地質界限基本重合，推測為巖漿作用晚期交代所導致的負異常，成礦物質可能來自圍巖；而圖3（b）中未出現明顯的負異常，背景區范圍明顯大于圖3（a），這印證了傳統統計方法確定的異常下限值并非由全部數據來決定，而只是由背景數據決定，對度量一般值效果較好［10］。

在對比圖4（a）與圖4（b）后發現：使用含量求和法圈定出的正異常范圍，明顯小于傳統統計方法所確定的負異常；圖4（a）中部出現的大范圍Sr負異常位于含鈣質砂巖中，由于Sr離子半徑較小，呈現與Ca2＋十分相似的地球化學行為，較容易以游離形式（主要以重碳酸鹽、氯化物、硫酸鹽的形式）隨土壤溶液或地表水進行遷移，結果導致地層中大量Sr的淋溶［11］。圖4（a）工區底部出現的Sr異常恰好處于風成黃土、含鈣質砂巖與晶屑凝灰巖交界處，由于Sr的活動性比鈣小，在粘土礦物中比較穩定，造成了Sr在工區底部的第四紀覆蓋物邊緣富集的結果。

4 結果與討論

（1）多重分形方法對As元素的正異常的識別圈定與傳統統計方法的一致性較好，異常范圍基本相同。Sr元素使用多重分形方法確定的高背景值區和異常范圍則遠小于傳統統計方法，縮小了下一步異常查證的范圍，但可能會漏掉工區內某些弱小異常。

（2）多重分形方法對工區內負異常的識別效果較好，而傳統統計方法由于其偏重于描述背景數據的局限，導致工區內基本無負異常出現。建議在利用元素的貧化特征找礦時，應盡量避免使用化探規范推薦的傳統統計方法。

（3）在實際化探工作中，為了消除復雜的地質背景對異常信息提取造成的影響，可根據實際情況采用多種計算方法相結合，綜合分析，圈定有利成礦靶區。

［1］成秋明，張生元，左仁廣，等.多重分形濾波方法和地球化學信息提取技術研究與進展［J］.地學前沿，2009，16（2）：185.

［2］李長江，麻士華，朱興盛，等.礦產勘查中的分形、混沌與ANN［M］.北京：地質出版社，1999.

［3］徐明鉆，朱立新，馬生明，等.多重分形模型在區域地球化學異常分析中的應用探討［J］.地球學報，2010，31（4）：611.

［4］成秋明.多維分形理論和地球化學元素分布規律［J］.地球科學：中國地質大學學報，2000，25（6）：313.

［5］李錳，朱令人，龍海英.不同類型地貌的各向異性分形與多重分形特征研究［J］.地球學報，2003，24（3）：237.

［6］孫忠軍，礦產勘查中化探異常下限的多重分形計算方法［J］.物探化探計算技術，2007，29（1）：54.

［7］張建，王登紅，孫寶生，等.基于分形理論的成礦空間分析——以新疆東天山康古爾塔格金礦帶為例［J］，地球學報，2009，30（1）：58.

［8］申維.分形求和法及其在地球化學數據分組中的應用［J］.物探化探計算技術2007，29（2）：134.

［9］史長義，汪彩芳.區域次生地球化學負異常模型及其意義［J］.物探與化探1995，19（2）：104.

［10］戴慧敏，宮傳東，鮑慶中，等.區域化探數據處理中幾種異常下限確定方法的對比——以內蒙古查巴奇地區水系沉積物為例［J］.物探與化探2010，34（6）：782.

［11］賈耀鋒，毛龍江.黃土Rb、Sr地球化學研究新進展［J］.土壤通報2010，41（6）：1501.

［12］CHENG Q，AGTERBERG F P，Ballantyne S B.The separation of geochemical anomalies from backgrocund by fractal methods［J］.Journal of Exploration Geochemical，1994，51（2）：109.