基于齊次變換矩陣數(shù)值解的6自由度并聯(lián)機(jī)構(gòu)位姿正解解算

劉玉梅，曹曉寧，王秀剛，王帆，徐振，盧海隔

(1.吉林大學(xué)交通學(xué)院，吉林長(zhǎng)春130022;2.長(zhǎng)春軌道客車股份有限公司，吉林長(zhǎng)春130062)

與串聯(lián)機(jī)構(gòu)相比，并聯(lián)機(jī)構(gòu)的逆解求解容易，正解求解困難［1-2］.針對(duì)正解問題，學(xué)者們根據(jù)桿長(zhǎng)約束條件建立以位姿為變量的非線性方程組，利用同倫連續(xù)法、牛頓迭代、消元法、神經(jīng)網(wǎng)絡(luò)、遺傳算法、粒子群法等計(jì)算方法來求解［3］.對(duì)于基于齊次變換矩陣或普通變換矩陣的并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解牛頓迭代求解算法來說，由于該算法涉及到求解含有三角函數(shù)的非線性方程組問題而不易解決，并且每迭代一次，以三角函數(shù)形式表示的雅克比矩陣需更新一次，計(jì)算量龐大且復(fù)雜，嚴(yán)重影響了計(jì)算速度，不利于基于位姿反解的運(yùn)動(dòng)位姿控制進(jìn)行實(shí)時(shí)監(jiān)控及修正.

為進(jìn)一步提高位姿正解求解速度和收斂性，本文結(jié)合齊次變換矩陣元素正交關(guān)系及桿長(zhǎng)約束條件，構(gòu)建以齊次變換矩陣元素為變量的位姿正解模型，利用牛頓拉夫遜法逐次逼近齊次變換矩陣最優(yōu)數(shù)值解，再根據(jù)齊次變換矩陣元素與位姿變量對(duì)應(yīng)函數(shù)關(guān)系求解對(duì)應(yīng)位姿.

1 數(shù)學(xué)模型

6自由度并聯(lián)機(jī)構(gòu)是并聯(lián)機(jī)器人機(jī)構(gòu)中的一大類，是學(xué)者研究得最多的并聯(lián)機(jī)構(gòu)［4］，廣泛應(yīng)用在運(yùn)動(dòng)模擬器、六維力與力矩傳感器和并聯(lián)機(jī)床、微操作機(jī)器人等領(lǐng)域［5］.從完全并聯(lián)的角度出發(fā)，這類機(jī)構(gòu)必須具有6個(gè)或6個(gè)以上的運(yùn)動(dòng)鏈，如具有6個(gè)作動(dòng)器的Stewart并聯(lián)機(jī)構(gòu)，吉林大學(xué)研制的7個(gè)作動(dòng)器的6自由度并聯(lián)機(jī)構(gòu)，以及哈爾濱工業(yè)大學(xué)研制的8作動(dòng)器6自由度并聯(lián)機(jī)構(gòu)［6］，且隨著并聯(lián)機(jī)構(gòu)的日益發(fā)展及承載能力的要求，將來可能會(huì)出現(xiàn)具有更多支鏈的6自由度并聯(lián)機(jī)構(gòu).雖然在現(xiàn)有的并聯(lián)機(jī)構(gòu)中也存在擁有3個(gè)運(yùn)動(dòng)鏈的6自由度并聯(lián)機(jī)構(gòu)，但本文只研究具有6個(gè)或6個(gè)以上，12個(gè)以下的運(yùn)動(dòng)鏈的6自由度并聯(lián)機(jī)構(gòu).

結(jié)合不同形式的6自由度并聯(lián)機(jī)構(gòu)結(jié)構(gòu)特點(diǎn)，分別在6自由度并聯(lián)機(jī)構(gòu)的上平臺(tái)和下平臺(tái)上建立體坐標(biāo)系o-xyz及靜坐標(biāo)系O-XYZ，作動(dòng)器上鉸鏈點(diǎn)Ai(i=1，2…，n，n表示作動(dòng)器個(gè)數(shù)，6≤n≤12)在體坐標(biāo)系中的坐標(biāo)用向量形式表示為

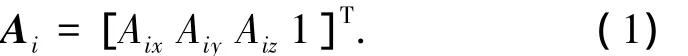
作動(dòng)器下鉸鏈點(diǎn)Bi(i=1，2…n)在靜坐標(biāo)系中的坐標(biāo)用向量形式表示為

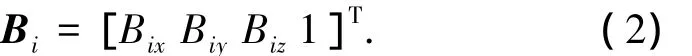
式中:Aix、Aiy、Aiz分別為第i個(gè)作動(dòng)器上鉸鏈點(diǎn)在體坐標(biāo)系沿x、y、z軸的坐標(biāo)值;Bix、Biy、Biz分別為第i個(gè)作動(dòng)器下鉸鏈點(diǎn)在靜坐標(biāo)系沿X、Y、Z軸的坐標(biāo)值.

當(dāng)上平臺(tái)運(yùn)動(dòng)后，任一上鉸鏈點(diǎn)在體坐標(biāo)系中的向量可以通過坐標(biāo)變換方法變換到該點(diǎn)在靜坐標(biāo)系中的向量，進(jìn)而上下鉸鏈點(diǎn)向量可表示為

式中:T為齊次變換矩陣，由于有限轉(zhuǎn)動(dòng)合成與轉(zhuǎn)動(dòng)次序有關(guān)，基于歐拉角的空間變換矩陣形式T可表述為12種形式，包括 TXYX、TYXY、TZXY、TXYZ、TYXZ、TZXZ、TXZX、TYZX、TZYX、TXZY、TYZY及 TZYZ形式.假設(shè)平臺(tái)的位姿用體坐標(biāo)系相對(duì)于靜坐標(biāo)系的廣義坐標(biāo) q=(q1，q2，q3，q4，q5，q6)來描述. 則ZYX空間齊次變換矩陣表示為［7］

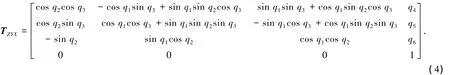
式中:qi(i=1，2，3)為體坐標(biāo)系相對(duì)于靜坐標(biāo)系的3個(gè)繞x、y、z軸的姿態(tài)角，qi(i=4，5，6)為體坐標(biāo)原點(diǎn)相對(duì)于靜坐標(biāo)系沿x、y、z3個(gè)坐標(biāo)軸的平移量.

n個(gè)作動(dòng)器的長(zhǎng)度可由上、下鉸鏈點(diǎn)間的距離來確定，因此由桿長(zhǎng)約束條件得

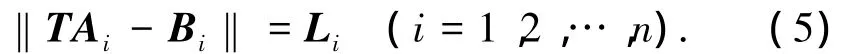
式中:Li為各個(gè)作動(dòng)器的長(zhǎng)度，i=1，2，…，n.

將式(5)進(jìn)行整理得

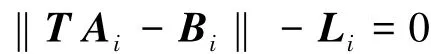
上式可以表示為

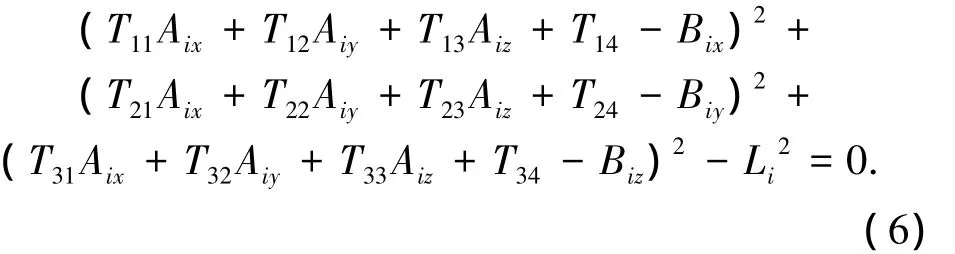
式中:Tij表示空間齊次變換矩陣中第i行、第j列元素，i=1，2，3，4，j=1，2，3，4.

空間齊次變換矩陣12種形式的前3階順序主子矩陣的每個(gè)元素都是qi(i=1，2，3)的三角函數(shù)，且元素之間呈現(xiàn)正交性［8-9］，用數(shù)學(xué)語言表達(dá)如下:

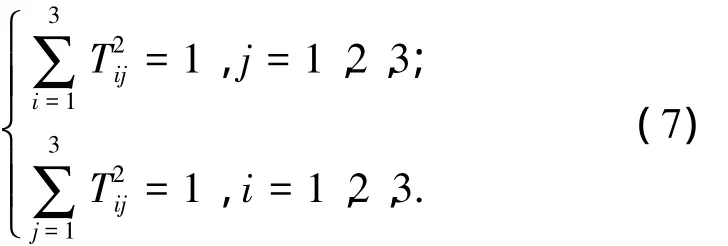
式(7)中有6個(gè)等式，分別為行或列的元素的平方和等于1.

結(jié)合含有6個(gè)自由度、n(6≤n≤12)個(gè)作動(dòng)器的并聯(lián)機(jī)構(gòu)幾何參數(shù)及空間運(yùn)動(dòng)學(xué)原理，由桿長(zhǎng)約束條件得到以矩陣元素為未知量的n個(gè)方程，并選取前3階順序主子矩陣元素關(guān)系式的任意12-n個(gè)聯(lián)立組成 12 個(gè)變?cè)?［T11，T12，T13，T14，T21，…，T33，T34］，12個(gè)多項(xiàng)式方程的方程組，從而將以位姿［q1，q2，q3，q4，q5，q6］為變量的正解問題隨之轉(zhuǎn)化為齊次矩陣元素為變量的求解問題.

為了使模型格式統(tǒng)一，添加虛擬作動(dòng)器桿長(zhǎng)ln+1，ln+2，…，l12，并將虛擬桿桿長(zhǎng)均設(shè)為 0，則由桿長(zhǎng)約束條件及任意選取的12-n個(gè)旋轉(zhuǎn)矩陣關(guān)系式聯(lián)立進(jìn)一步表示為

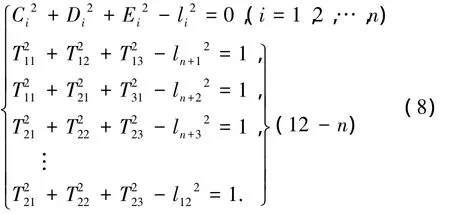
式中:

式(8)可進(jìn)一步抽象為

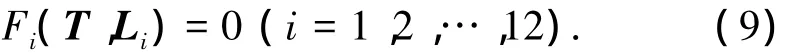
經(jīng)分析得知:式(8)實(shí)質(zhì)上是含［T11，T12，T13，T14，T21，…，T33，T34］12 個(gè)未知數(shù)，12 個(gè)桿長(zhǎng)的 12 個(gè)二次非線性方程組，其將上平臺(tái)實(shí)時(shí)位姿q=(q1，q2，q3，q4，q5，q6)的求解問題轉(zhuǎn)化為 ［T11，T12，T13，T14，T21，T22，T23，T24，T31，T32，T33，T34］的求解問題，雖然未知數(shù)個(gè)數(shù)由6個(gè)變?yōu)?2個(gè)，但同時(shí)避免了以姿態(tài)qi(i=1，2，3)為變量的三角函數(shù)的反復(fù)運(yùn)算，從而簡(jiǎn)化了求解過程.求得變換矩陣元素?cái)?shù)值解后，利用12種空間齊次變換矩陣與位姿變量之間的函數(shù)映射公式即可得到給定液壓缸的長(zhǎng)度下對(duì)應(yīng)的位姿q=(q1，q2，q3，q4，q5，q6).以 ZYX 旋轉(zhuǎn)空間齊次變換矩陣為例，空間齊次變換矩陣與位姿變量之間的映射關(guān)系如下:

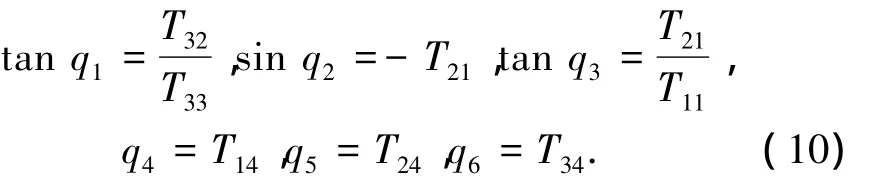
考慮到6自由度并聯(lián)機(jī)構(gòu)工作空間在-π/2，π/2(

)范圍內(nèi)，在此范圍內(nèi)正弦及正切都呈現(xiàn)單調(diào)遞增性，所以二者反函數(shù)取值具有單一性.

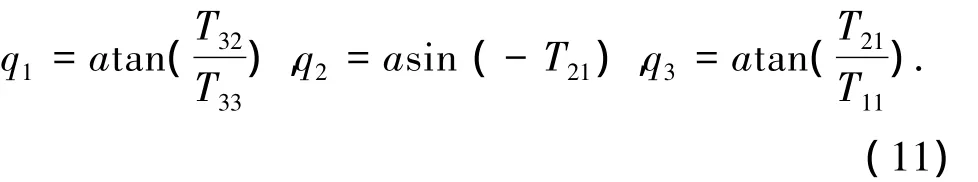
2 迭代求解

2.1 雅克比矩陣的確定

確定雅克比矩陣是利用牛頓迭代方法求得位姿正解數(shù)值解的關(guān)鍵［10］.經(jīng)研究證明，以齊次變換矩陣元素為變量的雅克比矩陣解析表達(dá)式只與聯(lián)立組成的非線性方程組有關(guān)，與齊次變換矩陣形式無關(guān).對(duì)于具有相同數(shù)目作動(dòng)器的并聯(lián)機(jī)構(gòu)而言，如果位姿正解非線性方程組選取一致，則雅克比矩陣解析表達(dá)式一致，故可廣泛應(yīng)用.由位姿正解方程組Fi(T，Li)=0(i=1，2，…，12)中各元素 Fi1，F(xiàn)i2，F(xiàn)i3對(duì)各變量 Tj求導(dǎo)，得到雅克比矩陣解析總表達(dá)式如下式所示.根據(jù)實(shí)際并聯(lián)機(jī)構(gòu)桿長(zhǎng)約束條件建立6自由位姿正解模型后，選取前3階順序主子矩陣正交性方程，進(jìn)而從雅克比矩陣解析總表達(dá)式查找對(duì)應(yīng)的Ji(i=1，2，…，12，表示行數(shù))構(gòu)成所求的雅克比矩陣解析表達(dá)式:

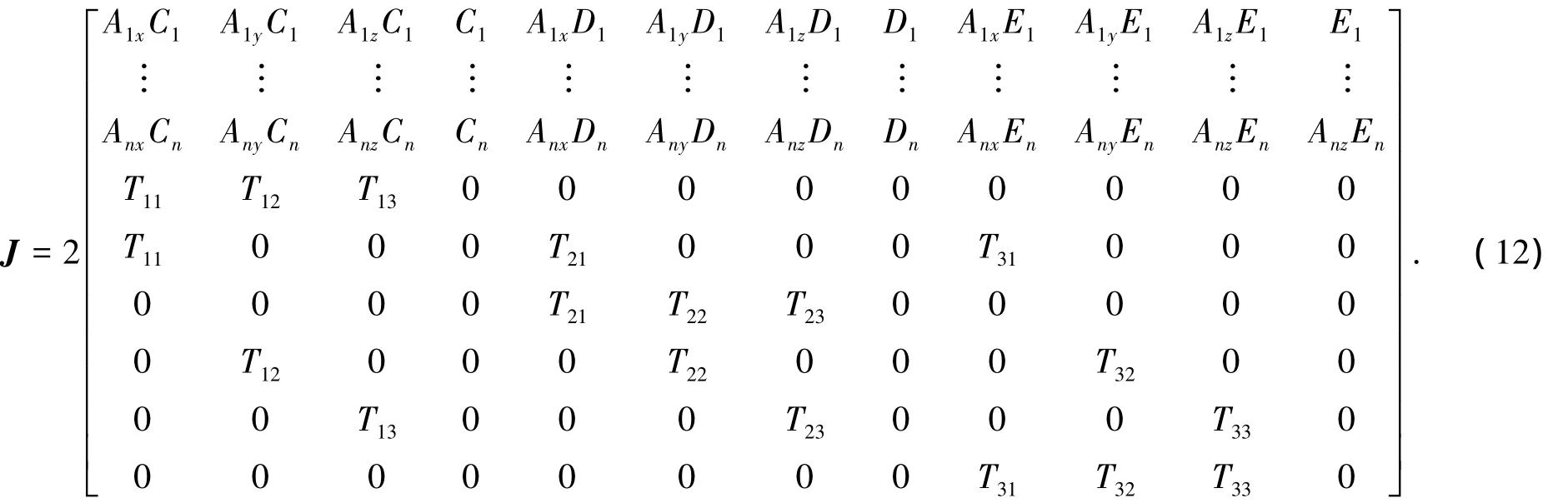
2.2 牛頓迭代算法

將式(9)作多元泰勒展開，取其線性部分，可得［11］

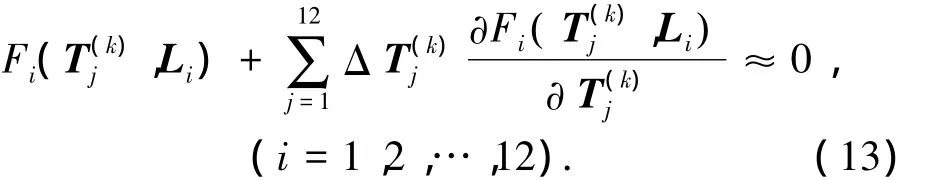
式中:k為迭代次數(shù);ΔT(k)j=T(k+1)j-T(k)j.

則上式經(jīng)整理表示為

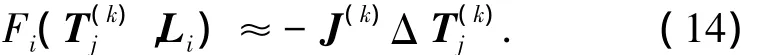
式(14)可以看作ΔT(k)j為未知數(shù)，J為系數(shù)矩陣的線性方程組.本文利用QR算法求解此線性方程組，得出方程組的解ΔT(k)j.計(jì)算步驟［12］如下:

1)選取位姿初值 q0及液壓缸伸縮量.將 q0代入到齊次變換矩陣公式得到對(duì)應(yīng)的T0.

2)確定以齊次變換矩陣元素為未知量的6自由度平臺(tái)位姿正解模型，并根據(jù)模型查閱雅克比矩陣總表，構(gòu)成雅克比矩陣J解析式，將變換矩陣初值T0及液壓缸伸縮量代入到式(9)和 J解析式中確定Fi(T(0)，Li)及 J(0)的取值.

3)利用QR算法求解下列線性方程組，得出方程組的解ΔT(k)j，

按照上述步驟反復(fù)迭代，每迭代一次根據(jù)最新得到的 T(k)對(duì) J及 Fi(T(k))更 新 一 次.將max(ΔT1，ΔT2，…，ΔT12)≤ ε(ε 為求解精度)作為算法結(jié)束運(yùn)行條件，按照下面公式完成迭代過程:

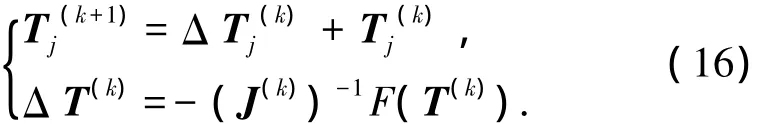
值得注意的是:由于齊次變換矩陣公式多樣性，即使在同一并聯(lián)機(jī)構(gòu)位姿初始值相同條件下，對(duì)應(yīng)的齊次變換矩陣元素初值也不同.

3 仿真模型及實(shí)例解算

利用Simulink搭建的位姿正解仿真模型，仿真模型如圖1所示，包括位姿初值輸入模塊、桿長(zhǎng)輸入模塊、位姿q與T轉(zhuǎn)化模塊、牛頓迭代模塊、T與位姿轉(zhuǎn)化模塊、輸出與顯示模塊.該模型在識(shí)別作動(dòng)器位移傳感器輸出的作動(dòng)器實(shí)時(shí)位移后，自動(dòng)實(shí)現(xiàn)位姿與齊次坐標(biāo)矩陣之間相互轉(zhuǎn)化、雅克比矩陣及位姿反解與實(shí)際桿長(zhǎng)之差的迭代更新，利用牛頓迭代法逐次逼近直至求得6自由度并聯(lián)機(jī)構(gòu)平臺(tái)位姿的最優(yōu)數(shù)值解，并將計(jì)算結(jié)果保存.該仿真模型可用于不同形式的、不同作動(dòng)器數(shù)目的6自由度并聯(lián)機(jī)構(gòu)位姿正解解算，具有廣泛的實(shí)用性，同時(shí)也為其他自由度并聯(lián)機(jī)構(gòu)位姿正解提供了借鑒作用.

以吉林大學(xué)汽車運(yùn)輸研究所設(shè)計(jì)并開發(fā)的具有7作動(dòng)器的3個(gè)軸向6自由度運(yùn)動(dòng)平臺(tái)為例，利用本文提出的基于齊次變換矩陣數(shù)值解的6自由度平臺(tái)位姿正解解算方法實(shí)現(xiàn)了位姿正解解算.取位姿初始值 q=(0，0，0，0，0，3 910).7 個(gè)液壓缸對(duì)應(yīng)長(zhǎng)度用向量 表 示 為 L=(2 940，2 940，2 920，2 920，2 730，2 730，2 920)，設(shè)置誤差精度為 1×10-5，運(yùn)行位姿正解仿真模型完成迭代過程，迭代4次后就已經(jīng)滿足誤差精度要求，結(jié)果為迭代過程耗時(shí)為0.0141 s，以位姿為變量的傳統(tǒng)牛頓迭代計(jì)算方法耗時(shí)為0.022 46 s，相比可節(jié)省0.005 s時(shí)間，2種方法結(jié)果均為 q=(0.025，0，0，0.015 8，0.178 2，3 920)，進(jìn)而驗(yàn)證本文提出的解算方法的高效性以及實(shí)用性.

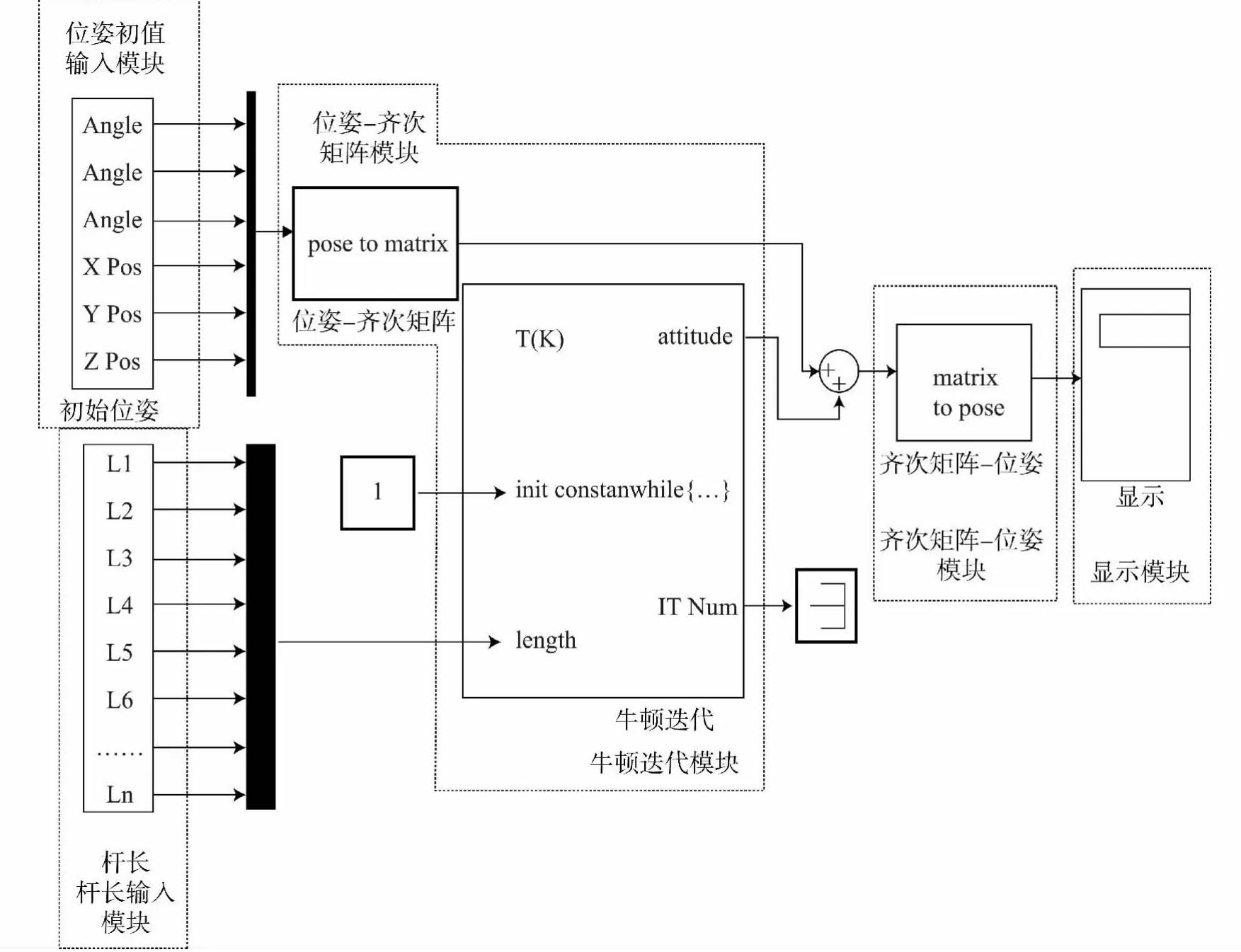
圖1 位姿正解仿真模型Fig.1 The forward kinematics simulation model

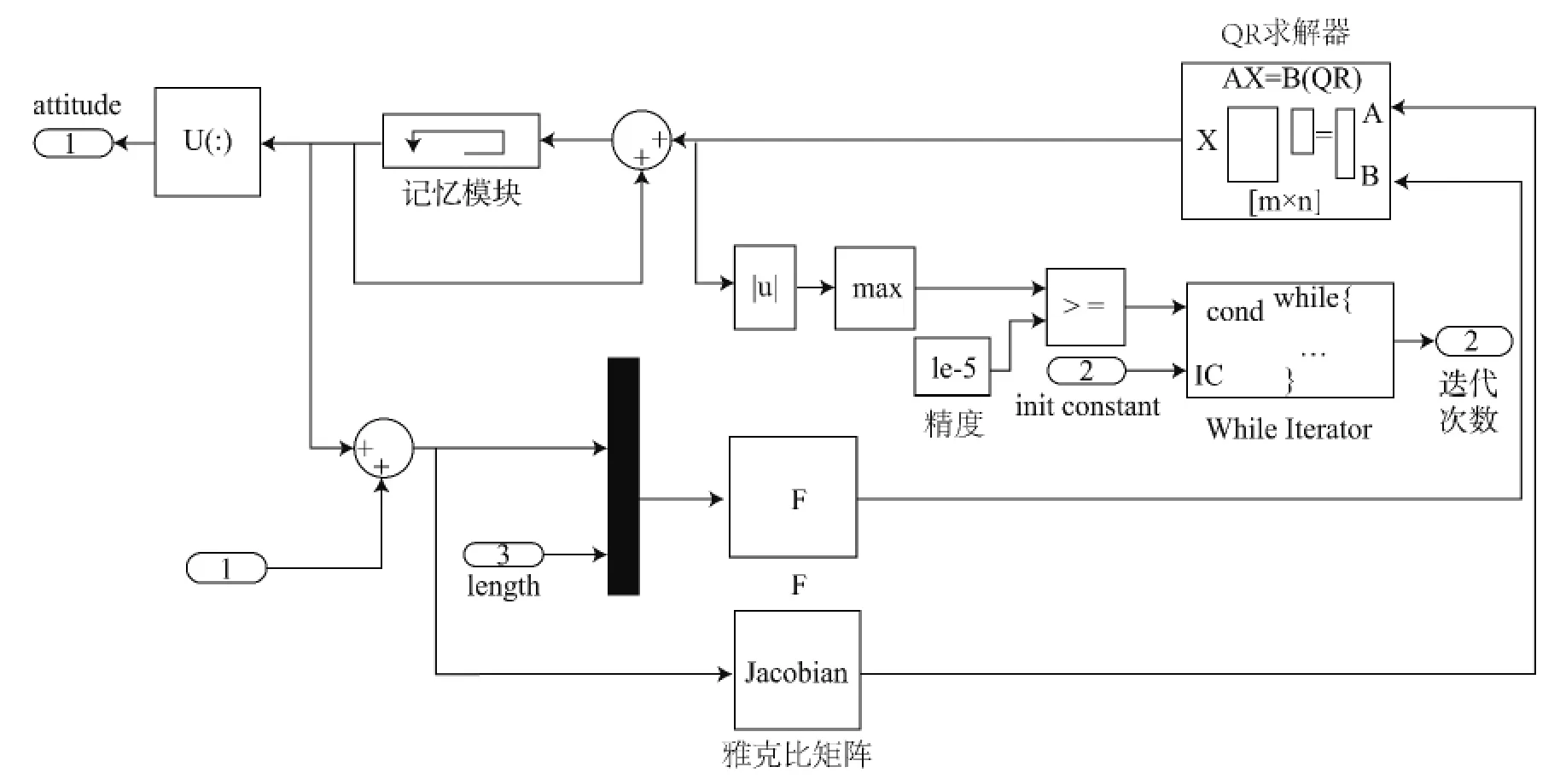
圖2 牛頓迭代模塊Fig.2 The New ton iteration module

4 結(jié)論

1)本文研究的以齊次變換矩陣元素為變量的位姿正解解算方法比以位姿為變量的傳統(tǒng)計(jì)算方法耗時(shí)少.2)該方法可服務(wù)于不同形式、不同作動(dòng)器數(shù)目、不同齊次變換矩陣形式的6自由度并聯(lián)機(jī)構(gòu)位姿正解，實(shí)用性強(qiáng).3)由于篇幅有限，文中列舉的實(shí)例較少，今后研究中應(yīng)選取不同作動(dòng)器數(shù)目、不同齊次變換矩陣形式的6自由度并聯(lián)機(jī)構(gòu)位姿正解進(jìn)行研究.

［1］高洪，趙韓.并聯(lián)機(jī)器人機(jī)構(gòu)學(xué)理論研究綜述［J］.安徽工程科技學(xué)院學(xué)報(bào):自然科學(xué)版，2006，21(1):73-79.GAO Hong，ZHAO Han A review about theory of mechanism for parallel robotics［J］.Journal of Anhui University of Technology and Science，2006 ，21(1):73-79.

［2］ZHOU Hui，CAO Yi，ZHANG Qiuju.The research on direct kinematic problem of a special class of the Stewart-Gough manipulators［C］//Proceedings of 2008 IEEE International Conference on Mechatronics and Automation.Takamatsu，Japan:Inst of Elec and Elec Eng Computer Society，2008:971-976.

［3］陳長(zhǎng)憶，車林仙.應(yīng)用粒子群算法的3-RPS并聯(lián)機(jī)器人機(jī)構(gòu)位置正解［J］.現(xiàn)代制造工程，2006，(5):77-79.CHEN Changyi，CHE Linxian.Forward position analysis of 3-RPS in-parallel manipulators based on particle swarm optimization［J］.Modern Manufacturing Engineering，2006，(5):77-79.

［4］李立，張劍，陳永，等.同倫迭代法的研究及其應(yīng)用于機(jī)構(gòu)學(xué)問題的求解［J］.西南交通大學(xué)學(xué)報(bào):自然科學(xué)版，2000，35(1):57-60.LILi，ZHANG Jian，CHEN Yong，et al.On the homogony iteration method and its application in the mechanism problems［J］.Journal of Southwest Jiaotong University，2000，35(1):57-60.

［5］BOUDREAU R，TURKKAN N.Solving the forward kinematics of parallel manipulators with a genetic algorithm［J］.Journal of Robotic Systems，1996，13(2):111-125.

［6］關(guān)廣豐.液壓驅(qū)動(dòng)六自由度振動(dòng)試驗(yàn)系統(tǒng)控制策略研究［D］.哈爾濱:哈爾濱工業(yè)大學(xué)，2007:29.GUAN Guangfeng.Control strategy of hydraulically driven 6-DOF vibration test system［D］.Harbin:Harbin Institute of Technology，2007:29.

［7］GALLARDO J，LESSO R，RICO JM，et al.The kinematics of modular spatial hyper-redundant manipulators formed from RPS-type limbs［J］.Robotics and Autonomous Systems，2011，58(1):12-21.

［8］程世利，吳洪濤，王超群，等.基于正交補(bǔ)的6-3 Stewart并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解［J］.中國(guó)機(jī)械工程，2011，22(5):505-508.CHENG Shili，WU Hongtao，WANG Chao qun，et al.Forward kinematics analysis of 6-3 Stewart parallel mechanisms based on orthogonal complement method［J］.Journal of Mechanical Engineering，2011，22(5):505-508.

［9］程永倫，朱世強(qiáng)，劉松國(guó)，等.基于旋轉(zhuǎn)子矩陣正交的6R機(jī)器人運(yùn)動(dòng)學(xué)逆解研究［J］.機(jī)器人，2008，30(2):160-164.CHENG Yonglun，ZHU Shiqiang，LIU Songguo，et al.Inverse kinematics of 6R robots based on the orthogonal character of rotation sub-matrix［J］.Robot，2008，30(2):160-164.

［10］賈軍艷.機(jī)構(gòu)運(yùn)動(dòng)分析與求解雅可比矩陣的計(jì)算機(jī)模擬法及應(yīng)用［D］.秦皇島:燕山大學(xué)，2006:15-18.JIA Junyan.Computer simulation approach for solving Jacobian and kinematic of mechanisms and application［D］.Qin huangdao:Yanshan University，2006:15-18.

［11］YANG Chifu，HUANG Qitao，OGBOBE P O，et al.Forward kinematics analysis of parallel robots using global Newton-Raphson method［C］∥Proceedings of 2009 2nd International Conference on Intelligent Computing Technology and Automation.Hunan，China:IEEE Computer Society，2009:407-410.

［12］TAROKH M，KEERTHIK，LEE M.Classification and characterization of inverse kinematics solutions for anthropomorphic manipulators［J］.Robotics and Autonomous Systems，2010，58(1):115-120.