一個新混沌系統的脈沖控制與完全同步

張群嬌

?

張群嬌

(武漢紡織大學 數學與計算機學院, 湖北 武漢 430073)

本文研究了文獻[12]中提出的一個新混沌系統的脈沖控制與完全同步問題。基于脈沖控制的方法，得到了保證脈沖控制的混沌系統和同步誤差系統在原點全局漸近穩定的一些準則。最后，數值仿真的結果證實了所提方法的有效性和可行性。

脈沖控制；完全同步；混沌系統

自從Ott 和Pecora關于混沌控制和同步的開創性工作以來[1,2], 在過去的幾十年里，混沌的控制與同步問題一直是非線性科學領域的研究熱點之一。人們先后提出了各種控制策略用于解決混沌的控制問題，如反饋控制，自適應控制，滑模控制，脈沖控制等等[3-11]。

事實上，由于脈沖控制的方法對于處理那些不能經受連續擾動的系統是有效的，并且，在系統同步的過程中，響應系統只需在離散的時刻接受來自驅動系統變量的信息，它顯得更加地受歡迎。也因此，它已經廣泛地應用于控制和同步混沌系統[8-11]。另外，從驅動系統到響應系統傳輸的信息量的驟減也使得這種方法在許多實際應用中更加有效用。

本文主要研究了如何利用脈沖控制的方法來穩定和同步一個新提出的混沌系統，在脈沖間隔變化的情形，得到了保證脈沖控制的混沌系統全局漸近穩定和同步的一些充分條件. 最后, 數值仿真的結果闡述了理論結果的正確性。

1 混沌系統的描述

在文獻[12]中，Abooee等人提出了一個新的混沌系統，系統描述如下

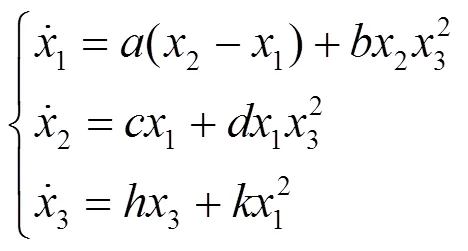
圖1 新的混沌系統的吸引子

2 新混沌系統的脈沖穩定控制

把方程(1)所刻畫的混沌系統的線性部分與非線性部分分開, 重寫如下

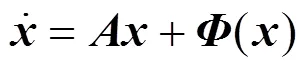
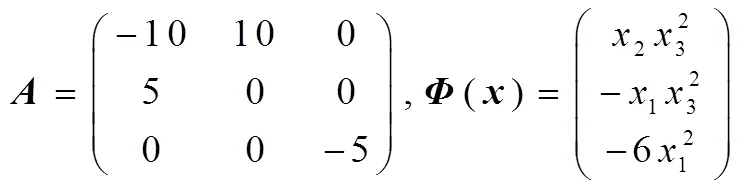
設計脈沖控制的系統方程形式如下

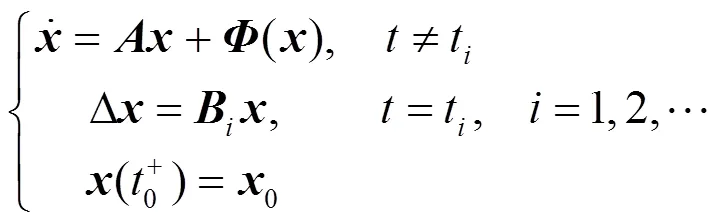
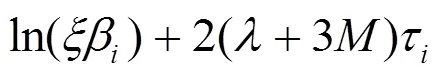
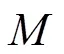
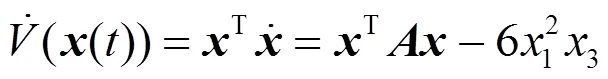
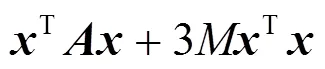
這意味著

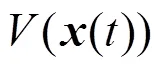
另一方面，從系統（4）的第二個方程可得

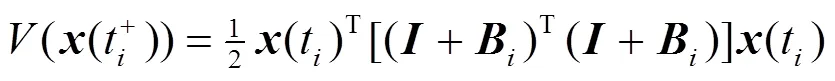
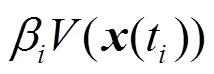
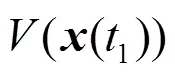
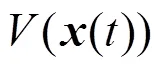
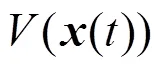
根據不等式（5）可知

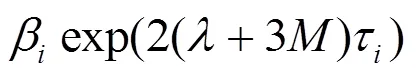
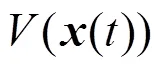
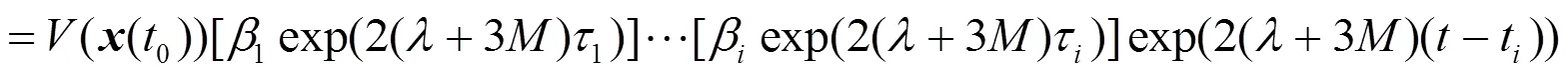
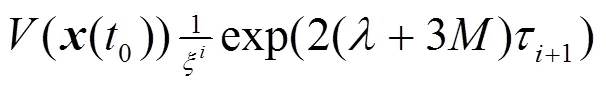
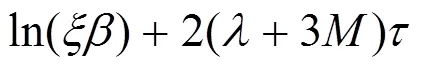
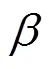
3 新混沌系統的脈沖完全同步

視方程（2）為驅動系統，設計脈沖控制的響應系統由下列脈沖方程刻畫

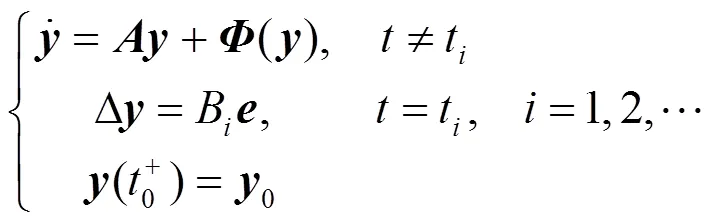
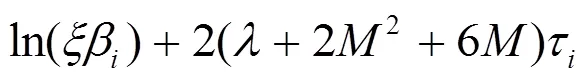
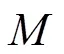
證明：由方程（2）和（12）,可得脈沖同步的誤差系統

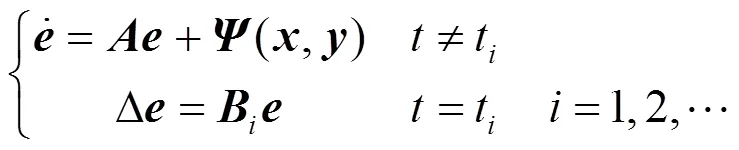
這里

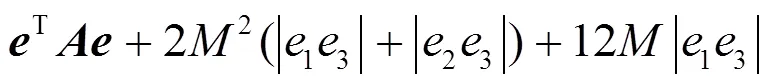
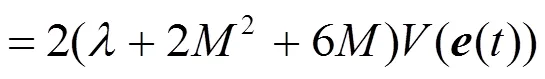
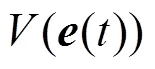
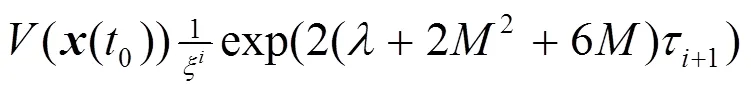
這意味著系統（14）的平凡解在原點是全局漸近穩定的。從而，脈沖控制的系統（12）與（2）就是全局漸近同步的。

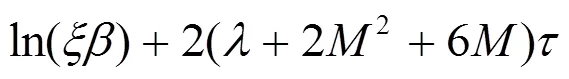
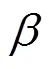
4 數值仿真

為了闡明所提方法的有效性和可行性, 這一部分給出了一些數值仿真的結果。

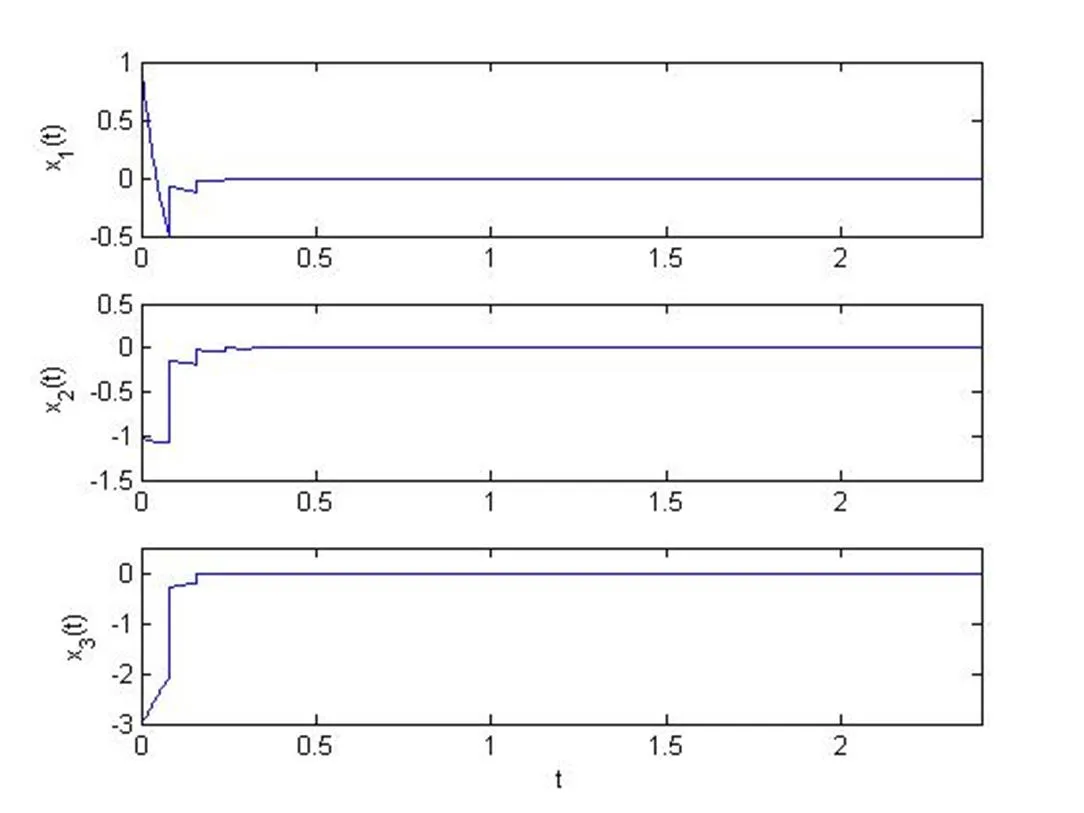
圖2 ,時脈沖穩定的系統狀態

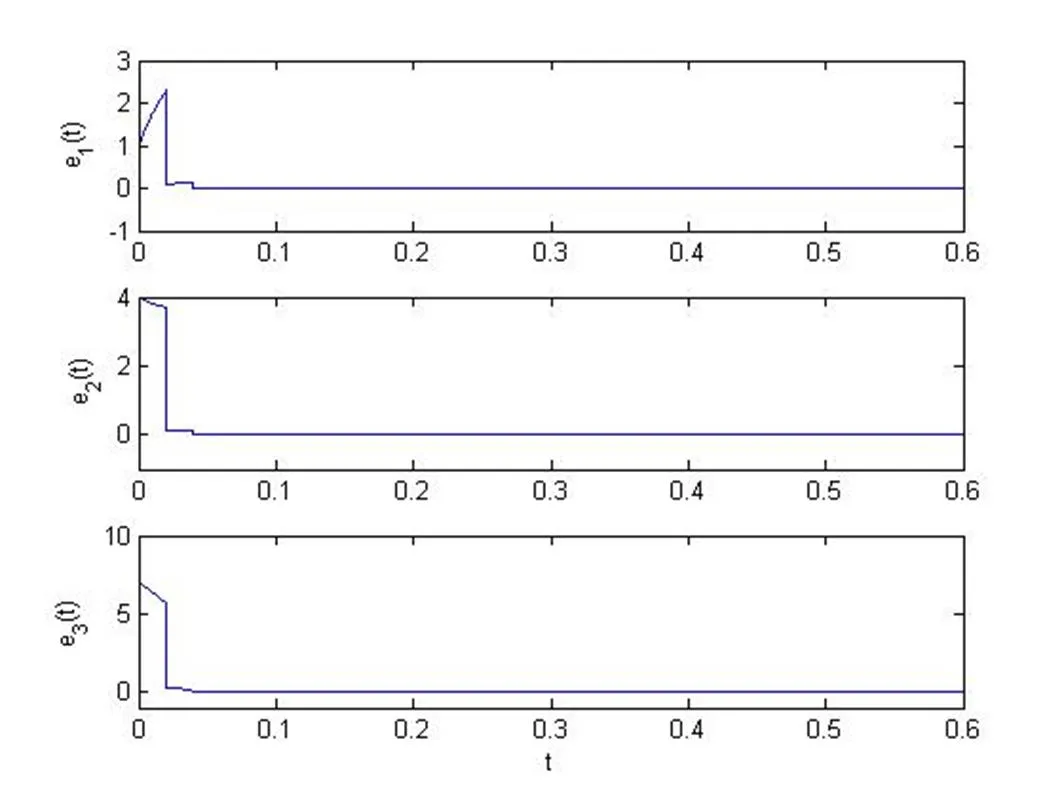
圖3 ,時脈沖同步系統的誤差

5 結論

本文研究了一個新的混沌系統的脈沖控制與同步問題，在脈沖間隔變化的情況得到了保證脈沖控制系統全局穩定和同步的一般性條件，并給出了特殊情形下的相應推論。最后，一些數值仿真的結果證實了所得的理論結果的正確性。

[1] Ott E, Grebogi C, Youke J A．Controlling Chaos[J]．Phys Rev Lett, 1990, 64: 1196-1199.

[2] Pecora L M, Carroll T L．Synchronization in Chaotic Systems[J]．Phys Rev Lett, 1990, 64: 821-824.

[3] Wang G, Yu X, Chen S．Chaos Control, Synchronization and its Application[M]. Beijing: National Defence Industry Publishing House, 2001.

[4] Wang C, Ge S．Adaptive Synchronization of uncertain chaotic System via backstepping Design[J]．Chaos, Solitons and Fractals, 2001, 12:1199-1206.

[5] Chen M, Han Z． Controlling and synchronizing chaotic genesio system via nonlinear feedback control[J]．Chaos, Solitons and Fractals, 2003, 17: 709-716.

[6] Chen S, Lü J．Parameters identification and synchronization of chaotic systems based on adaptive control[J]．Phys Lett A, 2002, 299: 353-358.

[7] Yan J, Yang Y, Chiang T, et al．Robust synchronization of unified chaotic systems via sliding mode control[J]．Chaos, Solitons and Fractals, 2007, 34:947-54 .

[8] Hu M, Yang Y, Xu Z. Impulsive control of projective synchronization in chaotic systems[J]. Phys Lett A, 2008, 372:3228–3233.

[9] Li C, Liao X, Zhang X. Impulsive synchronization of chaotic systems[J]．Chaos, 2005,15:023104.

[10] Chen S, Yang Q. Impulsive Control and Synchronization of Unified Chaotic System[J]．Chaos, Solitons and Fractals, 2004, 20: 751-758.

[11] Chen J, Liu H, Lu J, et al. Projective and lag synchronization of a novel hyperchaotic system via mpulsive control [J]．Commun Nonlinear Sci Numer Simulat, 2011,16 :2033-2040.

[12] Abooee A, Yaghini-Bonabi H, Jahed-Motlagh M. Analysis and circuitry realization of a novel three-dimensional chaotic system [J]．Commun Nonlinear Sci Numer Simulat, 2013,18:1235-1245.

Impulsive Control and Complete Synchronization of a Novel Chaotic System

ZHANG Qun-jiao

(College of Mathematics and Computer Science, Wuhan Textile University, Wuhan Hubei 430073, China)

The impulsive control and complete synchronization is investigated for a novel chaotic system [12]. Based on the impulsive method，some criteria are derived for the stability and synchronization of the impulsively controlled system. Finally, some numerical simulations are given to verify the effectiveness of the proposed theoretical results.

Impulsive Control; Complete Synchronization; Chaotic System

O 322

A

2095－414X(2013)03－0043－04

張群嬌（1980-），女，副教授，研究方向：混沌控制與同步，復雜動力系統.

國家自然科學基金資助項目(11271295)，湖北省教育廳科研項目（D20131602），武漢紡織大學校基金項目（2012）.