基于Copula函數的部件相關串聯機械系統可靠性分析

劉 喆，陶鳳和，賈長治

（軍械工程學院，河北 石家莊 050003）

0 引 言

武器裝備是作為一個整體系統在戰場上使用的，需要經常考慮它整體系統的可靠性指標。由于實驗條件的限制，只能假設裝備各個構件是相互獨立的，從而對這些構件單獨進行試驗，根據獨立性假設計算獲得系統的可靠性。

在裝備的實際使用過程中，周圍的環境因素、使用工況等同時作用于裝備整體，這必將造成零部件的可靠性有共同的發展趨勢，即各部件有著一定的相關性，此時仍采用獨立性假設是不合適的；因此，如何根據裝備各構件獨立的可靠性試驗數據得出具有相關性的串聯機械系統的可靠性，是本文研究的目的。

在現代的可靠性研究中，一種常用手段是隨機模擬的方法，然而該方法對算法、建模精度、模擬次數等要求較高，同時由于抽樣方法的不同，有可能導致偏差較大。隨機向量的聯合分布函數是刻畫隨機向量概率性質的重要工具之一，它包含了兩方面的信息：一是變量的邊緣分布信息，另一個是變量間相關結構的信息。邊緣分布信息相對容易獲得，即對部件單獨進行試驗可以得到部件的邊緣分布，但是變量間相關結構的信息很難獲取。如果能夠在聯合分布函數中除去邊緣分布的信息，那么就僅剩下了相關結構的信息。同時，如果引入Copula函數來構造多元隨機變量的聯合分布函數，將有利于解決相關部件的系統可靠度求解的問題。

1 Copula函數的定義和基本性質

1959年Sklar[1]最早提出Copula的概念：Copula是由一維隨機變量的概率積分變換引入的。對于一維的連續型隨機變量x，如其有分布函數F（x），由概率積分變換得到的 F（x）是服從[0，1]上的均勻分布，則一個二維Copula是滿足以下條件的一個函數：

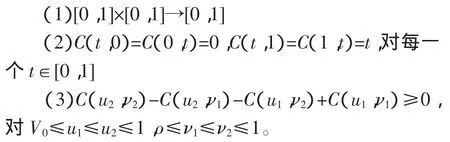
Sklar通過定理[2]說明，若X、Y是具有聯合分布函數H（x，y）的隨機變量且邊緣分布函數分別是F（x），G（y），則對所有的 x、y存在唯一的與之對應的Copula 使：H（x，y）=C（F（x），G（y））。Copula 將 X、Y的聯合分布函數H（x，y）與其邊緣分布函數聯系起來，展現了聯合分布函數由它們的邊緣分布函數生成的變化特性。許多實際應用中經常關心隨機變量的壽命問題，如在可靠性理論中討論了串聯系統的壽命，而且為了方便引入了可靠度函數R（x）=P（X≥x）==1-F（x），對于具有聯合分布函數 H（x，y）的二維隨機變量（X，Y）也有可靠度函數R（x，y）=P（X≥x，Y≥y），Nelsen 等人提出與之對應的生存Copula——（u，ν）=u+ν-1+C（1-u，1-ν），C（1-u，1-ν）表示 P（X≥x，Y≥y）。

研究兩個隨機變量的相依性是Copula的一個重要應用，l966年Lehmann引出了正相依和負相依的概念[3]。設X1，…，Xn是具有聯合分布函數H（x1，…，xn）的隨機變量，且分別有連續的邊緣分布F1，…，Fn以及 Copula，若對所有的 Rn中的（x1，…，xn），有 H（x1，…，xn）≥F（x1）F（x2）…F（xn），則 X1，X2，…，Xn是正相依的，簡記為 PDQ（X，Y）。

在可靠性理論中，對系統壽命的研究只限于各個部件獨立的情況，在本文中將討論部件之間不相互獨立的時候系統的可靠度，把系統壽命的問題和Copula函數聯系了起來，通過Copula的性質來探討系統壽命的一些變化[4]。

2 部件相依的串聯系統可靠性分析

機械系統中，可靠度函數的隨機變量常常具有真實的物理意義，如：時間、循環數、行駛里程等。為便于表述，本文在分析中統稱為壽命。

設某裝備由n個構件組成，構件的壽命是隨機變量 T=（T1，T2，…，Tn），具有聯合分布函數為 H（t）=P（T1＜t，T2＜t，…，Tn＜t），且分別具有邊緣分布函數（即失效函數，可由試驗獲取）為Fi（t），i=1，…，n，Copula函數為C，生存Copula函數為C^，則可得

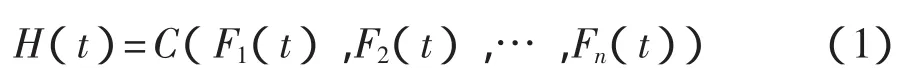
各構件的可靠度函數為Ri（t）=1-Fi（t），系統的可靠度函數為 R（t）。

2.1 串聯系統

系統中只要有一個構件發生故障，系統就發生故障，這種系統稱為串聯系統。串聯系統的可靠性框圖如圖1所示。

圖1 串聯系統可靠性框圖

系統各構件串聯時，系統的壽命為各構件中壽命最小的，即 T=min（T1，T2，…，Tn），則系統的可靠度可表示為

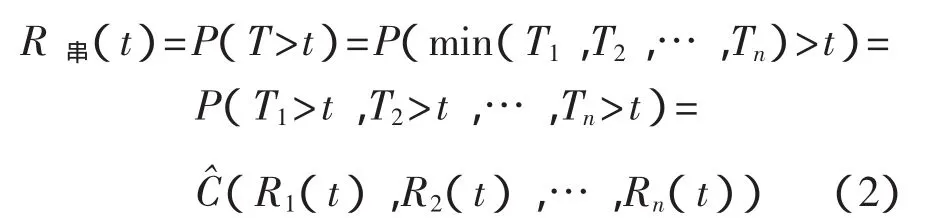
式（2）表示系統可靠度可由生存Copula函數求出。需要說明的是，對于多維的情況，生存CopulaC^不一定是Copula函數。

（1）當各構件獨立時，根據隨機變量獨立的性質

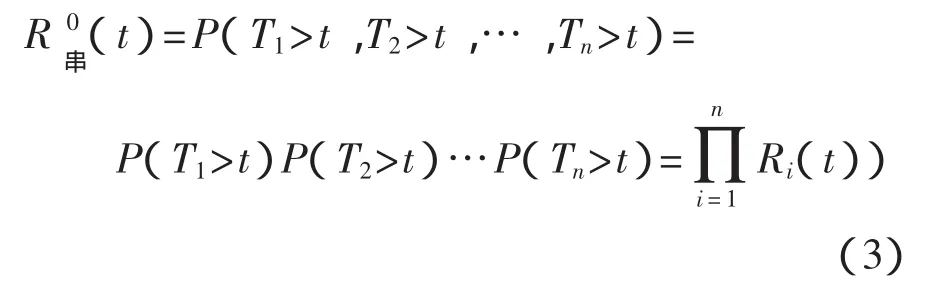
即各構件獨立系統的可靠度等于系統中所有構件可靠度的乘積[5]。

（2）當各構件完全相關時，根據最薄弱環節理論，即認為構件可靠度函數是完全相關的兩兩線性關系此時系統可靠度等于系統中可靠度最小的構件的可靠度[6]。

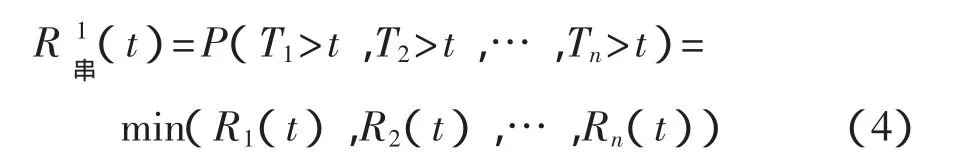
（3）當各構件部分相關時，根據論文對生存Copula C^的介紹，可以通過構造函數找到滿足Copula函數定義的C^，該方法簡單易用，是計算時的首選，但是在構造Copula函數時會受到一定限制。作為一般情況，下面給出2種通用方法。

1）根據串聯系統的定義可知，系統中任意一個構件失效系統就失效，即系統的失效率相當于各構件發生失效事件的集合的并集，因此可以把式（2）做如下變換

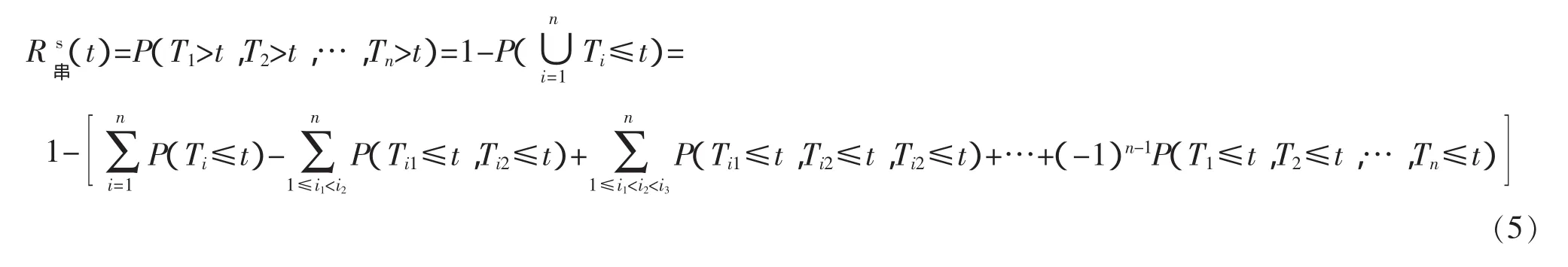
根據 Copula 函數的性質：C（1，…，1，ui，1，…，1）=ui，式（5）變為

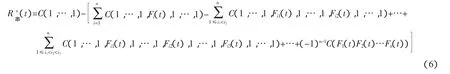
當系統構件較多，即維數n較大時，式（6）中的Copula函數C構成復雜，編程難度和計算量較大，為解決該問題，本文采用下述方法處理高維問題。

2）如圖1所示，首先把構件1、2作為一個子系統，求該子系統的可靠度函數，然后該子系統與構件3組成一個子系統，求該子系統的可靠度函數，如此循環求解直至得到可靠度函數

步驟如下

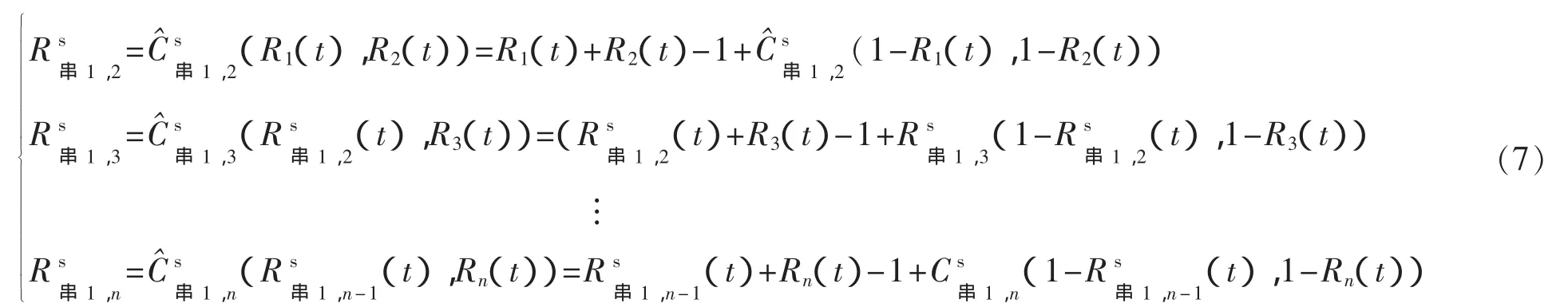
該方法在計算中始終只處理二維問題，C與C^的關系可由式（2）表示，計算量小、便于編程，但是運算過程中各步出現的Copula函數不相同，考慮到簡化計算，可以把整體Copula函數的二維形式作為統一的Copula函數進行運算。

（4）串聯系統可靠度的界

即各構件完全相關時的可靠度大于各構件獨立時的系統可靠度。

在機械系統中，由于各構件之間承受共同載荷沖擊、共同的外部工作環境等原因，多表現為正相關性，即在一定應力作用下，一個構件的強度會隨著另一構件強度的衰減而衰減[8]。當各構件完全相關時，系統具有最高的一致性；當各構件獨立時，系統具有最大的隨機性。對于串聯系統而言，一致性好對系統有利，因此當各構件完全相關時可靠度最大，當各構件獨立時可靠度最小，則式（8）成立

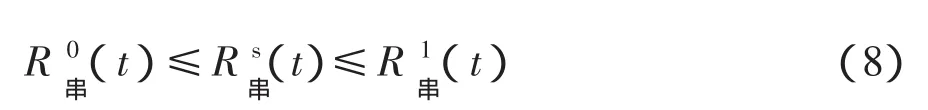
2.2 計算分析

某型車輛行走系統的扭力軸系統由12根扭力軸組成，對整個車輛系統起到支撐和減震的作用，該系統是12維的串聯系統。

在行駛過程中，每根扭力軸依次駛過相同的路面，由于車輛對松軟地面的壓實作用及車輛前部對所受沖擊的吸收作用，各扭力軸的行駛工況表現為近似相同，但工況分布又呈現出從前至后惡劣程度逐漸減弱的特點，也就是說各扭力軸表現為部分相關。

在G級路面2擋車速工況下，單個扭力軸的可靠度函數為

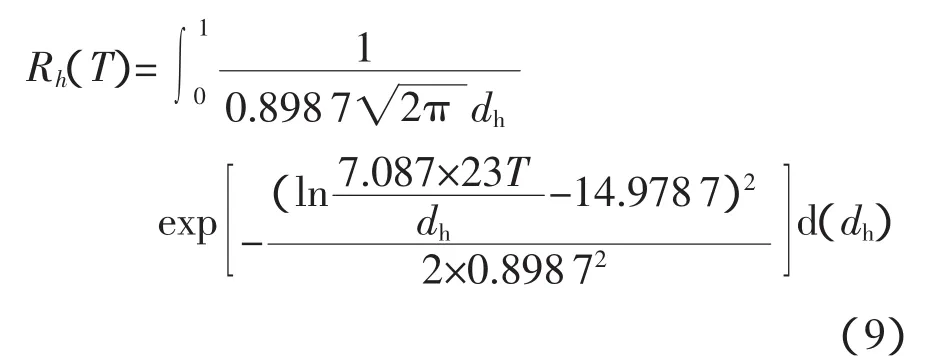
Gumbel Copula函數廣泛應用于多元聯合生存函數的構造問題，由于生存函數和可靠度函數在數學上具有一致性，因而這類分布同樣也適用于聯合可靠度函數的構造。且該Copula族屬于Archimedean Copula的范疇，構造簡單；因此，選取Gumbel Copula函數作為可靠度Copula函數，Gumbel Copula聯合分布函數的表達式為

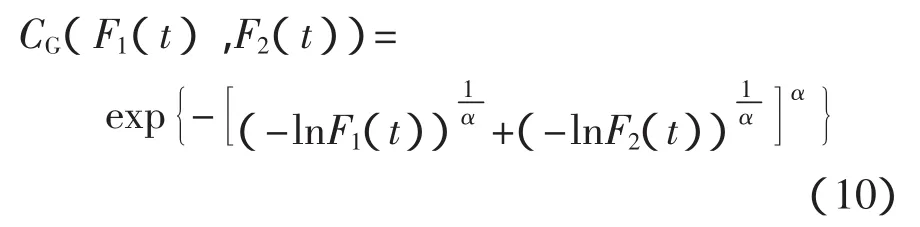
式中：α∈（0，1]。

可以驗證，當α=1時隨機變量獨立，當α減小時隨機變量的相關性加強，當α→0時，隨機變量趨向于完全相關。參數α可以由極大似然法進行估計。但是由于扭力軸的試驗數據較少，因此論文參考其他機械可靠性的數據給出α=0.2的估計值。

根據串聯系統可靠度的第2）種算法，經編程，扭力軸系統在G級路面2擋車速工況下的行駛里程與存活概率的關系圖如圖2所示。

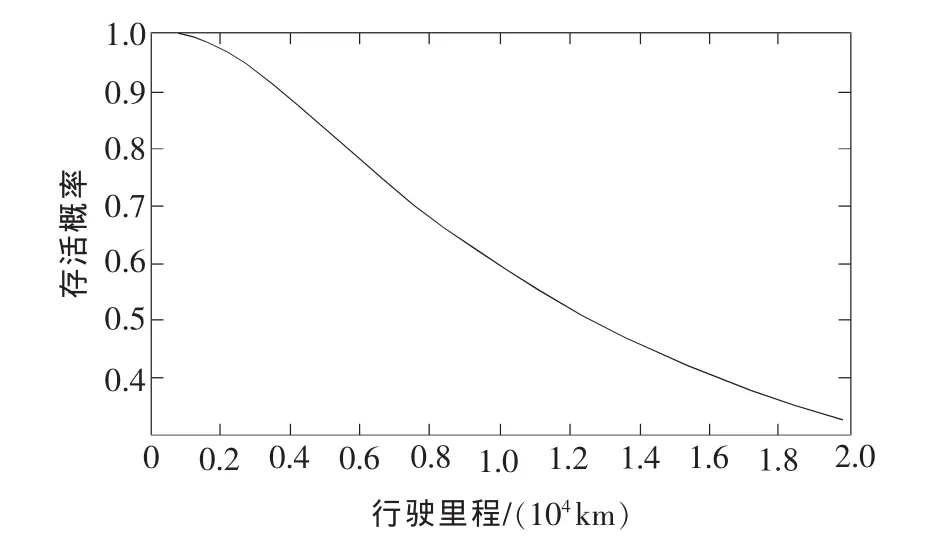
圖2 G級路面2擋工況扭力軸系統行駛里程與存活概率的關系圖

從圖2可以得到，自行火炮在G級路面2擋車速工況下，存活概率等于99%時，扭力軸系統可以行駛1 470 km；當存活概率為90%時，可以行駛3 745km。可見由于各扭力軸之間具有一定的相關性，采用獨立性假設計算系統可靠度會造成比較大的誤差。

3 結束語

本文介紹了Copula函數的定義和相關性質，并給出了由Copula函數來構造多隨機變量聯合分布函數的方法。基于該理論對串聯系統進行了詳細的分析，提出一種計算部件相關的串聯系統的系統可靠性方法。該方法考慮了系統中各部件的相關性，使得系統可靠度的計算結果更為合理，為評估裝備系統的可靠性提供了一種新方法。

[1]Freuent A M.The safety of structures[J].ASCE Trans.1947（112）：125-129.

[2]Wirsching P H.Probability-based fatigue design criteria for offshore structures[R].1983，65（4）：42-55.

[3]Martindale S G，Wirsching P H.Reliability-based progressive fatigue collapse[J].Structural Engineering，ASCE，1983，109（8）：1792-1811.

[4]Neslen R B.An Introduction to Copulas[C]∥New York:Springer-Verlag，1999（97）：145-148.

[5]Benesty J.The committee on fatigue and fracture reliability of the committee on structural safety and reliability of the structural division fatigue reliability[J].Journal of the Structural Division，1982，108（1）：3-88.

[6]張明珠.基于Copula函數對相依部件系統可靠度的度量和改進[J].許昌學院學報，2005，24（2）：14-17.

[7]董聰，楊慶雄.結構系統疲勞壽命可靠性分析理論與算法[J].航空學報，1993，14（5）：247-253.

[8]陳伯真，胡毓仁，顧劍民.結構系統疲勞可靠性分析研究評述[J].力學進展，1996，26（4）：500-509.