蜂窩板結構等效彈性模量的測試

郝鴻雁，黃志亮

（1.浙江海洋學院機電工程學院，浙江 舟山 316000；2.三一集團有限公司研究總院，湖南 長沙 410100）

0 引 言

由于蜂窩板具有重量輕、強度高、剛性大、穩定性好、隔熱隔聲等優點，現已廣泛應用在航空航天、機車、船舶、汽車和建筑等領域[1-3]。蜂窩板結構的靜、動力學分析計算成為現階段力學領域研究的一大熱點。以往的研究大多數采用數值解析法進行分析，但其不適用于復雜的蜂窩板結構，利用ANSYS等通用有限元軟件對蜂窩板結構進行力學分析時，由于沒有蜂窩結構單元，使得計算只能采用等效的方式進行。蜂窩板的等效參數可以通過理論方法[4]或實驗方法確定。

理論方法確定等效彈性模量計算過程比較復雜，文獻[5]采用三點彎曲線載荷兩端簡支板的撓度測試方法，得到蜂窩板的等效彈性模量。這種方法后續的計算過程相當繁瑣，并且它是一種靜態的方法。本文提出利用動力學的方法來測試蜂窩板的等效彈性模量的新方法。采用LMS Test.lab聲振試驗系統對某型蜂窩板結構樣件進行模態試驗，獲取了結構的固有頻率和振型。用ANSYS Workbench有限元軟件對試驗結果進行調參，尋求結構的等效彈性模量。

1 蜂窩板結構樣件模態試驗

試驗模態分析是一種系統辨識的方法，是在滿足實際結構可以運用“模態模型”來描述其動態特性的條件下，通過對振動響應數據的處理和分析，尋求其模態參數，包括頻率、阻尼和模態振型[6]。

實際工程中，需根據實驗目的選擇不同的模態參數估計方法。多參考點最小二乘復頻域法（PolyMAX）是比利時LMS公司開發的一種全新的模態參數頻域識別方法[7]。PolyMAX法既適用于弱阻尼也適用于強阻尼密集模態系統，即便是未得到充分激勵的模態也能良好的識別出來。

PolyMAX法是以頻響函數矩陣H作為擬合函數，H的頻域矩陣分式表達為

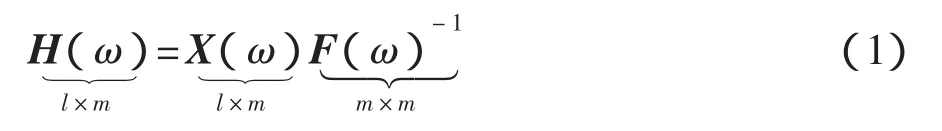
式中：m——輸入（激勵）參考通道總數；

l——輸出（響應）通道總數。

將分子、分母定義成多項式的形式為

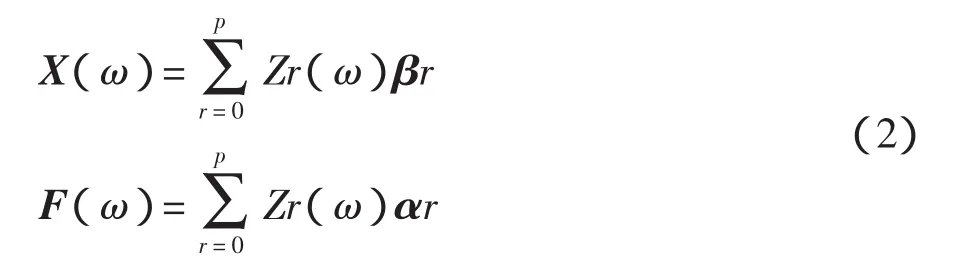
式中：Zr（ω）——多項式基本項，表達式為=e-jωΔt；

βr——l×m階分子多項式系數矩陣；

αr——m×m階分母多項式系數矩陣；

p——數學模型設定的階次；

Δt——采樣時間。

將式（2）代入式（1）得到的頻響函數矩陣為

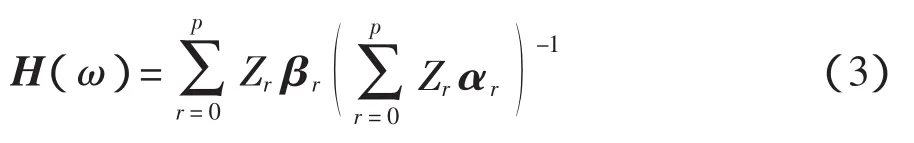
在PolyMAX法中一般設定αr、βr中的元素均為實值系數，于是可表示為

對于頻響函數FRF數據頻率軸上任意頻率ωk，由實測頻響函數可以列出式（3），取不同的頻率列出足夠數量的方程。最后利用最小二乘法估計便可求得待定的分子和分母多項式系數矩陣βr、αr（r=0，1，…，p），通常取 αp=Ⅰ。

在求得分母多項式系數矩陣αr的基礎上，將其擴展成友矩陣的形式；再對友矩陣進行特征值分解，就能得出系統的極點和模態參與因子

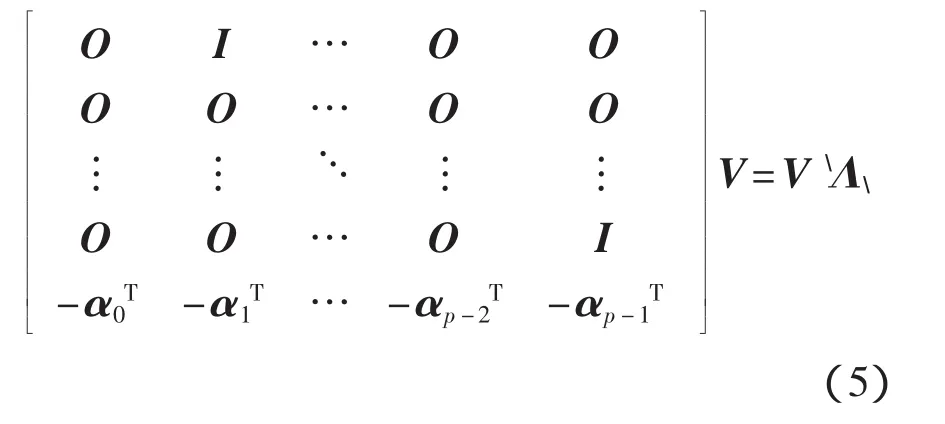
其中，Λ為友矩陣的特征值矩陣（對角陣），其對角線元素（特征值）為λi=e-piΔt（i=1，2，…，mp），它們總是以共軛復數形式成對出現的，且

由特征值分解得到的特征向量 V（mp×mp），取其最下面m行構成的矩陣即為模態參與因子矩陣L（m×mp）；其每一列向量li代表各個輸入對相應模態的比例貢獻。

PolyMAX法采用一種比較簡便的方法，即采用最小二乘頻域法（LSFD）求模態振型，其擬合函數為

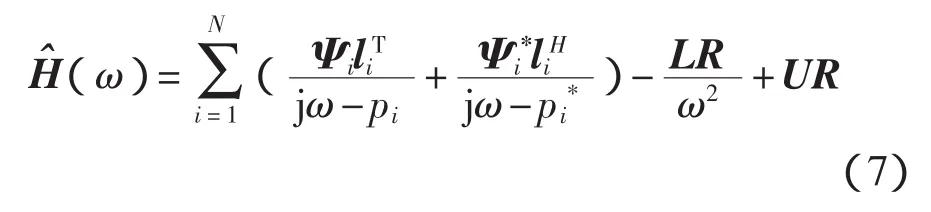
Ψi（l×1）——待求的第i階模態振型列向量；

liT（1×m）——模態參與因子行向量；

liH（1×m）——li的共軛轉置；

LR、UR（l×m）——分析頻帶有外模態影響的下殘余項和上殘余項。

由于極點pi和模態參與因子向量都已求得，于是可由測量的頻響函數（ω）按不同頻率列出式（7），然后用線性最小二乘法求出式中未知的模態振型Ψi以及上、下殘余項LR、UR。

1.1 模態試驗方法及其測試系統

本實驗利用多點激勵單點拾振的方法對蜂窩板在自由約束狀態下進行模態試驗分析。實驗使用300mm×300mm×3mm、345g的蜂窩板樣件，總計布置了36個測點，試驗模型及測點布置如圖1所示。實驗中將蜂窩板4個角用軟海綿墊支撐以模擬其自由約束狀態。

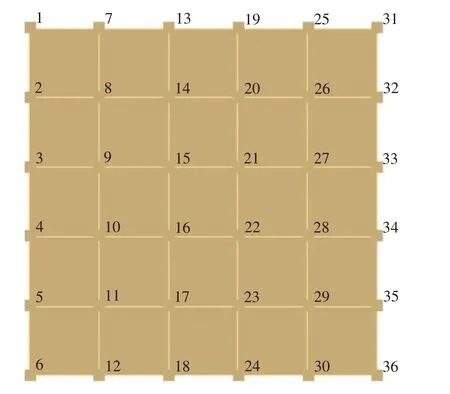
圖1 蜂窩板試驗樣件幾何測點布置

在LMS Test.lab聲振試驗系統中，利用錘擊法對蜂窩板試驗樣件進行了實驗模態分析。模態試驗測試系統框圖見圖2。

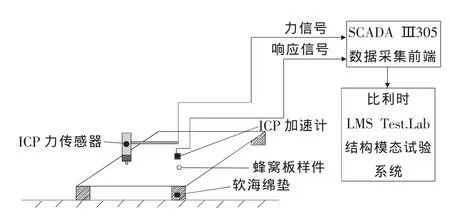
圖2 基于LMS Test.lab蜂窩板結構模態試驗系統框圖

模態試驗時，將一個PCB 333B30單向加速度傳感器（質量約為4g）固定于10#測點，移動脈沖錘依次進行頻響函數的測量。根據板殼振動理論[8]可知，其相對質量ζ近似等于零；因此，附加傳感器的質量對模態試驗結果的影響可以忽略不計。

式中：m——附加質量；

M——板的質量。

1.2 模態試驗結果

采用PolyMAX模態參數識別法[7]對頻響函數從100～400Hz進行模態分析，得到的穩定性分析圖如圖3所示。

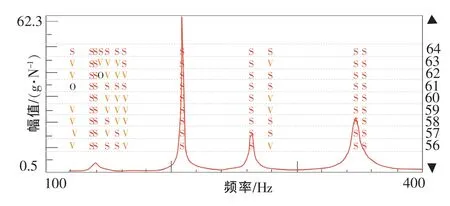
圖3 PolyMAX法模態穩定性圖

從圖3中可以看出：有模態的位置出現一系列s標識，這說明利用PolyMAX法分析得到的頻率、阻尼和模態參與因子全部穩定。

采用PolyMAX法識別出來的蜂窩板樣件模態參數見表1。自由約束狀態下的模態振型如圖4所示。

表1 自由約束狀態下蜂窩板試驗樣件模態試驗結果

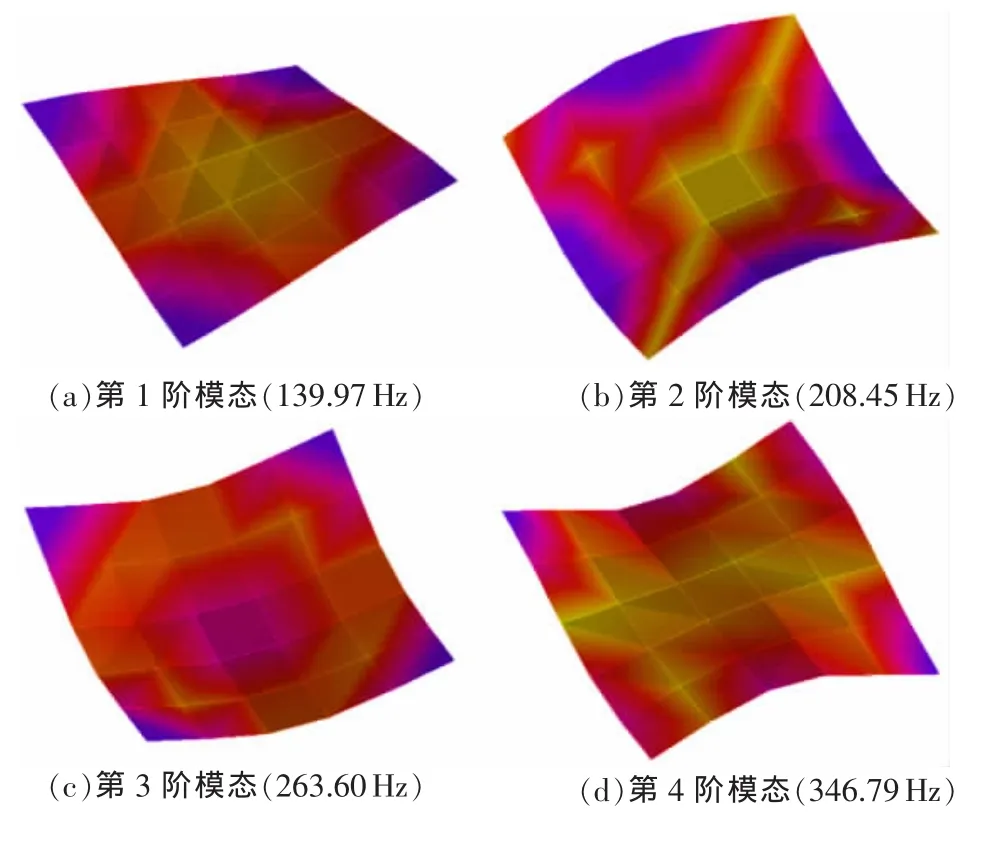
圖4 蜂窩板試驗樣件前4階模態振型

模態試驗完成后，為防止引入虛假模態和丟失真實模態，需要對模態進行驗證。而模態判定準則（modal assurance criteria，MAC）不僅可以檢驗模態的真實性，更廣義地說它是衡量模態有效性的尺度。其中模態判定準則通過比較不同模態向量間的線性相關性來判斷各階模態的置信度。在工程分析中，兩個模態振型向量Ψi和Ψs之間的模態判定準則定義為

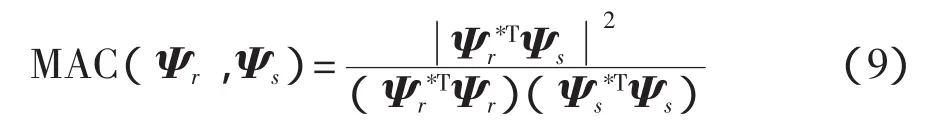
MAC取值從0到100%。若MAC取值越接近100%，則兩個模態振型向量是同一個物理振型的估計；若兩個模態振型向量是不同物理振型的估計，則MAC取值應該接近0。即取值為100%說明兩者是同一物理振型且具有一致的相關性，同時也說明了模態參與因子的有效性；反之，若MAC取值為0，則說明兩個模態振型向量是不同的物理振型且沒有一致的相關關系，它們是相互獨立的。

從模態置信分析圖5中可以看出，由PolyMAX模態參數識別法識別出的蜂窩板各階模態之間滿足模態正交性原理；同一物理振型具有比較好的一致性，不同物理振型基本上是相互獨立的。因此，本次模態試驗所得到的蜂窩板結構模態真實可靠，不存在虛假模態。

2 蜂窩板等效彈性模量的確定

2.1 蜂窩板的等效方法

本文試驗的蜂窩板是在假定空間體積和厚度不變的情況下，將其等效成一個等厚度的實心板。等效實心板的密度就可以由蜂窩板試驗樣件的重量除以實心板的體積得到。

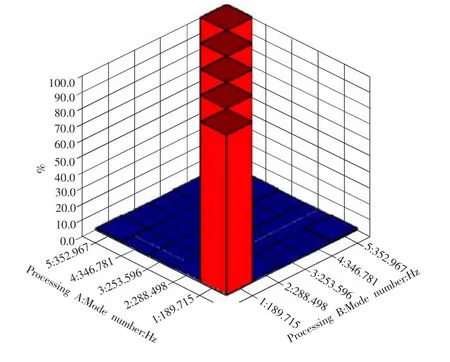
圖5 蜂窩板結構模態置信分析圖

式中：M——板的質量；

V——板的空間體積。

通過計算蜂窩板等效密度ρ=1278.11kg/m3。

2.2 基于ANSYS Workbench調參確定等效彈性模量

經過多次調參試湊，使有限元分析得到的固有頻率和振型與實驗結果趨于一致，從而得到蜂窩板等效模型彈性模量的確定值E=55GPa。

在等效彈性模量E=55GPa的情況下，蜂窩板等效模型結構模態有限元分析結果見表2，前4階模態振型如圖6所示。

通過對比蜂窩板等效模型模態有限元分析結果與實驗結果可以看出，各階模態振型非常一致，模態振型分別為：第1階模態為對邊節線四角局部振動，第2階模態為對角節線四邊局部振動，第3階模態為環形節線局部振動，第4階模態為對邊1節線和對邊2節線局部振動；且各階模態振型對應固有頻率非常接近，誤差在5%以內。說明通過試驗調參得到的蜂窩板結構的等效彈性模量，在動力學仿真分析中能夠準確反映蜂窩板實際結構的動態特性。

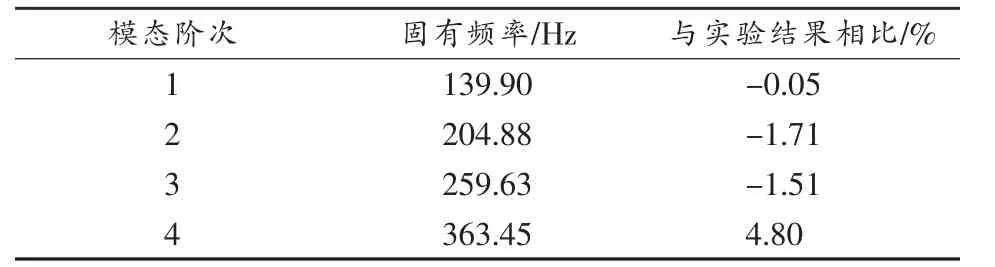
表2 自由約束狀態下蜂窩板等效模型模態有限元分析結果

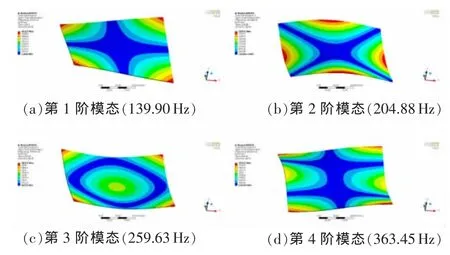
圖6 蜂窩板等效模型前4階模態振型

3 結束語

本文所采用的蜂窩板等效模型以及調參確定的等效彈性模量，在動力學分析時能夠真實反映蜂窩板實際結構的動態特性。在等厚度等效方法的情況下，所確定的等效彈性模量真實可靠。同時該等效模型及其等效彈性模量也適用于靜力的有限元分析。

[1]彭明軍，孫勇，沈黎，等.面板對釬焊蜂窩鋁板平壓性能的影響[J].材料導報，2006，20（7）：471-472.

[2]迎春.鎂合金蜂窩板的制備及力學性能研究[D].大連：大連交通大學，2009.

[3]付立英，王維揚.衛星用蜂窩夾層板的等效計算及實驗研究[J].科學技術與工程，2008，8（27）：6429-6432.

[4]陳昌亞，王德禹，王本利.動力學分析中鋁蜂窩夾層板的等效問題[J].空間科學學報，2002，22（增刊 2）：142-148.

[5]程軍，曾偉明，方如華，等.金屬蜂窩夾芯板等效彈性模量的實驗測試[J].實驗力學，2003，18（1）：50-55.

[6]Ward H，Stefan L，Paul S.Modal analysis theory and testing[M].Leuven Belgium Department of Mechanical Engineering，Katholieke Universiteit，1995：80-99.

[7]劉馥清，安宏偉.多參考最小二乘復頻域（PolyMax）法在汽車輪胎及車身模態參數識別中的應用 [C]∥2006LMS首屆用戶大會論文集.蘇州：2006：1-7.

[8]曹志遠.板殼振動理論[M].北京：中國鐵道出版社，1983：59-67.