基于圖嵌入的特征提取算法研究
王化喆,劉 佳,,王 勝
(1.商丘職業技術學院,河南 商丘 476000;2.南京理工大學,江蘇 南京 210000)
1 圖的定義
一個圖G就是一個有序的三元組(V(G),E(G),ΨG),其中V(G)是非空的頂點集,內部元素稱為圖G的頂點,E(G)是不相交的邊集,內部的元素稱為圖G的邊.ΨG稱為關聯函數,它使G的每條邊對應于G的無序頂點對.如圖1所示:
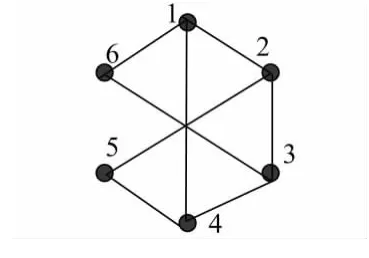
圖1 圖G的結構
2 圖嵌入
G={X,W}是一個圖,其中X為頂點集,W 為相似度矩陣,W ∈RN×N.Wij度量數據點Xi與Xj的相似度,如果Wij=0就認為點xi,xj的相似度為0.W 可以依據不同的準則來定義.圖G的對角矩陣D和拉普拉斯(Laplacian)矩陣L定義如下:

該文的圖嵌入定義如下:
設向量x∈RD,y∈Rd,(d?D),x→y,并且數據集Y能夠很好地保持原來數據集X相似關系(即圖G).假設數據集X的本質圖為G,懲罰圖為Gp.圖結構保持準則定義如下:

其中L定義如公式(1),限制條件yTBy=d用來獲得最優的數據.
B的定義如下:若只有本質圖時B=D,此時B作為一個圖歸一化矩陣;當有懲罰圖時B=LP=DPWP,DP定義如公式(2),此時B作為一個懲罰項.圖結構保持含義如下:原始數據相似度較小的點相似度變小,原始數據相似度較高的點映射之后相似度變大.
由于上述圖結構保持準則只計算出訓練樣本的低維嵌入,而不是全體樣本的.因此,下面介紹一種線性化的嵌入映射[1]2323-2325.
設向量x∈RD,y∈Rd,(d?D),x→y=,P為映射變換向量。此時公式(2)可變化為下式:
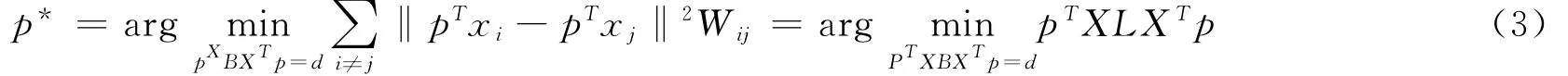
歸一化后的映射變換向量P,即為映射變換的方向。可以通過核化來計算非線性映射變換向量,通過張量化來計算映射變換矩陣.
3 基于圖嵌入的算法分析
3.1 主成分分析
主成分分析(Principal Components Analysis,PCA),本質上是數學統計的特征分析算法,基于PCA算法抽取出的人臉特征——特征臉.基于特征臉的人臉識別算法是較為經典的識別算法之一,成為鑒別新算法優劣的基準算法之一[2]40.其基本原理如下:
設樣本數據集X = (x1,x2,…,xN),其中xi∈RD,i=1,2,…,N.樣本xi的類別標簽為ci∈ {1,2,…,Nc},其中Nc為樣本數據集類別數,第i類的樣本的總數為ni.PCA尋找最優的映射變換矩陣P,將iD空間的數據映射到一個相對低維的特征空間id((d?D))中.
樣本數據集的平均值為:

則其協方差矩陣如下:

其目標函數為:
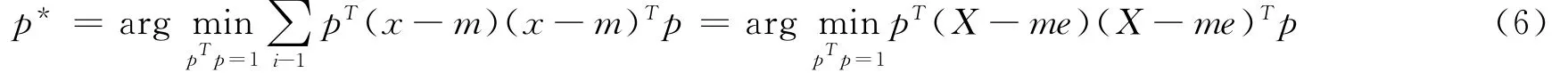
協方差矩陣可以推導如下:

3.2 線性鑒別分析
線性鑒別分析(LDA)的主要思想是:計算使得Fisher準則函數得到最大值的向量作為映射向量.即使類間散度矩陣和類內散度矩陣之商獲得最大值的向量,因此該向量可以通過計算類間散度矩陣和類內散度矩陣的廣義特征向量獲得.
最佳鑒別矢量投影矩陣的計算,利用矩陣論相關知識使該投影矩陣投影后保證有最大類間距和最小類內距,即具有最大的可分離性[3]67.因此,它是一種有效的特征抽取方法.其基本原理如下:
設樣本數據集X = (x1,x2,…,xN),其中xi∈RD,i=1,2,…,N.樣本xi的類別標簽為ci∈ {1,2,…,Nc},其中Nc為樣本數據集類別數,第i類的樣本的總數為ni.LDA尋找最優的映射變換矩陣P,將iD空間的數據映射到一個相對低維的特征空間id(d?D)中[4]100.令映射函數為:

i類樣本均值計算如下:

總體樣本均值:

根據類間離散度矩陣和類內離散度矩陣定義,可以得到如下式子:
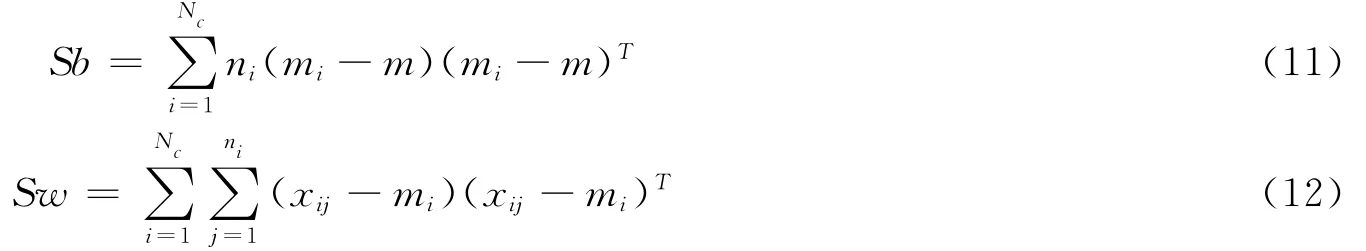
與LDA類似,MFA的目標函數如下:

類間離散度矩陣可以變換為:

類內離散度矩陣可以變換為:
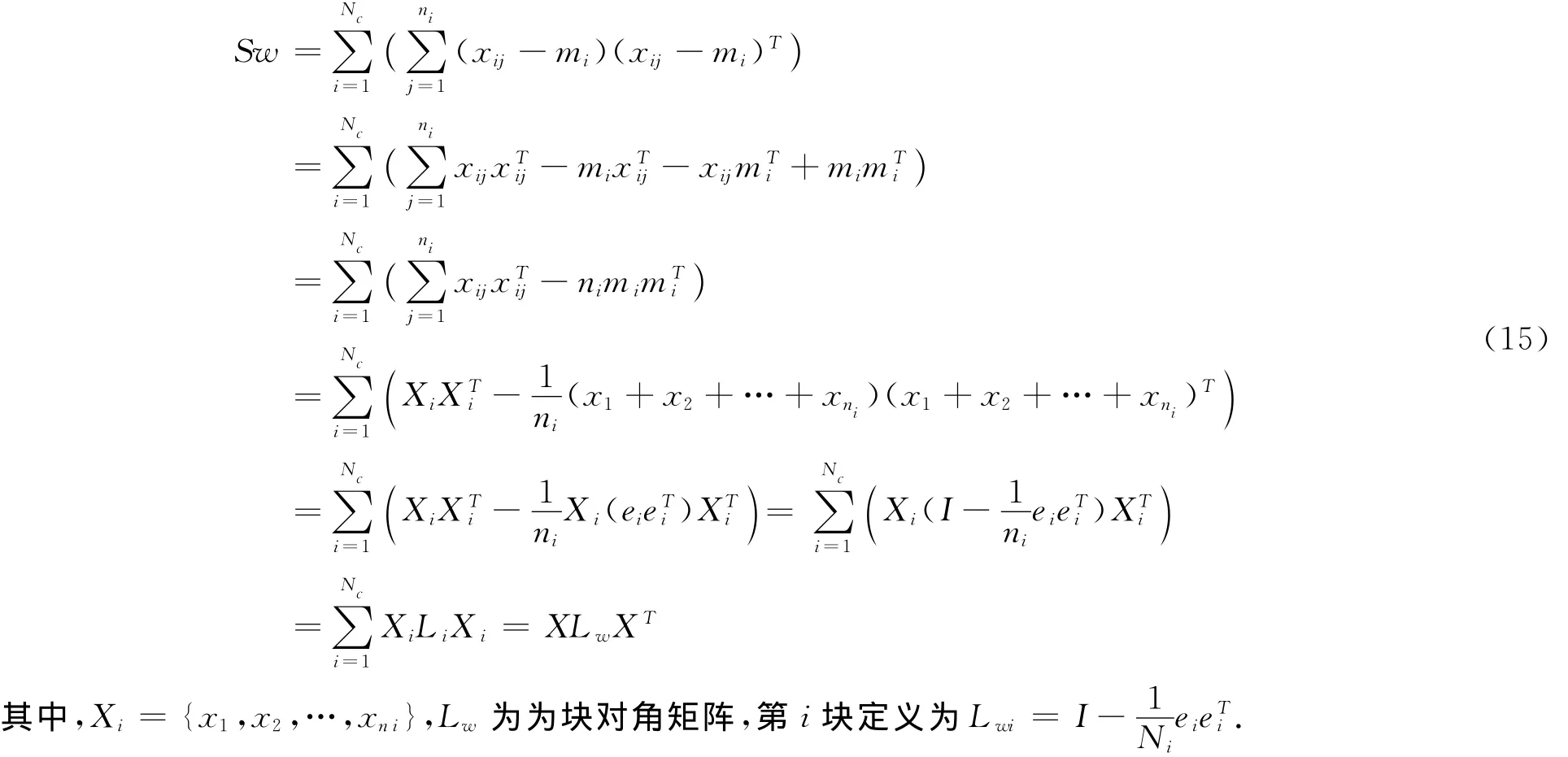
故LDA的目標函數可以變換為:
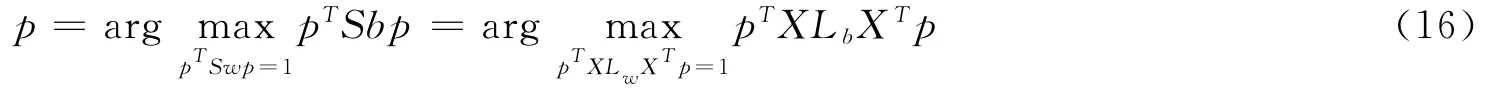
由公式(16)可以看出LDA也可以看做一種圖嵌入.
3.3 L1圖及其嵌入
設數據集X= (x1,x2,…,xN),其中xi∈RD,i=1,2,…,N..L1圖的目的是利用訓練樣本表示每一個訓練樣本,同時要求用來表示每一個測試樣本的訓練樣本盡可能的稀疏.
L1計算方法如下:

其中ai∈RN-1;
利用NPE類似的方法可以實現L1圖的嵌入。同時,嵌入映射變換矩陣P可以通過計算下面最小化問題得到:
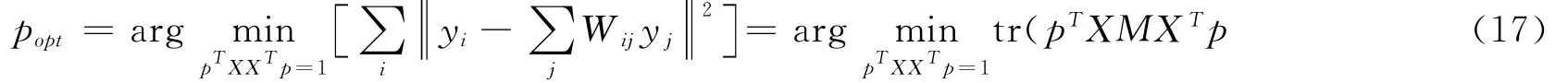
約束條件為PTXXTP=1.其中tr表示矩陣的跡,M的定義如下:

4 結論
通過對PCA,LDA,L1等經典算法的代數推導及對比可以得出,這些經典算法都可以利用圖嵌入框架理論來解釋并統一到此種框架中.由此,得出特征提取算法的核心是樣本的圖構造,對于降低特征提取算法的計算復雜度和提高算法的效率有較好的效果[5]189-201.
[1]T.Roweis,L.K.Saul.Nonlinear Dimensionality Reduction by Loeally Linear Embedding[J].Seienee,2000,290(5500).
[2]C.Yan,D.Xu,B.Y.Zhang.Graph embedding andextensions:ageneral framework for dimensional-ity reduetion.IEEE Tran[J].s.on Pattern Analysis and Maehine Intelligenc,2007,29(1).
[3]黃 鴻.圖嵌入框架下流形學習理論及應用研究[D].重慶:重慶大學,2008.
[4]邊肇棋,張學工.模式識別(第二版)[M].北京:清華大學出版社,2000.
[5]X.F.He,D.Cai.Learning a Maximum Margin SubsPa-ce for Image Retrieval[J].IEEE Trans.on Knowledge and Data Engineering,2008,20(2).

