PCA算法和數學形態學理論在踝臂指數測量中的應用

戶鵬飛，遲鶴翔，劉寶華，2

（1．燕山大學河北省并聯機器人與機電系統實驗室，河北秦皇島 066004;2．北京航空航天大學自動化科學與電氣工程學院，北京 100191）

0 引言

踝臂指數（ankle-brachial index，ABI）是踝部動脈收縮壓與雙側肱動脈收縮壓的最高值之比，它是診斷外周動脈疾病（peripheral artery disease，PAD）的一種簡便、無創的方法［1］。因此，測量ABI的關鍵在于準確測量出上肢和下肢的動脈收縮壓。目前，測量動脈收縮壓的主要方法是雙層袖帶測量法，使用該方法可以準確測量出上肢肱動脈收縮壓。但是人體下肢有多條動脈，而且前脛骨動脈和腓骨動脈在脛骨和腓骨之間，導致無法利用袖帶加壓來完全阻斷這2條動脈的血液流動。所以，即使在很高的壓力下仍然可以監測到幅值很高的脈搏波波動［2］。此時檢測到的信號會是多條血管的脈搏波疊加后的波形，在疊加后的脈搏波波形圖中，用直觀的方法很難分辨出重新恢復血液流動時的第一個脈搏波，所以，在下肢的收縮壓測量中準確地識別脈搏波重新恢復波動的起點成為關鍵。

為了準確找到下肢脈搏波重新恢復波動的起點，本文利用主成分分析（PCA）算法，將采集的脈搏波信號進行分離，從而找到被加壓袖帶阻斷的血管的脈搏波信息，并用基于數學形態學的梯度原理來處理分離后的脈搏波，從而成功找到脈搏波重新恢復波動的起點，為準確測量ABI提供依據。

1 PCA

1．1 動態嵌入

為了應用PCA分離采集到的脈搏波，需要多維脈搏波數據，但受袖帶體積和人體小腿尺寸以及實際的需要，必須減少傳感器數量。因此，實際檢測過程中只能用一維信號進行分離，這樣的分離系統屬于欠定系統。參照參考文獻［2］應用的動態嵌入 （dynamical embedding，DE）技術構建采樣時間序列，盡可能不失真地還原脈搏波信號。

DE即通過對觀察得到的連續時間矢量進行延遲，得到新的狀態空間［2，3］。確定延遲矢量維數后，就可以由大量的連續延遲矢量構建內嵌式矩陣，其表達形式如下

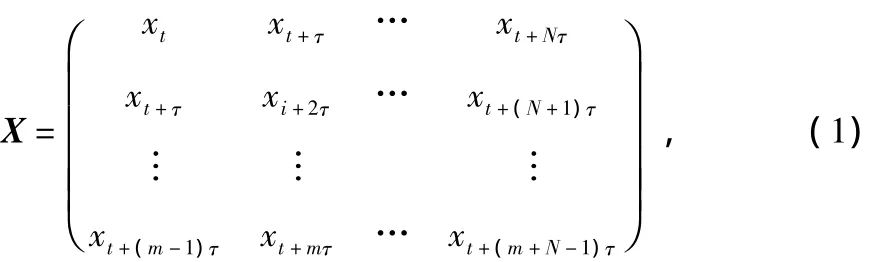
式中N為信號長度，τ為延遲，m為內嵌式矩陣維數。

1．2 PCA

PCA是一種常用的基于變量協方差矩陣對信息進行處理、壓縮、抽提的有效方法。該算法可以用于數據的降維，是一種統計分析技術，其目標是找到數據分布方差最大的方向，并將數據向該方向投影并保持投影后恢復數據的殘差最小。對數據降維時，計算輸入數據向量的相關矩陣Rxx的特征值和特征向量，然后將原始向量投影到m個優勢特征值對應的特征向量空間。

用PCA算法進行信號分離時，假設經動態嵌入后得到的矩陣為X，其協方差矩陣為C。對X進行PCA的過程就是求其協方差矩陣C的特征值λ對應的標準正交特征向量V的過程，即滿足公式

然后，按照特征值的大小對提取出來的主分量進行排列［4］，得到相應的解混信號。

通過袖帶采集的踝部脈搏波數據包含多條動脈信息，人體踝部有4條主動脈。這些動脈血管深淺不一，脈動強度有所不同，故能量也有所差異，適合從能量的角度進行分離。PCA就是從信號的能量角度進行分析，把這些動脈信息分離的過程就是從采集的一維脈搏波信號中進行主分量提取的過程。分離后的脈搏波通過人眼識別可以輕松找到脈搏波恢復跳動的起點，但是對于計算機來說，識別第一個脈搏波的峰值仍然具有一定難度，這就需要將峰值的特征更加顯著化，用數學形態學處理分離后的脈搏波可以達到這個要求。

2 數學形態濾波與波形提取

2．1 數學形態學原理

數學形態學是在集合論和積分幾何的基礎上發展起來的非線性分析方法。它是用一個已有的結構元素去度量被處理信號。結構元素相當于一個“探針”，根據結構元素的不同，可以有效地對信號中所含的信息進行提取。

數學形態學的基本算子主要包括腐蝕運算、膨脹運算，以及以此為基礎構造的開、閉運算等。這些算子的定義如下:

設原始信號f（n）為定義在F=（0，1，2，…，N－1）上的離散函數，定義結構元素g（n）為G=（0，1，2，…，M－1）上的離散函數，且N≥M，則f（n）關于g（n）的腐蝕和膨脹分別定義為

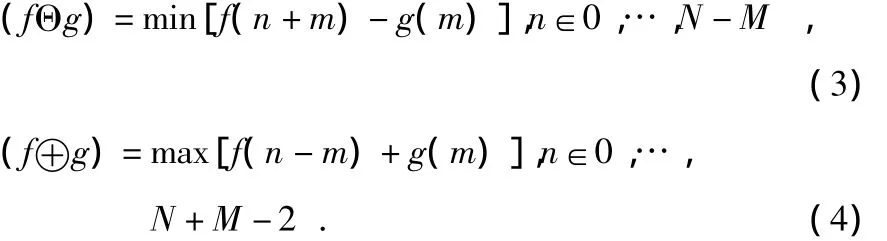
f（n）關于g（n）的開運算和閉運算分別定義為

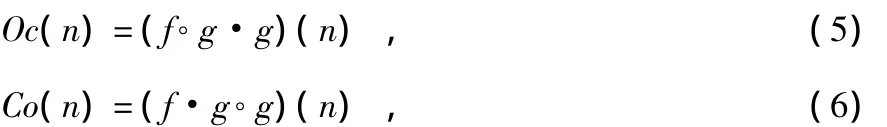
式中 Θ為腐蝕運算，⊕為膨脹運算，?為開運算，·為閉運算［5］。其中，開運算可以抑制信號的正脈沖，即削去信號中比結構元素寬度小的波峰。閉運算可以抑制信號的負脈沖，即填平信號中比結構元素寬度小的波谷。開、閉運算本身和它們的自由組合可以形成不同的形態濾波器。為了同時濾除信號中的正脈沖和負脈沖，通常采用形態開、閉的級聯形式。采用相同尺寸結構元素，通過不同順序級聯開、閉運算定義的形態組合濾波器如下

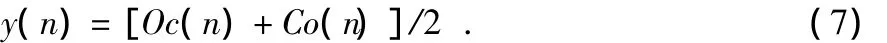
由于開運算的收縮性導致開—閉濾波器的輸出偏小，而閉運算的擴張性導致閉—開濾波器的輸出偏大，因而，存在統計偏倚現象。但是，開—閉和閉—開組合形態濾波器避免了上述缺點，可以使信號盡可能保持其原有幅值和波形［6］。

2．2 數學形態學梯度

f（n）關于g（n）的梯度運算定義為

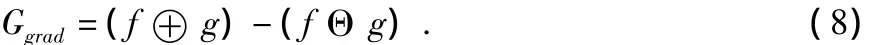
基于扁平結構元素的膨脹和腐蝕運算具有取信號的局部極大和局部極小值的功能，形態學梯度即為二者做差，取局部范圍內的最大與最小值之差，可用于信號的邊緣檢測［7，8］。

數學形態學的各種變換完全是在信號的時域內進行，無關于信號的頻域信息，運算結果只取決于信號的局部形態特征，對局部內信號的變化有較強的識別能力，且運算速度快。對進行ABI測量的脈搏波信號而言，只需要識別其波形，不需要深究其幅值、頻率等信息;在進行ABI測量時，也只需要觀察信號局部的特性——信號各個周期幅值的對比。所以，數學形態學變換適合和PCA算法進行結合，用于ABI的測量。

3 實驗結果與分析

圖1是一組典型的測量ABI時的脈搏波數據。被測者為健康成年人，用雙袖帶方法測得的踝部脈搏波波形。

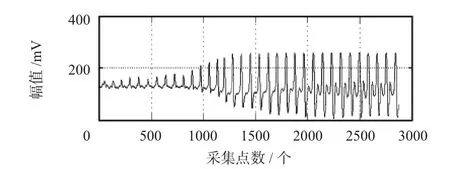
圖1 脈搏波原信號Fig 1 Original signal of pulse wave

對圖1的采樣數據根據動態嵌入技術構建130維內嵌式矩陣，進而用文中提到的PCA分解算法進行解混。解混后的脈搏波波形圖如圖2所示，本文只列出了前6個分量，后面的基本為噪聲信號，不予列出。分析分離后的脈搏波信號，前4個分量能較清晰地辨別出為脈搏波信號，符合人體下肢踝部有4條主動脈的事實，該PCA分離方法為有效分解。

圖2 解混后的脈搏波信號Fig 2 Pulse wave signal after separating

對分離后的脈搏波信號用公式（7）所示的原理進行濾波，濾波時，結構元素寬度的選取對濾波結果有很大影響［9］，這里選擇寬度為8的直線型結構元素。對處理后的動脈脈搏波求其梯度，選取結構寬度為50的直線型結構元素。結果如圖3所示。分析脈搏波信號的梯度圖，在圖上可以清楚地看出:在1000點過后的第2個周期（圓圈標出的位置），脈搏波梯度有一個斜率較大的陡升。該脈搏周期所對應的壓力值即為下肢收縮壓。同分離后的信號波形圖進行比較，梯度圖中波峰更明顯地顯現出來，應用計算機更容易識別到該點峰值，進而選取該時刻的袖帶壓力作為收縮壓進行ABI的計算。一般來說，較淺層的動脈信號易被加壓袖帶阻斷血流，當壓力減小恢復脈搏跳動時，淺層的動脈脈動傳播到傳感袖帶的能量也較大，排序也相對靠前。

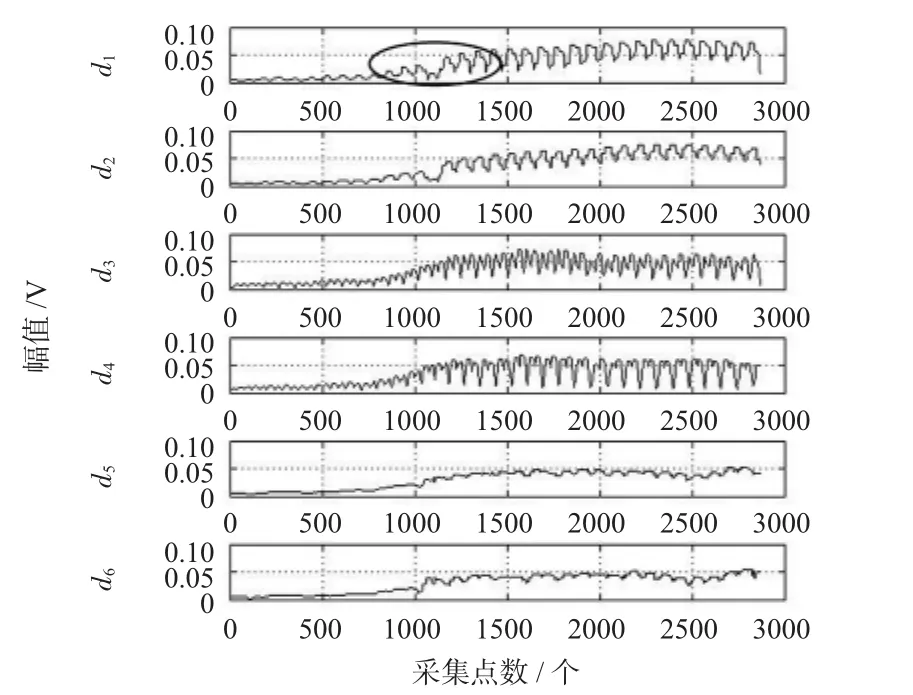
圖3 脈搏波信號梯度圖Fig 3 Gradient figure of pulse wave signal

4 結束語

本文先利用PCA算法對采集的下肢脈搏波信號進行分離，利用基于數學形態的梯度理論對分離后的下肢脈搏波數據進行處理，實驗結果證明:這種方法可以很好地找到下肢動脈在袖帶放氣過程中重新恢復脈搏波動的起點。與傳統的方法相比，這種方法簡單快捷，識別準確，為ABI的準確測量提供了一個新的思路。

［1］ Kenneth O．Peripheral arterial disease［J］．The Lancet，2001，358:1257－1264．

［2］ 劉寶華，戴成武．EVD算法在踝臂指數測量中的應用［J］．傳感技術學報，2010，23（1）:19 －23．

［3］ James C J，Lower D．Extracting multisource brain activity from a single electromagnetic channel［J］．Artificial Intelligence in Medicine，2003，28:89 －104．

［4］ 馬建倉，牛奕龍，陳海洋．盲信號處理［M］．北京:國防工業出版社，2006:36－46．

［5］ 歐陽森．改進數學形態方法及其在電能質量監測中的應用［J］．華南理工大學學報:自然科學版，2005，33（2）:34 －38．

［6］ 李 剛，何宏獻，劉 巍，等．數學形態濾波器及其在心電圖機中的應用［J］．儀器儀表學報，1999，20（4）:335 －339．

［7］ Li B，Zhang P L，Wang Z J，et al．Gear fault detection using multiscale morphological filters［J］．Measurement，2011，44:2078 －2089．

［8］ 鄭 濤，劉萬順，肖仕武，等．一種基于數學形態學提取電流波形特征的變壓器保護新原理［J］．中國電機工程學報，2004，24（7）:18 －24．

［9］ 胡愛軍，孫敬敬，向 玲．振動信號處理中數學形態濾波器頻率響應特性研究［J］．機械工程學報，2012，48（1）:98 －102．