基于EEMD能量熵和LSSVM的傳感器故障診斷*

丁國君，王立德，申 萍，楊 鵬

（北京交通大學電氣工程學院，北京 100044）

0 引言

傳感器在動車組制動控制系統(tǒng)中負責對電壓、電流、速度、壓力和溫度等信號的采集與調理，輸入到制動控制單元進行演算和計算，輸出制動控制力，并根據傳感器信號的變化實時調整制動力的大小，所以，傳感器發(fā)生故障將對動車組的制動性能產生重要影響。傳感器的故障類型主要有偏差故障、沖擊故障、噪聲干擾故障、漂移故障、輸出恒定值故障和周期性干擾故障6種類型［1］。當傳感器發(fā)生故障時，傳感器的輸出信號表現為非線性非平穩(wěn)信號，信號中包含豐富的時域和頻域信息，因此，需要使用時域和頻域相結合的故障特征提取方法才能很好地提取出傳感器的故障信息。

基于信號處理的人工智能方法越來越多地被應用于傳感器的故障特征提取和診斷中，目前應用最廣泛的傳感器故障特征提取方法和故障診斷方法分別是小波分析技術和人工神經網絡［2～4］，但是，小波分析存在低頻區(qū)間分析較粗糙、不會自適應等缺點，人工神經網絡的選擇和容易陷入局部極小點、過學習等問題都是其不容忽視的缺陷。

本文提出了利用集成經驗模態(tài)分解（EEMD）方法對傳感器輸出信號進行若干內稟模態(tài)函數（IMFs）的分解，同時提取不同層次IMFs分量的能量熵作為故障特征向量，這樣既解決了EMD的模態(tài)混疊和端點效應，也解決了小波分析方法在緩變信號的局限性，使傳感器故障特征提取更加準確。同時利用最小二乘支持向量機（LSSVM）的小樣本和風險最小化的特點，能夠迅速地進行故障識別和分類，具有很高的識別精度和速度，對傳感器故障進行診斷。

1 基本原理

1．1EEMD

EEMD方法基于信號的局部特征的時間尺度，克服了EMD方法的端點效應和模態(tài)混疊現象，分解出的各個IMFs突出了數據的局部特征，對其進行分析可以更有效地掌握原始數據的特征信息，每一個IMF都是自適應的，EEMD步驟如下［5，6］:

1）均勻添加白噪聲序列（均值為0，標準差為常數）到目標數據序列上

其中，x（i）為原始信號，n（i）為添加的白噪聲，α為添加白噪聲系數，一般取0．1～0．4之間。

2）將加入了白噪聲序列的數據用常規(guī)的EMD分解為多個IMFs，得到IMF分量cs（i）和余項rs（i）

3）重復迭代步驟（1）和步驟（2），但每次加入的是不同幅值的白噪聲序列。

4）將分解得到的相應IMFs的均值作為最終的分解結果

當N越大，對應的白噪聲的IMFs的和將趨于0，則EEMD的結果為

1．2 LSSVM 原理

SVM克服了神經網絡網絡結構確定困難、收斂于局部極小和不適合小樣本等缺點，有效解決了小樣本、高維數和非線性等學習問題。但在實際應用中，采用逼近算法和多類分類不如兩類分類效果顯著等不足，訓練速度慢，造成SVM泛化能力的下降［7］。

LSSVM 是由 Suykens J A K 和Vandewalle J［8］提出的對SVM的一種改進算法，它用二次損失函數取代SVM中的不敏感損失函數，通過構造損失函數將原SVM中算法的二次尋優(yōu)變?yōu)榍蠼饩€性方程，降低了計算的復雜性，具有更好的抗噪能力和更快的運算速度。

分類問題的目標是求解決策函數y（x）=sgnf（x），其中，函數f（x）形式如下

其中，φ（．）為輸入空間到特征空間的非線性映射，系數向量w和偏差項b為待求量。然后在該映射空間構造分類函數式（6）

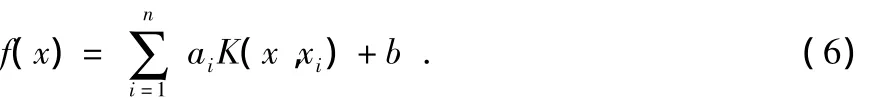
其中，ai為拉格朗日乘子，K（x，xi）為滿足Mercer條件的核函數，b為偏差量。

典型的核函數有多項式核函數、徑向基（radial basis function，RBF）核函數和Sigmoid核函數等。本文采用性能較好的RBF核函數作為LSSVM核函數，其表達式為K（x，xi）=exp（－‖x－xi‖2/σ2），需要優(yōu)化的參數有正規(guī)化參數γ和核函數參數σ2。

2 故障特征提取

由于EEMD的前幾個IMFs分量就包含了原始信號中大部分的信息，而當傳感器發(fā)生故障時，IMFs的能量熵發(fā)生變化，因此，可以從IMFs能量熵入手，通過提取IMFs的能量熵來提取傳感器的故障特征信息，具體的分解步驟如下［9］:

1）對原始信號進行EEMD，選取包含故障主要信息的前n個IMFs分量。

2）求各個內稟模態(tài)函數的能量Ei

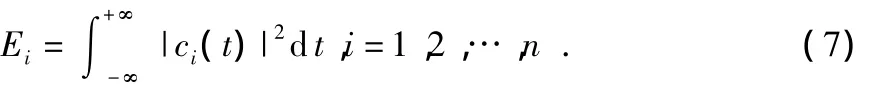
3）所有的IMFs能量熵組成特征向量T

4）為了更好地提取故障特征信息，對每一個IMFs能量熵作歸一化處理

5）可得歸一化處理后的故障特征向量

T'向量可作為LSSVM分類器輸入的故障特征向量。

為了驗證EEMD方法的有效性，對仿真的傳感器的沖擊故障分別利用不同故障特征提取方法提取故障特征，并對比分析。

圖1是仿真的傳感器沖擊故障的輸出電壓信號，圖2是EMD后的沖擊故障的傳感器輸出信號波形，傳感器沖擊故障的輸出信號經過經驗模態(tài)分解后，共分解為8個IMF分量和殘余項，由于沖擊信號是突發(fā)的非線性非平穩(wěn)信號，在EMD分解過程中出現了模態(tài)混疊現象，這影響對傳感器沖擊故障特征的準確提取。

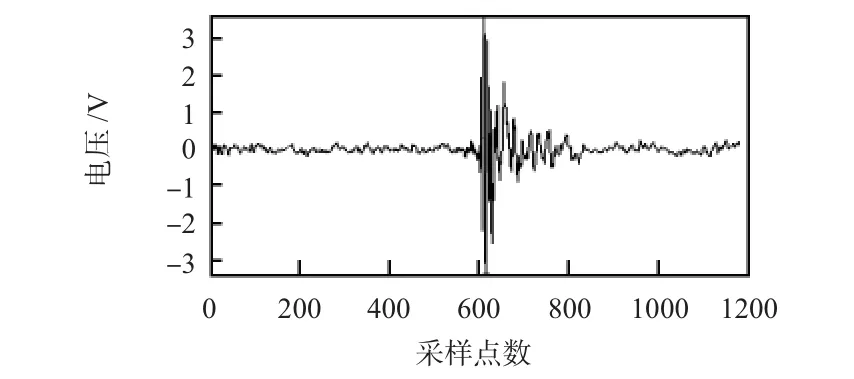
圖1 沖擊故障仿真信號Fig 1 Simulation signal of impact fault

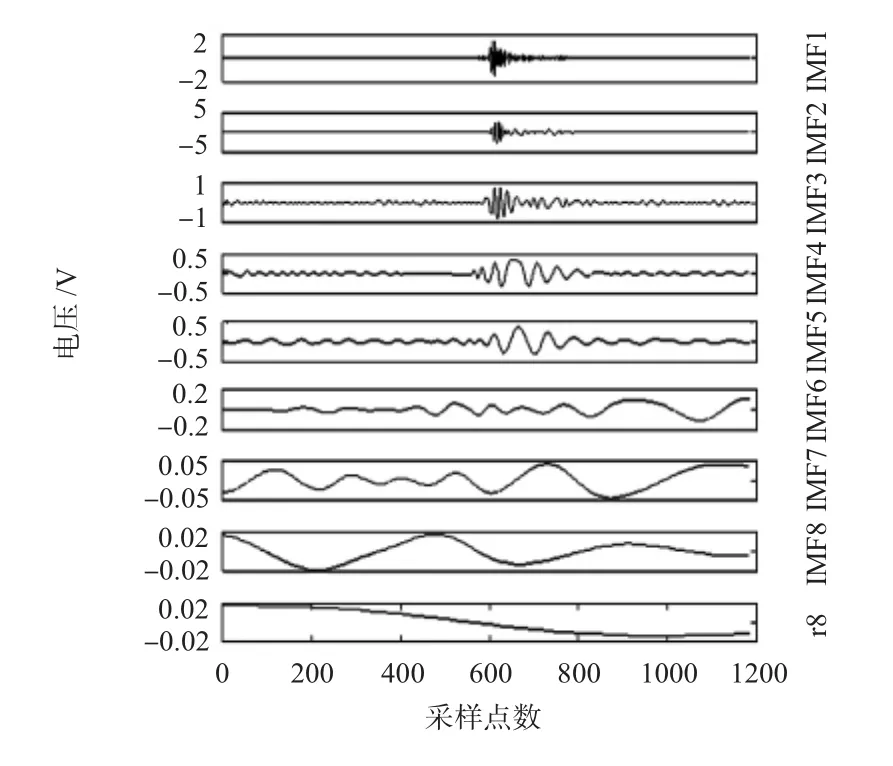
圖2 沖擊故障的EMD分解波形Fig 2 EMD decomposition waveform of impact fault

圖3是傳感器沖擊故障信號經EEMD的波形圖，沖擊故障輸出信號被分解為8個IMF分量和殘余項，每個IMF分量均清晰地表征了沖擊故障信號的詳細特征信息，沒有出現模態(tài)混疊現象。

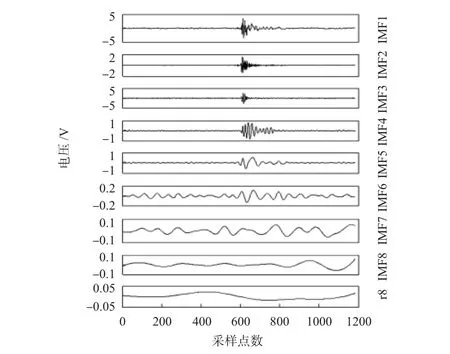
圖3 沖擊故障信號EEMD分解波形Fig 3 EEMD decomposition waveform of impact fault signal

根據EEMD能量熵分解步驟（1）～（5），分別對不同故障模式下的傳感器故障信號按照式（1）～（4）進行EEMD，并提取前8個IMF分量的能量熵，經過歸一化處理后形成傳感器故障特征向量，部分傳感器故障特征向量數據樣本如表1所示。

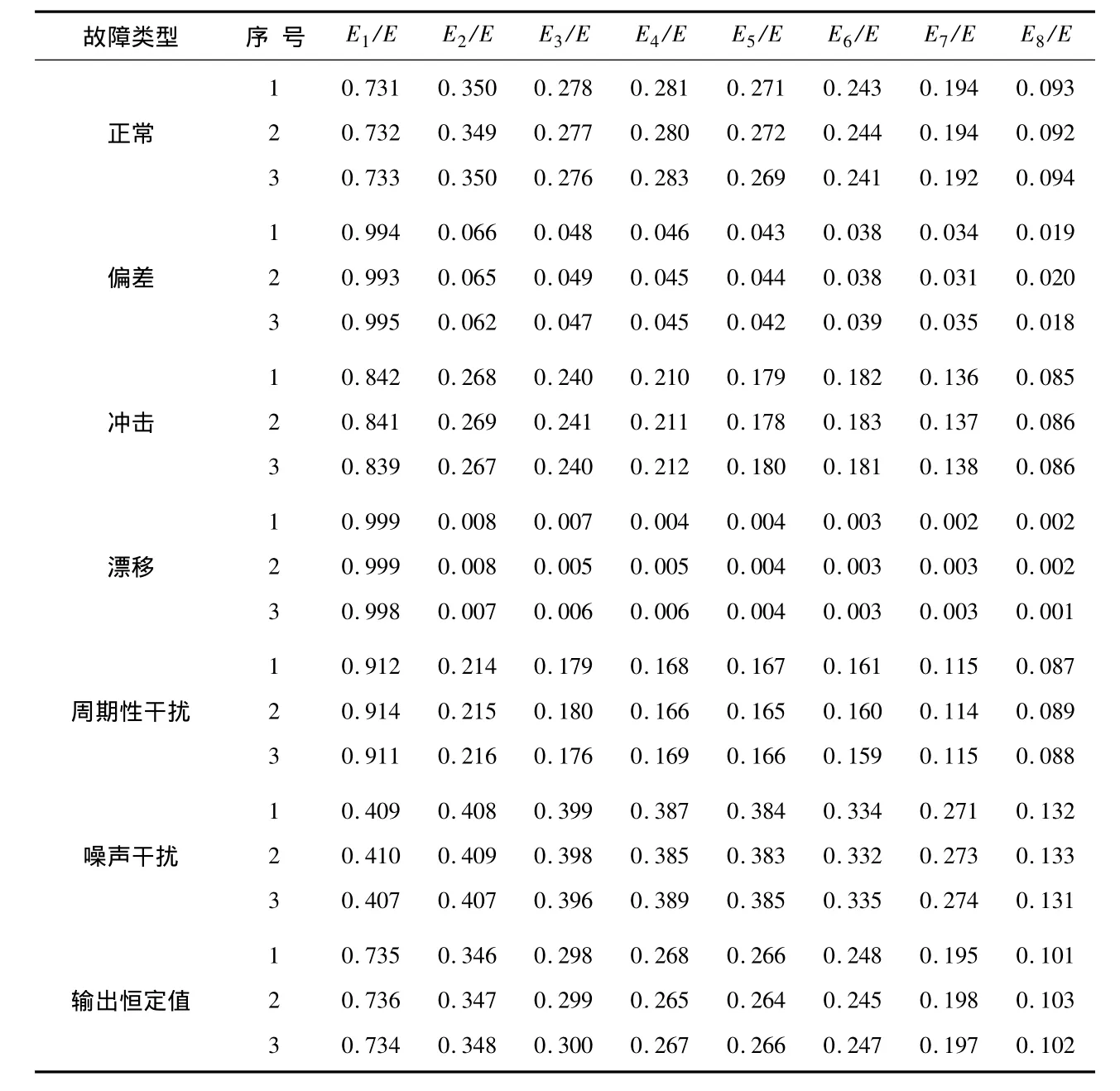
表1 基于EEMD能量熵故障特征提取方法的部分傳感器故障樣本Tab 1 Part of sensor fault sample based on EEMD energy entropy fault feature extraction method

3 LSSVM結構參數優(yōu)化

LSSVM的正規(guī)化參數γ和核函數參數σ2的選取直接影響到LSSVM的分類和泛化能力。常見的參數優(yōu)化算法有:試湊法、網格搜索法和三步搜索法等，前2種算法運算復雜用時長，未必能找到全局最優(yōu)解;三步搜索法雖然運算時間短，但是主要依靠人工經驗，不一定能尋找到最優(yōu)參數。

粒子群優(yōu)化（PSO）算法是一種基于迭代的啟發(fā)式并行搜索進化算法，是由美國學者Kennedy J和Eberhart R C［10］受鳥群覓食行為的啟發(fā)而提出的群智能優(yōu)化算法。

PSO算法是一種基于迭代的啟發(fā)式并行搜索進化算法，其速度和位置更新的方程如式（11）和式（12）所示

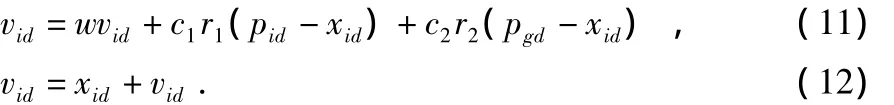
其中，vid和xid分別為粒子i在d維中的速度和位置;pid為粒子i在d維中的最優(yōu)值;pgd為所有粒子在d維中的最優(yōu)值;w為慣性權重;c1和c2為學習因子;r1和r2為 之間的隨機數。

4 實際測試分析

為了比較不同故障特征提取方法的分類性能，選取動車組制動系統(tǒng)的AS壓力傳感器作為研究對象，對7種傳感器狀態(tài)下各100組數據，然后隨機選取50組樣本進行訓練，利用余下的各50組進行測試。BP神經網絡采用8—16—7結構，小波包采用三層小波包分解，并提取小波包能量熵［2］。LSSVM采用“1—V—1”多類分類器，共設計21個兩類分類器。運用PSO算法對LSSVM模型的正規(guī)化參數和核函數參數進行優(yōu)化，得到最佳的正規(guī)化參數γ=115．26，核函數參數σ=0．54。根據不同的故障特征提取方法和故障診斷方法得到的診斷結果如表2所示。

表2 故障診斷結果Tab 2 Results of fault diagnosis

從傳感器故障分類識別結果可以看出:提出的基于EEMD能量熵的故障特征提取方法的故障分類結果正確率最高，對傳感器的沖擊故障、周期干擾故障和噪聲干擾故障的正確分類率達到100%，遠高于基于小波包故障特征提取方法和BP神經網絡分類方法的故障正確分類率，驗證了提出的故障特征方法和故障診斷方法的有效性。

5 結論

針對動車組制動系統(tǒng)的傳感器故障，提出了基于EEMD能量熵和改進LSSVM的故障診斷新方法。基于EEMD能量熵的故障特征提取方法可準確可靠地提取傳感器的故障特征信息，采用PSO算法優(yōu)化LSSVM的結構參數可以獲得更優(yōu)的結構參數組合，能夠顯著提高LSSVM的分類能力和泛化能力。實驗結果表明:提出的診斷模型既有較高的故障正確分類率，也有良好的泛化能力。

［1］ 馮志剛，王 祁，信太克規(guī)．基于EMD和SVM的傳感器故障診斷方法［J］．哈爾濱工業(yè)大學報，2009，41（5）:59 －63．

［2］ 馮志剛，王 祁，徐 濤，等．基于小波包和支持向量機的傳感器故障診斷方法［J］．南京理工大學學報:自然科學版，2008，32（5）:609－615．

［3］ 李歡歡，司風琪，徐治皋．一種基于魯棒自聯想神經網絡的傳感器故障診斷方法［J］．中國電機工程學報，2012，32（14）:116－121．

［4］ 陳楚瑤，朱大奇．神經網絡主元分析的傳感器故障診斷方法［J］．系統(tǒng)工程與電子技術，2010，32（7）:1549 －1553．

［5］ Lei Yaguo，Lin Jing，He Zhengjia，et al．A review on ensemble empirical mode decomposition in fault diagnosis of rotating machinery［J］．Mechanical Systems and Signal Processing，2013，35（1－2）:108－126．

［6］ Wu Zhaohua，Huang Norden E．Ensemble empirical mode decomposition:A noise-assisted data analysis method［J］．Advances in Adaptive Data Analysis，2009，1（1）:1 －41．

［7］ 蔣少華，桂衛(wèi)華，楊春華，等．基于RS與LSSVM多分類法的故障診斷方法及其應用［J］．中南大學學報:自然科學版，2009，40（2）:447－451．

［8］ Suykens J A K，Vandewalle J．Least squares support vector machine classifiers［J］．Neural Processing Letters，1999，9（3）:293－300．

［9］ 張 超，陳建軍，郭 迅．基于EEMD能量熵和支持向量機的齒輪故障診斷方法［J］．中南大學學報:自然科學版，2012，43（3）:932－939．

［10］ Kennedy J，Eberhart R C．Particle swarm optimization［C］∥Proceedings of IEEE International Conference on Neural Networks，NJ，1995:1942 －1948．