臨近空間目標運動建模與跟蹤方法研究

張 遠 吳 昊

(中國電子科技集團公司第38 研究所 合肥 230088)

0 引言

臨近空間高超聲速目標能夠在稀薄大氣層做持續的高超聲速運動，具有飛行速度快、機動能力強、投送能力遠、突防能力強的特點，將成為未來重點發展的武器裝備。目前由于探測手段和實際數據的缺乏，高超聲速目標是跟蹤領域新興的一類目標，沒有經過應用證明的實用跟蹤方法，對于它的研究還處于不成熟階段［1，3］。臨近空間目標探測雷達是我國下一步重點發展的探測裝備，因此研究高效的臨近空間目標跟蹤方法，提高該類目標的跟蹤性能，是雷達目標跟蹤領域的迫切需求。本文對臨近空間高超聲速飛行器的飛行特性進行分析，根據其動力學模型，建立臨近空間高超聲速飛行器的運動模型，采用交互多模型濾波(IMM)方法進行跟蹤。采用Monte-Carlo 仿真實驗，本文提出的目標運動模型和跟蹤算法對臨近空間高超聲速目標的跟蹤性能有明顯改善。

1 臨近空間目標的飛行特性

本文研究的高超聲速飛行器在30 km～60 km的臨近空間進行跳躍飛行，其飛行軌道如圖1 所示。

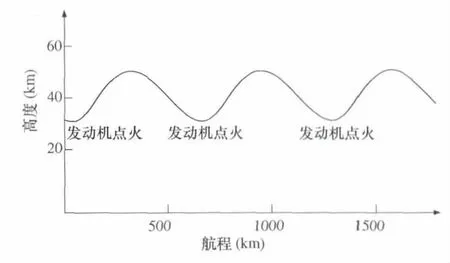
圖1 跳躍飛行軌跡

高超聲速飛行器在進入臨近空間后，一般采用跳躍飛行軌道，運動軌道簡化為3 個階段:助推段、巡航段和攻擊段。由于臨近空間高超聲速飛行器所特有的這種飛行特性，它能夠在很短的時間內完成加速，往往在巡航段開始幾百秒的時間內速度就可達到6～7 Ma。以X-51 為例，它由一架轟炸機攜帶飛至15.24 km 的高空后釋放，助推級點火工作約30 s，將飛行器推至18.29 km 的高空并達4.5 Ma;在助推級燃料燃盡后，助推級與中間級和巡航級分離，中間級分離后，巡航級在無動力狀態下滑翔數秒后，超然沖壓發動機開始進入高超聲速試驗階段，巡航級的發動機點火后工作300 s，使飛行器爬升到大約24 km 的高度，且速度達到7 Ma;發動機熄火后，飛行器在500 s 的下降階段內進行機動飛行［3］，并按此規律循環運動。

2 臨近空間目標運動模型

臨近空間高超聲速飛行器航程遠，建模時不能按飛機建模一樣把地面視為平面，但地球自轉等因素對運動過程的影響較小，一般可作如下假設:

a.地球是一個均勻球體，不考慮地球扁率，地球公轉及地球自轉;

b.大氣相對地球是靜止的且同一高度上均勻，忽略大氣參數的攝動;

c.飛行器為無動力返回的質點;

d.再入飛行器的側滑角為零。

基于以上考慮，在地心慣性坐標系中，臨近空間目標飛行器的動力學方程如下［1-2］:

其中:h 為高度;M 為馬赫數;γ 為航跡傾角;χ 為航跡方位角;λ 為經度;φc為緯度;c 為聲速;φv為速度滾轉角;R 為地球半徑;P 為推力;α 為迎角;D 為阻力;L 為升力;m 為飛行器質量;g 為重力加速度;Isp為比沖。

阻力D 與阻力系數CD，機翼面積S，大氣密度ρ和飛行器速度v(即Mc)有關，具體表達式為:

升力L 與升力系數CL，機翼面積S，大氣密度ρ和飛行器速度v 有關，具體表達式為:

重力加速度g 表示為:

其中地球引力常數μ=3.986004418 ×1014。大氣密度的標準分布取為指數規律

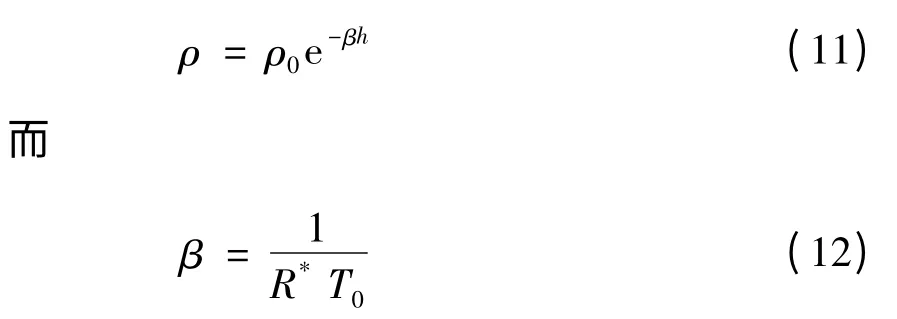
其中R*為以重力工程制單位表示的海平面干燥空氣之氣體常數，其值為R*=29.27kg·m/kg·℃，T0為海平面的絕對溫度，取為T0=288.15K，ρ0為海平面大氣密度，取為ρ0=1.2250kg/m3。

3 臨近空間目標跟蹤算法

從式(1)～(12)可以看出，臨近空間目標的運動模型復雜，機動性強，常規的目標跟蹤方法對該類目標的跟蹤性能差，甚至無法跟蹤。目前普遍認為最好的高速高機動目標跟蹤算法是交互多模型濾波方法，該濾波方法不需要建立準確的目標運動模型，而是采用多個模型的組合來逼近目標的真實運動狀態，模型之間的轉移概率通過計算濾波殘差進行調整。與單模型自適應算法相比，交互多模型算法具有以下顯著的優點:

a.由于對參數空間采用的多模型描述，可以通過適當的擴充模型來達到對建模的細化，通過實時的增減和變更模型，可增強變結構的自適應能力;

b.算法的計算量與選用的模型數幾乎是線性關系，而其性能與二階廣義偽貝葉斯算法相當;

c.在濾波過程中，通過模型概率的變動實現自適應的變結構;

d.算法具有明顯的并行結構，便于并行運算實現。

IMM 濾波中，運動模型的選擇直接關系到目標跟蹤性能，根據臨近空間目標的高速高機動的運動特性和目標模型的特點，本文采用CV 模型、CA 模型和Singer 模型的三模型交互濾波器。

CV 模型將目標的運動先驗地定義為勻速，機動被看作是一種隨機的輸入，其大小體現在過程噪聲的協方差矩陣中。

CA 模型是假設加速度的一階導數是白噪聲的過程。

Singer 模型用目標機動幅度和目標機動的持續時間描述一維機動，運動目標的加速度模型不是通常假定的白噪聲模型，而是相關噪聲模型。

基于CV+CA+Singer 模型的IMM 濾波算法結構［4-5］如圖2 所示。

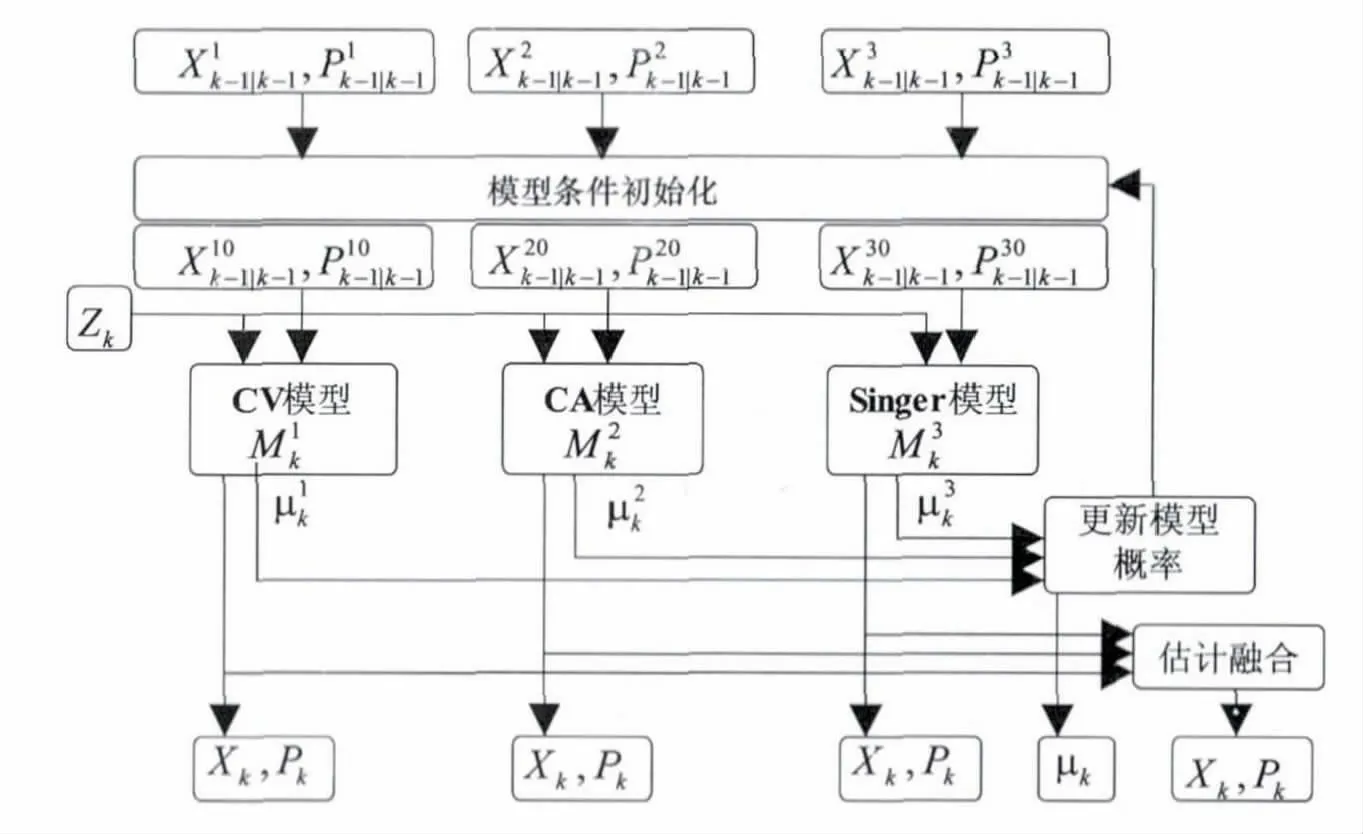
圖2 IMM 算法結構圖

IMM 算法的遞推處理過程如下:

a.狀態估計的交互

假設從模型i 轉移到模型j 的轉移概率為ptij

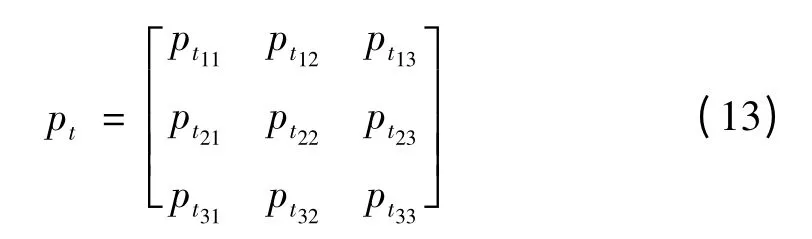
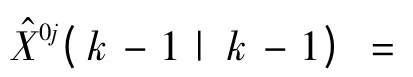
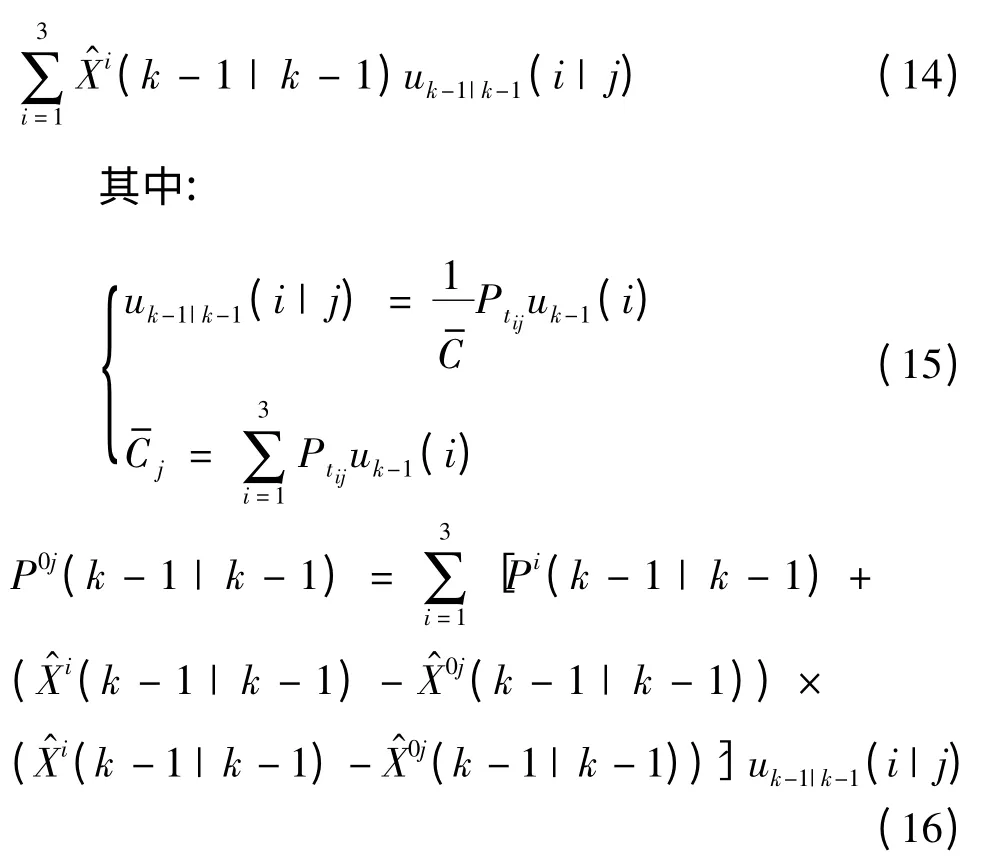
b.模型修正

c.模型可能性計算

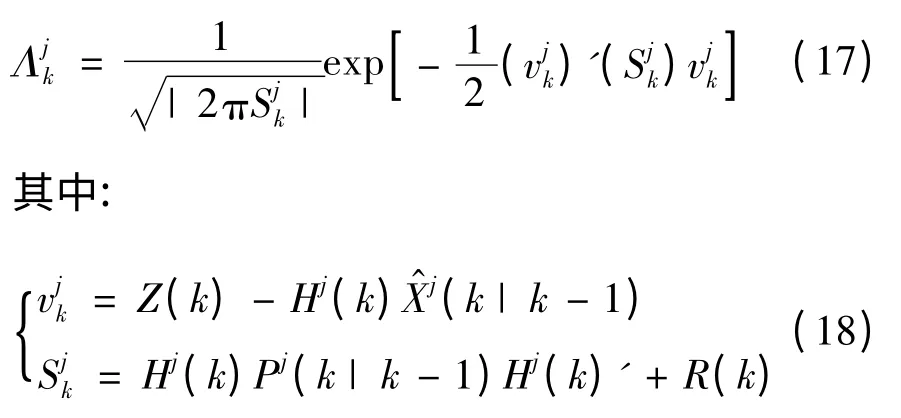
d.模型概率更新

模型j 的概率更新如下:

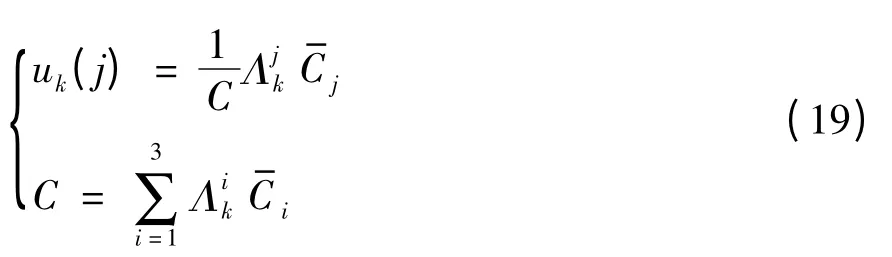
e.輸出交互

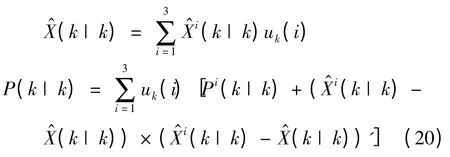
4 仿真分析

4.1 仿真場景

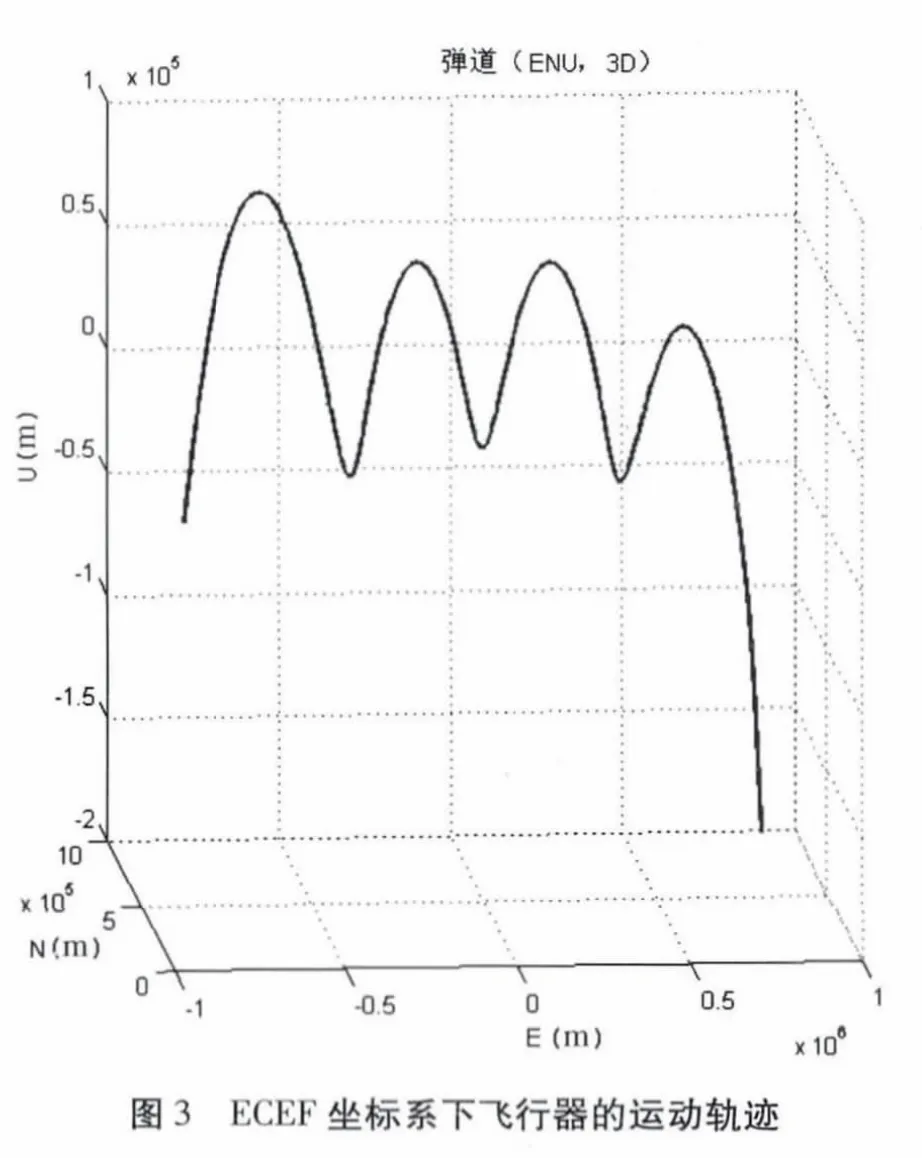
按(1)～(12)的動力學模型，得到臨近空間目標在地心固定坐標系中的軌跡如圖3 所示。從圖中可以看出目標的運動軌跡與實際飛行的軌跡曲線相似，說明本文的建模方法正確。

設定雷達位置，將地心固定坐標系中的軌跡轉換為雷達測量的距離、方位、仰角坐標如圖4～圖6。目標的速度變化曲線如圖7。

4.2 仿真結果分析

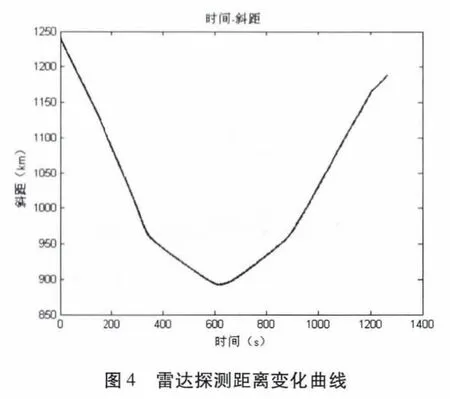
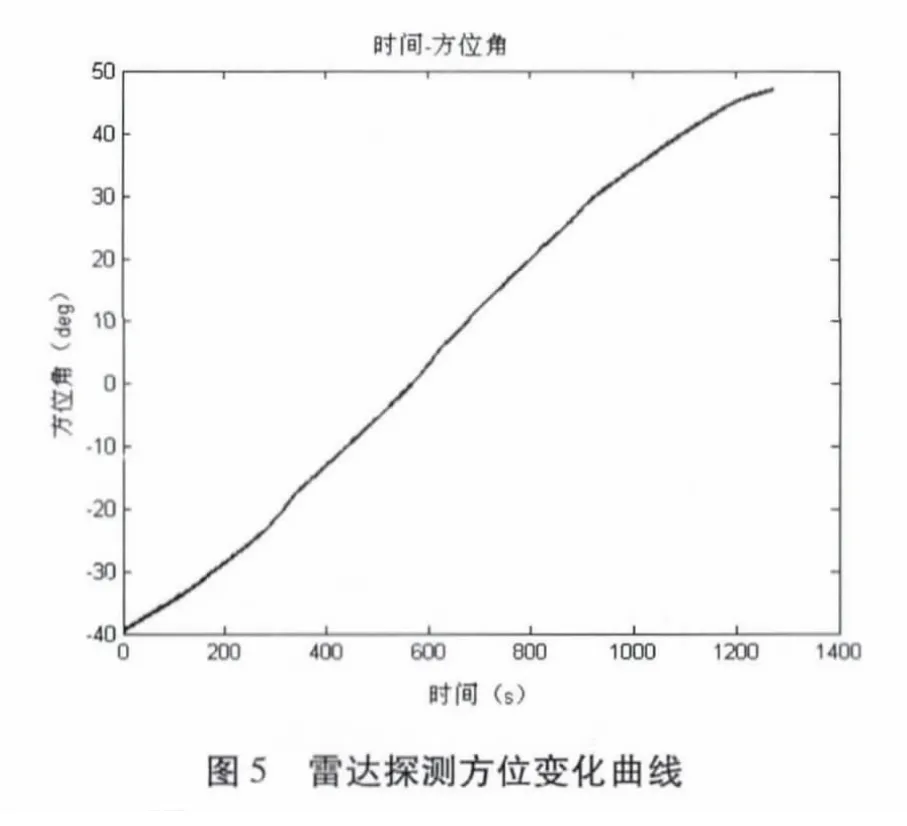
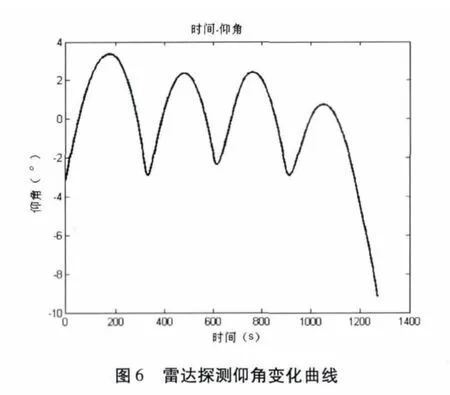
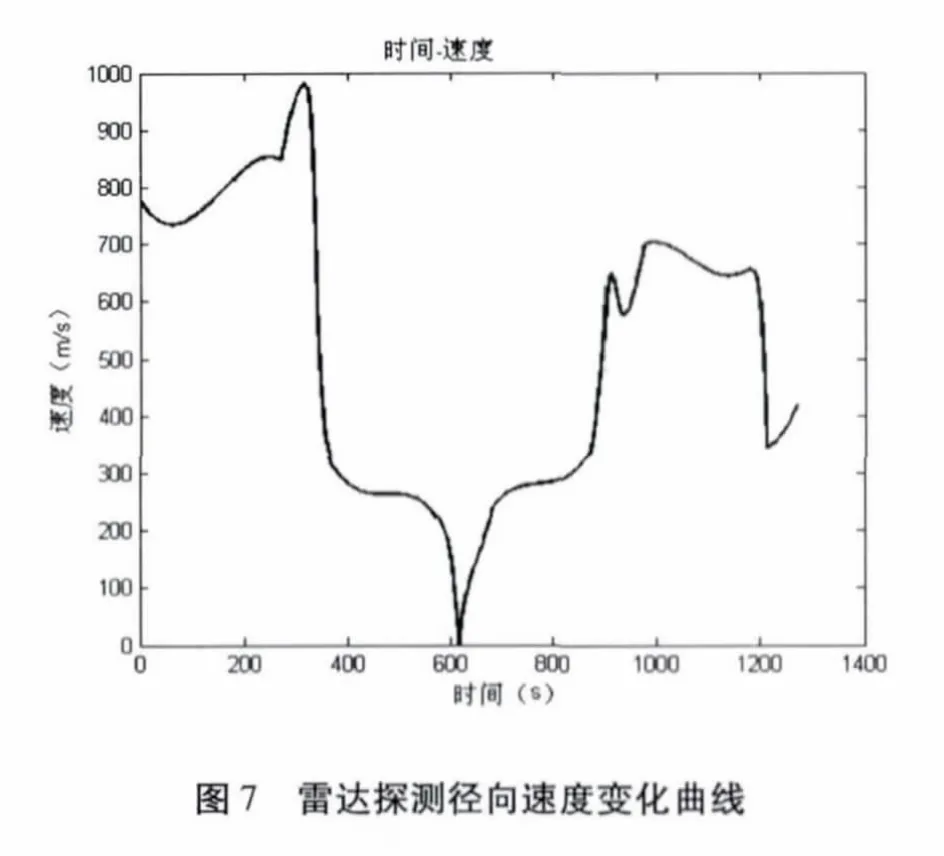
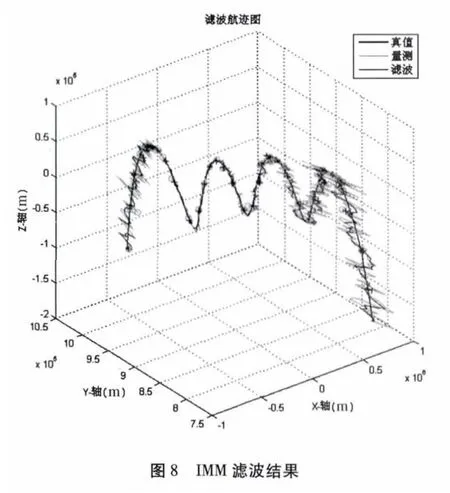
假設雷達采樣數據率為1Hz，距離精度為150m，方位精度為1°，仰角精度為1°，在圖4～圖6 的理想數據中增加雷達探測誤差，產生雷達探測的點跡數據。對此數據應用式(13)～(20)的IMM 濾波算法進行濾波。雷達點跡與濾波后的航跡如圖8 所示，濾波后的方位一次差如圖9，距離一次差如圖10 所示，仰角一次差如圖11 所示，經統計計算，濾波后航跡的距離精度為93.8464m，方位精度為0.6571°，仰角精度為0.7205°，明顯優于雷達量測點跡。

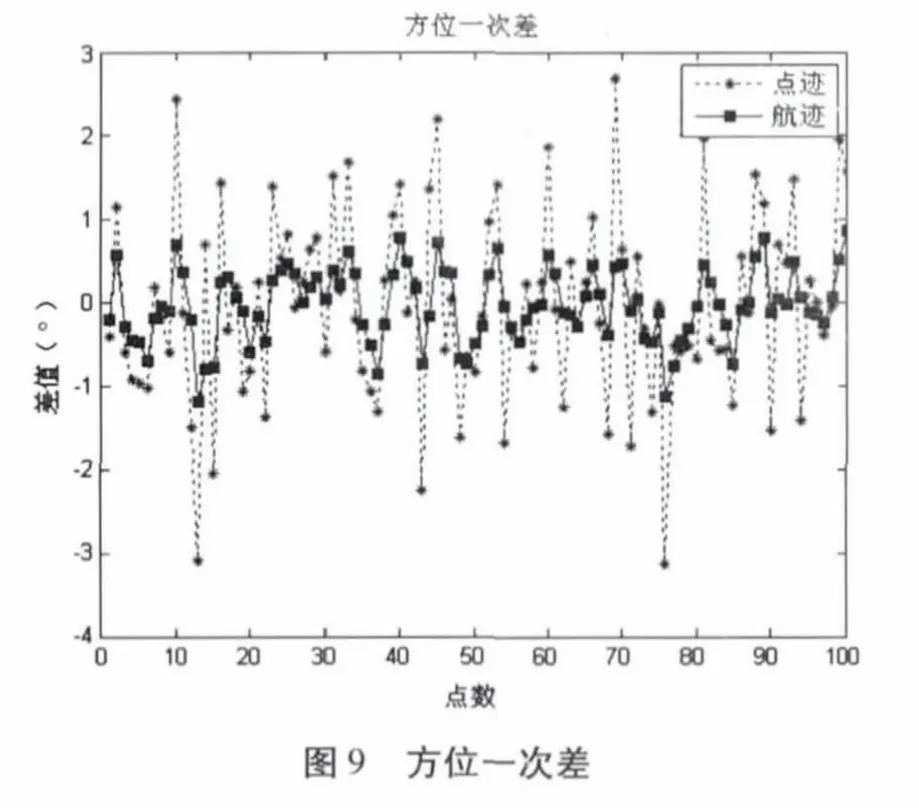
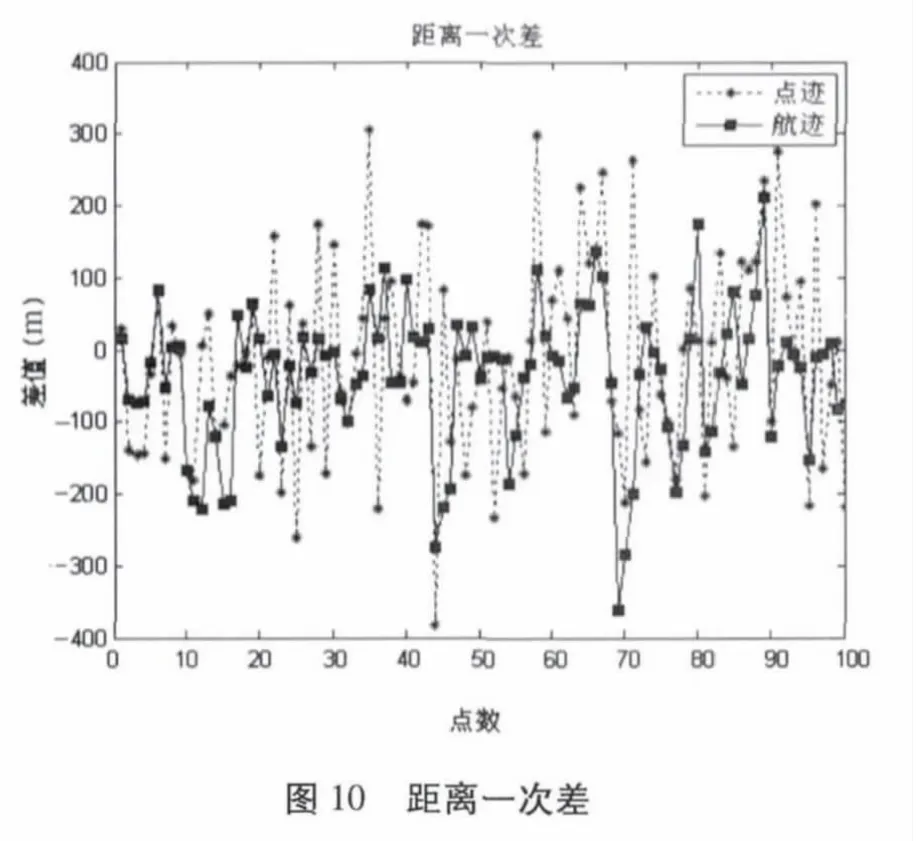
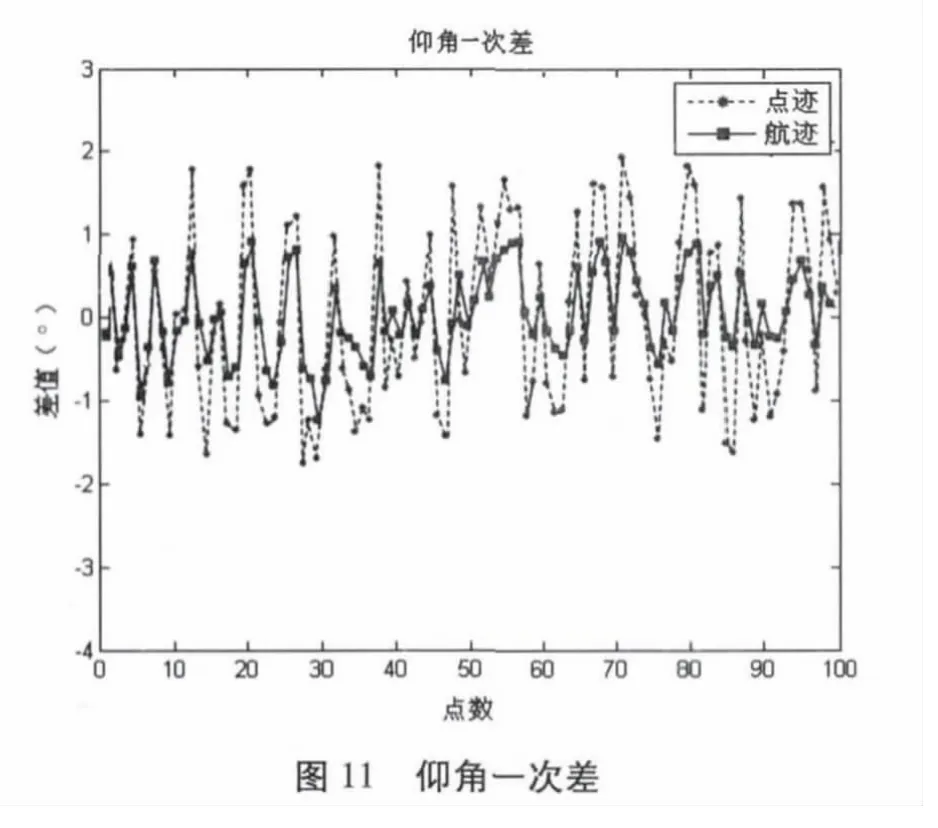
圖8～圖11 表明:

a.IMM 算法能夠對臨近空間目標進行跟蹤，驗證了該方法在臨近空間目標跟蹤應用上的可能性;

b.利用IMM 算法進行濾波后所得到的目標航跡精度明顯優于通過點跡精度，驗證了該方法在臨近空間目標跟蹤應用上的有效性;

c.本文建立的臨近空間高速目標模型軌跡與實際目標飛行軌跡逼近程度較高，能作為雷達算法仿真的輸入。

5 結束語

本文對臨近空間飛行器進行特性分析和建模，采用IMM 算法對其進行跟蹤，仿真結果表明，IMM算法具有較好的臨近空間飛行器跟蹤性能，跟蹤精度提高明顯，為雷達進行臨近空間目標跟蹤提供了一種方法。但本文提供模型未經實際數據比較，模型的準確性還需進一步驗證。

［1］肖業倫.航空航天器運動的建模-飛行動力學的理論基礎［M］.北京：北京航空航天大學出版社，2003.

［2］孫勇.高超聲速飛行器再入過程改進氣動參數模型［J］.系統工程與電子技術，2011，33(1) .

［3］關欣，趙靜.一種可行的高超聲速飛行器跟蹤算法［J］.電訊技術，2011，51(8) ：81～83.

［4］Mazor E，Aveebuch A，Bar-Shalom Y，et al.Interacting multiple model methods in target tracking：a survey［J］.IEEE Transactions on Aerospace and Electronic Systems，1998，34(1) ：103-122.

［5］何友，修建娟，張晶煒等.雷達數據處理及應用［M］.北京：電子工業出版社，2009.