基于線性調頻擴頻定位的動態誤差修正算法

席通專，丁希侖

（北京航空航天大學機械工程及自動化學院，北京 100191）

0 引言

隨著無線傳感器網絡技術的發展，其低成本、低能量消耗、多功能［1］等特點吸引了大量研究，已經被廣泛應用于物聯網、人員定位、機器人定位等眾多領域。定位功能是無線傳感器網絡的一大特點，與傳統定位技術相比有組網靈活、成本低等特點。本文所采用的線性調頻擴頻技術（chirp spread spectrum，CSS）是基于IEEE802.15.4a的物理層標準的無線傳感器技術，在中短距離內具有良好的定位精度和穩定性。

CSS技術是基于信號傳播時間（TOA）的測距，獲得節點之間的距離值后，可以采用無線傳感器網絡中常用的基于距離的定位算法進行定位。目前CSS定位的誤差修正主要研究CSS傳感器本身結構特點和底層協議來提高測距精度，結合多個測距信息來反饋修正誤差的研究不多，這樣可以使測量距離得到相互修正。近年來，Ming Cao等人在文獻［2，3］中把Cayley-Menger行列式［4］引入定位中，推導出了平面定位誤差滿足的二次約束方程，這對定位誤差修正研究意義重大。利用誤差的距離幾何約束方程來對誤差進行最優估計的研究進展卻不多。Ming Cao提出了一種基于距離幾何約束方程轉化為求誤差平方和的最值問題來估計測量誤差。文獻［5，6］中，在不同定位系統中應用Ming Cao提出的方法來進行測距誤差修正，再結合定位算法來提高定位精度，并進行了仿真分析驗證。他們的研究僅采用仿真方法對算法進行驗證，沒有進行定位實驗評估算法效果，本文通過分析Ming Cao的基于距離幾何約束的誤差平方和最小值來估計誤差的方法后，發現該方法對定位精度的改善并不明顯，本文實驗也證明了這點。

根據上述分析，本文提出了一種結合測距誤差模型與距離幾何約束方程來對視距環境下0定位進行距離修正，給出實際定位中每個位置點的最優測距誤差模型，再用這個系數在一定范圍內變化的線性方程對測量值進行動態修正。文章第1節分析了視距環境下CSS測距誤差模型特性，第2節介紹了距離幾何約束方程，分析Ming Cao的誤差平方和最優解問題來修正誤差算法，然后提出了結合測距誤差模型和距離幾何約束的動態修正算法，文章最后部分通過室內CSS定位實驗比較了動態修正算法、Ming Cao的距離幾何約束算法及普通靜態修正算法的效果。

1 CSS測距誤差模型分析

線性調頻擴頻技術以前主要用于脈沖壓縮雷達，能夠很好地解決沖擊雷達系統測距長度和測距精度不能同時優化的矛盾。IEEE將CSS技術列為802.15.4a技術標準的底層實現方式之一之后，CSS技術被越來越多被用于無線定位。CSS系統通過測量信號傳播的時間來計算距離，采用一種對稱雙向兩次測量法（SDS-TWR）［7］。該方法不需要節點之間時鐘同步即可完成測量，減少時鐘漂移帶來的誤差。CSS定位系統測距精度雖然比其他的無線傳感器網絡高，但測量距離也包含了噪聲和誤差。誤差主要來源于兩部分，定位系統自身所引起的誤差和外部環境引起的誤差。CSS自身所引起的誤差為系統性誤差，主要是由傳感器的自身所有的參數如時鐘精確性、天線性能等導致的偏移距離。同時系統還存在由于非視距、多經效應和具體環境特點帶來的誤差，非視距環境會導致CSS系統出現比較大的誤差。由于本定位系統所應用的環境特點，研究視距范圍內的誤差修正，本文所提出的方法在非視距環境下并不能保證良好性能。

在視距環境下，CSS系統測距模型大致滿足線性關系，模型的系數與測距傳感器本身參數和環境有關，先通過測距測試研究CSS系統在視距環境的測距模型。測試分為兩組，一組研究同一對測距模塊在不同環境下的測距誤差模型，一組研究兩對不同測距模塊在相同環境的測距誤差模型。

測試1:選擇一對測距模塊，固定其中一模塊，另一個模塊依次放置在設定距離點測量;在室內不同位置環境重復上述測試。

測試2:選擇兩對測距模塊，每一對測距模塊在同一位置環境按照實驗1測距方法進行測量。

得到測試結果后，通過最小二乘擬合得到相應的測距誤差模型，數據點及擬和曲線如圖1所示，（a）、（b）為測試1結果，（c）、（d）為測試2研究結果，擬合方程如下:

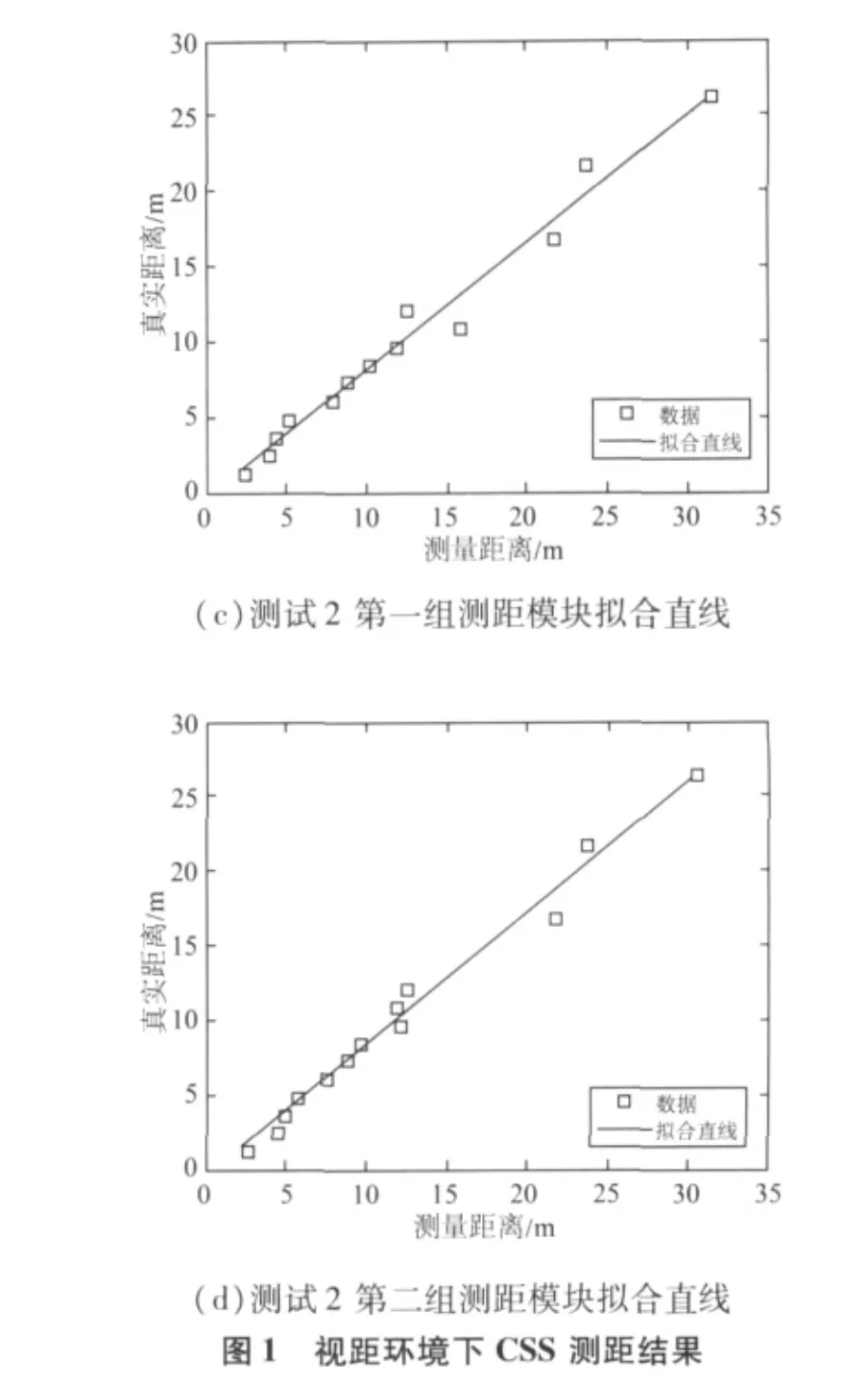
上面的測試結果驗證了存在誤差和其他干擾的CSS測距模型線性關系的系數并不是固定的，環境的變化、節點的不同，甚至測距模塊的姿態變化，都會引起測距模型系數的變化。如果有非視距或其他多徑效應存在，測量距離與真實距離可能不滿足線性關系，或者擬合直線的系數會變動很大，此時擬合方程式沒有意義。因此，視距環境下的CSS定位中有以下測距誤差模型為:

其中:d是真實距離;d是測量距離;a，b為線性方程系數。其中a1，a2，b1，b2可以根據定位前對定位模塊進行測距測試擬合所得系數平均值附近的一個較小區間。如果擬合系數超過所取范圍，則認為有較大噪聲干擾，仍然認為測距誤差模型在式（5）的范圍內。

目前視距范圍內減少誤差的方法一般是取測距測試所擬合的測距誤差模型方程作為修正方程對測量結果進行修正，即在整個定位中不考慮節點之間的差異、環境特點等導致測距誤差模型方程的差異，而采用同一方程對結果進行修正，本文中把這種方法叫做靜態誤差修正算法，研究根據每個定位最小單位（三個錨節點，一個待測節點，如圖2所示）內利用三個測量距離，然后通過距離幾何約束尋找最優的測距模型方程d=a*d+b*，最大限度地動態修正誤差，第2節詳細介紹了誤差修正過程。

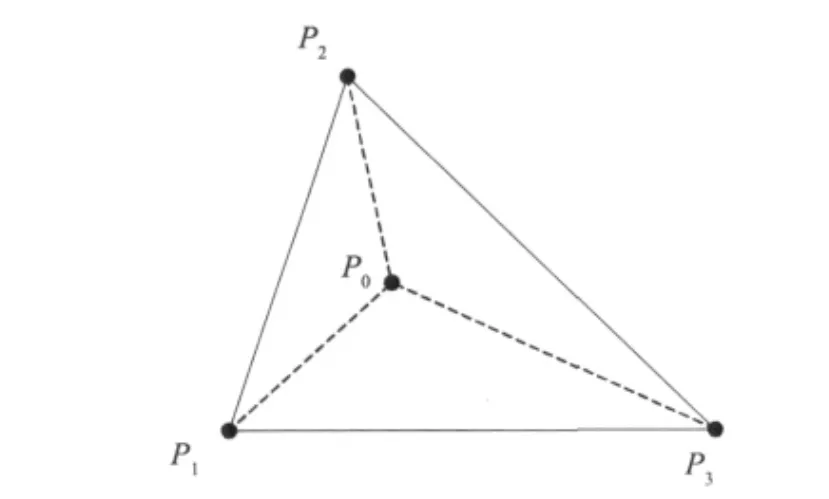
圖2 三個錨節點定位示意圖

2 距離幾何約束及動態誤差修正算法

2.1 Cayley-Menger行列式及距離幾何約束修正誤差法分析

式中d（pi，qj）表示點pi和qj之間的歐幾里得距離。兩個點序列的Cayley-Menger雙聯行列式［4］定義為:

當兩個點序列是同一序列時，用D（p1，…，pn）表示D（p1，…，pn;q1，…，qn）用 M（p1，…pn）表示 M（p1，…，pn;q1，…，qn）并把 D（p1，…，pn）叫做 Cayley-Menger行列式。

Cayley-Menger行列式有下面比較經典的結論:

定理1.（距離幾何基本定理）考慮m維空間由點p1，…，pn組成的n元組。如果n≥m+2，則Cayley-Menger矩陣M（p1，…，pn）是奇異的，即:

圖2為基于距離定位的一個常用最小定位單位，其中已知三個錨節點1，2，3的位置坐標，由無線傳感器可以測得待測節點0到錨節點1，2，3的之間距離。待測節點0到錨節點1，2，3，4的測量距離記為，i=1，2，3;4個節點之間的實際歐式距離記為 dij=d（pi，pi），i，j=0，1，2，3＆i≠j。定義測量誤差 εi為:

則由定理1 知，D（p0，p1，p2，p3）=0，聯立D（p1，p2，p3）≠0，Ming Cao等人在文獻［2，3］中推出以下誤差關系式:

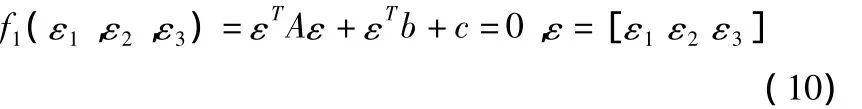
其中:A是3×3階矩陣，b是3×1階矩陣，c是一實數，且A，b，c是由dij表達的。可以看出式（10）是僅關于三個誤差值的一個約束方程。

在此基礎上，Ming Cao等提出了基于距離幾何約束方程的誤差估計方法。通過一個最小二乘法問題來求解最優值來估計誤差如式（11）所示，本文中把這種方法叫做距離幾何約束Ming Cao修正法。

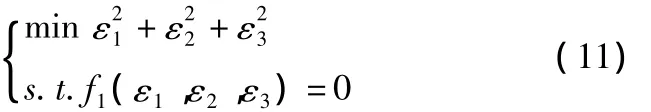
為了解決上述問題，下面部分根據CSS測距特點提出了誤差動態修正方法，充分利用了距離幾何約束方程把測量距離誤差建立聯系并達到相互修正的作用。

2.2 基于距離幾何約束方程的動態誤差修正算法

對于CSS定位系統來說，如第1節分析，視距環境下CSS測量距離非嚴格滿足線性關系，且線性方程的系數也隨著不同測距模塊、測距環境等在一個范圍內變化。實際定位中定位節點數量眾多，不可能提前測試好每對節點之間的測距誤差模型系數，即使能測也是沒有意義的，因為測量過程中測距模塊的位置、位姿、信道等變化都會引起系數變化。

目前針對上述問題的處理方法多采用如第1節所述靜態修正算法。但是這種修正方法有明顯不足，CSS測距系統是一種高精度的系統，在100 m范圍內測距誤差僅僅2～3 m，而測距誤差模型修正的距離是同一個數量級數據，采用不準確測距模型方程修正后誤差依然可能很大。因此采用更準確的測距誤差模型是很必要的，最好的解決方法是能估計出最小定位單位中待測節點與三個錨節點的三個測距誤差模型，但是由于約束方程數目不夠求解出每個模型系數。本算法則假設最小定位單位中三個測距誤差模型為同一模型，然后再根據距離幾何約束條件找出這一最佳估計。在本算法中，把使得距離約束方程f1（ε1，ε2，ε3）取得最接近0的系數作為一個最小定位單位的最佳測距誤差模型。滿足距離幾何約束為0的測距誤差模型可能有多個，但是根據第1節研究，視距環境下的測距誤差模型系數一般在一個范圍內，而把超出這個范圍系數的測距誤差模型認為是其他較大隨機誤差或非視距等引起的，或是數學方法求出的無效解。研究中只考慮在已知系數范圍內使距離約束方程左邊最接近0的一組系數解為最佳測距誤差模型的系數。

根據第一節的研究，根據定位實驗前測距實驗擬合測量模型方程，選取多個擬合測距誤差模型系數的平均值作為中位置，然后選擇中位置附近的一個區間 a∈［a1，a2］，b∈［b1，b2］作為求解最佳測距誤差模型系數區間。聯立

式（5）和式（9）得到以下方程組，

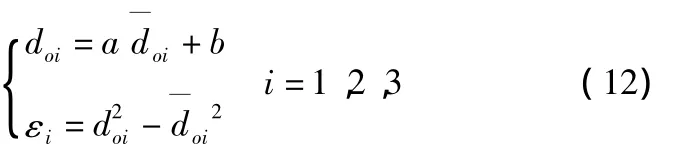
由式（12）可以推出:

把εi帶入距離幾何約束方程式（10），得到關于未知數a，b的函數，記為

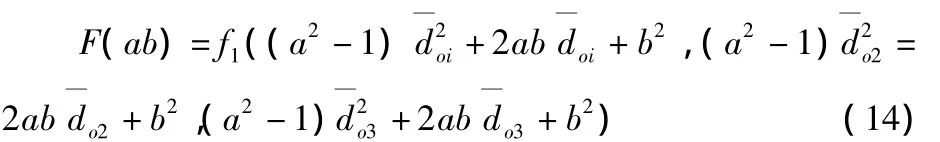
在 a∈［a1，a2］，b∈［b1，b2］內 F（ab）最接近 0 所對應的一組a*，b*就是測距誤差模型的最佳系數估計.因此求解最佳測距誤差模型方程的問題就轉化為如式（15）的一個最優值求解的問題，

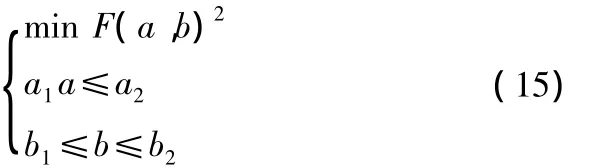
通過數值方法可以求解出系數的最優估計:a*，b*。求解出最佳測距誤差模型d=a*+b*后，利用這個模型對測量距離進行修正，修正后的距離采用平面定位方法如三邊法等即可求得待測節點位置坐標。動態誤差修正算法的意義在于能夠更準確的修正測量距離，修正后的距離再采用任何其他定位算法都提高定位精度，但是本算法相對于靜態修正算法增加了計算量。

3 實驗及結果分析

3.1 實驗設計

本定位實驗采取Nanotron公司開發的CSS測距模塊。實驗場地為室內15.2 m×15.2 m的空間，中間無障礙物，測距模塊安裝在1.5 m等高的支架上，三個錨節點位于P1（0.95，0.95），P2（14.25，14.25），P3（14.25，14.25），定位位置如圖3所示的25個點上，圖中每格距離為1.9 m。待定位節點依次放置在這25個位置上。

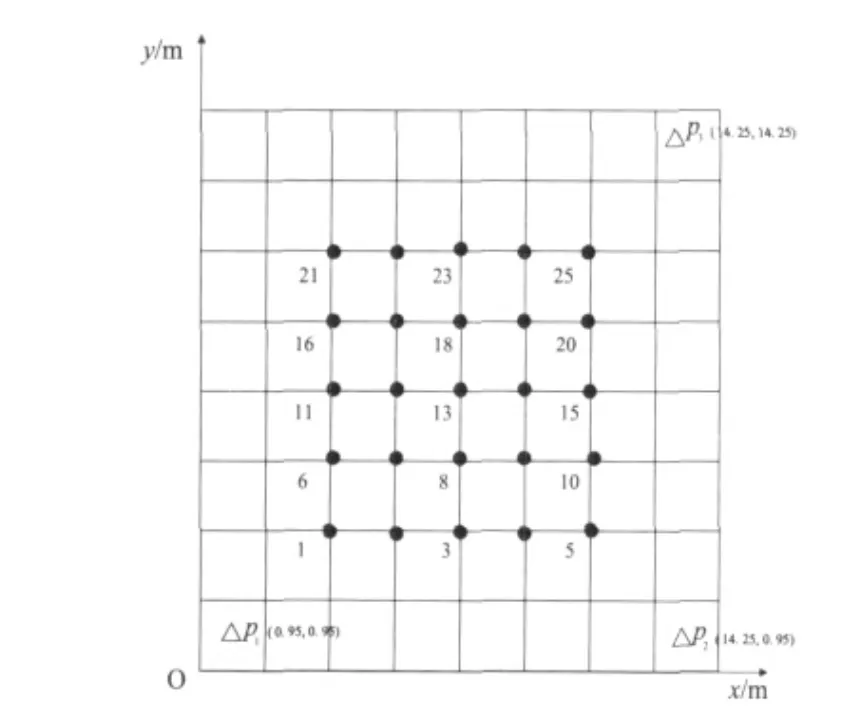
圖3 定位實驗布置圖

3.2 實驗結果分析

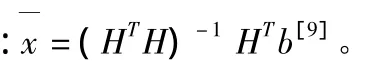
用式（16）作為定位誤差來評價三種定位算法效果:

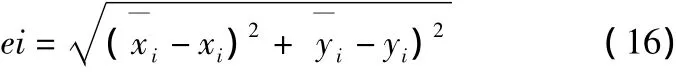
圖4 定位誤差對比圖

從圖4可以看出，本文所用方法在92% 的點比距離幾何約束Ming Cao法和靜態修正法有明顯精度改善，距離幾何約束Ming Cao修正法與靜態修正法效果近似。定位誤差去掉最大3個點和最小3個點計算出三種方法的誤差值的平均值。通過表1中可以看出動態修正法的三項誤差指標都遠遠優于距離幾何約束Ming Cao修正法和靜態修正法，動態修正的誤差是靜態修正法誤差的61%，距離幾何約束Ming Cao修正法的68% 。由此可得，本文所用誤差動態修正方法大幅提高了定位精度。同時，本文所用方法修正的測量距離可以與其他定位精度更高的基于距離的定位算法結合，將能進一步提高定位算法的精度。

表1 實驗指標對比

4 結論

CSS定位系統具有良好的視距環境下定位精度。距離幾何約束方程準確地描述了平面定位中誤差之間關系，能夠用于測量距離誤差修正。本文所提出的結合測距誤差模型與距離幾何約束方程的動態修正算法能有效地修正視距環境下CSS定位系統測量誤差提高定位精度，效果好于其他常用方法。

［1］G.Mao，B.Fidan，B.D.O.Anderson.Wireless Sensor Network Localization Techniques［J］.Computer Networks，2007，Volume 51，Issue 10，Pages2529-2553.

［2］M.Cao，B.Anderson，A.Morse.Localization with imprecise distance information in sensor networks［J］.44th IEEE Conference on Decision and Control，and the European Control Conference，2005，pp.2829-2834.

［3］M.Cao，B.Anderson，A.Morse.Sensor network localization with imprecise distances［J］.Systems ＆ Control Letters，2006，pp.887-893.

［4］G.M.Crippen，T.F.Havel，Distance Geometry and Molecular Conformation［M］.Wiley，New York，1988.

［5］J.Zheng，C.Wu，H，Chu.Localization algorithm based on RSSI and distance geometry constrain for wireless sensor network［J］.Electrical and Control Engineering（ICECE），2010 International Conference on，2010，2836-2839.

［6］朱建新，高蕾娜，張新訪.基于距離幾何約束的二次加權質心定位算法［J］.計算機應用，2009，29（2）.

［7］IEEE Standard，IEEE Std 802.15.4a，Aug.2007.

［8］Leonard M.Blumenthal.Theory and Application of Distance Geometry［M］.Oxford:Oxford University，1953.

［9］A.H.Sayed and N.R.Yousef，"Wireless location，"in Wiley Encyclopedia of Telecommunications， J. Proakis， Ed. New York:Wiley，2003.