新型三平動并聯機床的運動分析

李琳，李開明

（南京理工大學機械工程學院，江蘇南京 210094）

0 前言

并聯機床是在現代數控技術、機床技術和機器人技術基礎上發展出的一種高精度、高柔性的制造設備。同串聯機床相比，并聯機床具有獨特的優點，克服了串聯機床存在的缺點［1］。它將空間并聯機構的特點應用到機床中，綜合利用計算機軟件、電子控制等設備，取代部分機械傳動，能夠很方便地實現較復雜的空間運動。與傳統機床相比，并聯運動機床具有結構簡單、剛度高、動態性能好、反應速度快、可重構等優點［2］。由于并聯機床理論上所具有的一系列優點，近年來已成為一個十分熱門的研究方向。但是在實際應用中，還有許多技術問題尚待攻克。

并聯機構的復雜性首先表現為并聯多閉環機構內在的運動學的復雜性。奇異位形是機構的一個非常重要的運動學特性，機構的運動受力、控制等各方面的性能都與此有密切關系。在并聯機構的研究中，當并聯機構處于奇異位形時，其操作平臺具有多余自由度，此時機構就會失去控制。奇異性是并聯機器人機構學研究的重要內容，本文對并聯機床的奇異性和平穩性進行深入研究，為并聯機床結構確定關鍵技術參數提供依據。

1 運動學方程的建立

該并聯機床通過六條支鏈連接上下兩平臺，六根絲桿兩兩平行，即 A1B1//A2B2，A3B3//A4B4，A5B5//A6B6。下平臺固定，上平臺可進行平動，六根結構、長度相同可以分別調節的支撐桿用球面副連接上下兩平臺，其中有兩組桿與上平臺鉸接時采用了復合鉸鏈設計，通過特定的鉸鏈布置和支鏈伸縮桿同步驅動限制了末端執行器的三個轉動自由度，實現機構三維移動。

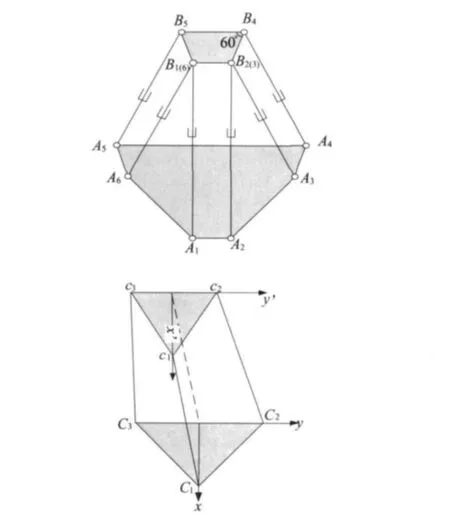
圖1 機構簡圖

首先建立坐標系［圖1（b）］。固定坐標系O－xyz固聯于下平臺，坐標中心O與下平臺幾何中心重合，Ox軸與OB1重合，Oy按右手定則確定，Oz軸垂直于固定平臺向上。動坐標系 P － x＇y＇z＇與上平臺固聯，中心 P 與上平臺幾何中心重合，x＇軸與Pc1重合，y＇按右手定則確定。

下平臺各鉸鏈中心點Ai及組桿鉸鏈點Ci（圖2）在固定坐標系中的坐標為:

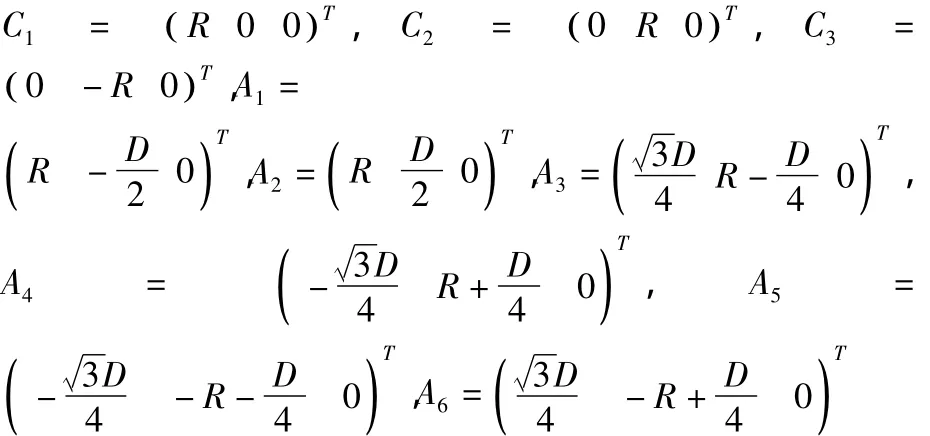
圖2 下平臺

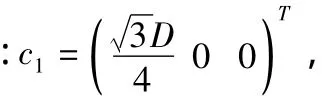
其中 B5B6=B3B4=B1B2=D=r。

設上平臺坐標系P－x＇y＇z＇原點 P 在定坐標中坐標為（xp，yp，zp），則齊次變換為:

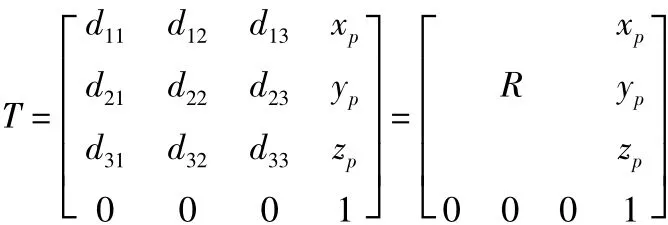
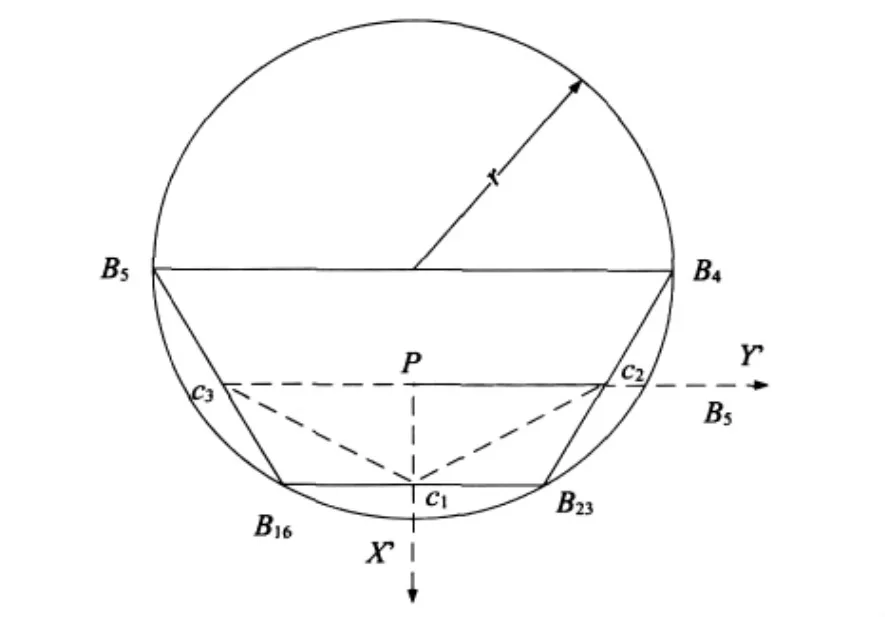
圖3 上平臺

其中R表示動坐標系對定坐標系的方向余弦。則動平臺上的鉸鏈點ci在固定坐標系中的位矢可表示為:

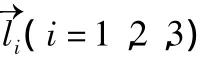
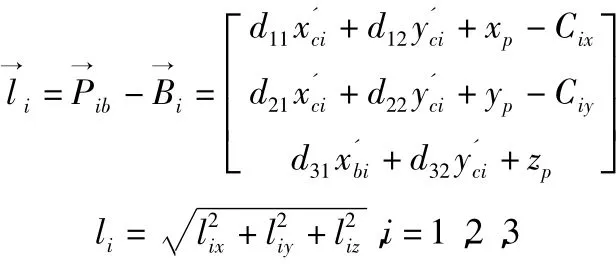
由于本文的研究對象為三自由度平動機構，

并聯機構的復雜性導致機構的位置正解難度較大，但本機構由于具有特殊性，具有唯一解析正解。其解如下:

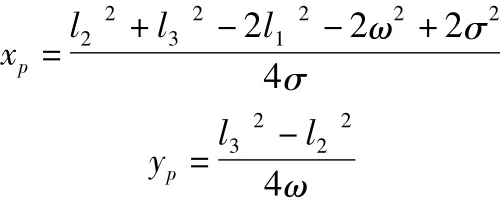
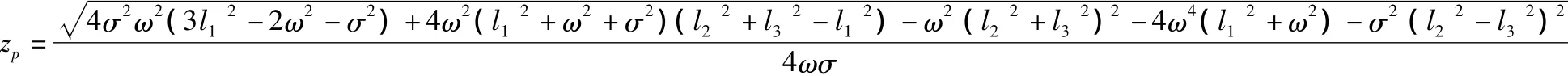
2 奇異性

當機構處于某些特殊位置時，其雅克比矩陣將成為奇異陣，其行列式的值為零，機構的速度正反解不存在。把并聯機構的這些特殊位置稱為奇異位形或特殊位形。奇異性是并聯機床結構參數設計所需考慮的重要因素。當并聯機床處于奇異形位時，機構將獲得多余不可控的自由度或者變得剛化而失去部分自由度。機構自由度的喪失意味著機構某種功能的喪失，而機構獲得額外的自由度則會導致機構失控，因此在設計和應用時應該盡量避開其奇異位形［3-4］。

即:

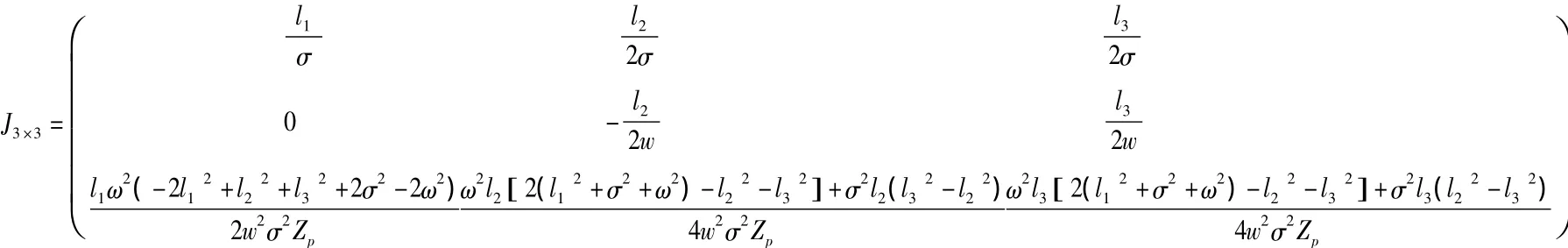
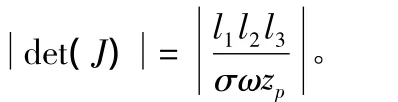
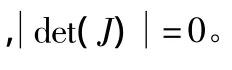
3 平穩性研究

三階逆雅可比矩陣為:

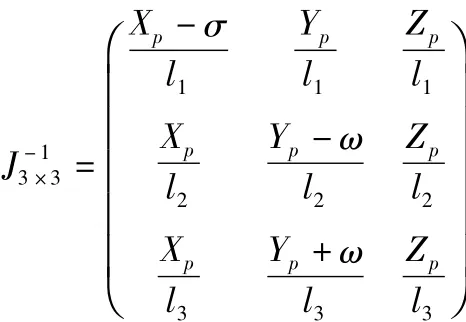
以基坐標系o－xyz為參考系，動平臺坐標系原點P在基坐標系o－xyz中坐標為（xp，yp，zp），假設P點在Z=950 mm截面內做圓周運動，其運動方程為:

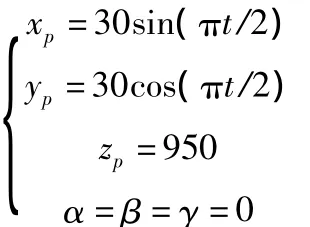
其中t的單位為s，xp，yp，zp單位為 mm。其他結構參數如下:靜平臺半徑R=1 000 mm，動平臺半徑D=350 mm，驅動桿桿長lmin=900 mm，lmax=1 900 mm。利用 MATLAB進行數據處理，得到桿和動平臺線速度和線加速度曲線。其中圖4為各桿的速度;圖5為各桿加速度;圖6為動平臺速度;圖7為動平臺加速度。

圖4 各桿的伸縮速度

由圖4～圖7可知:桿1最大線速度為31.387 mm/s，最大線加速度為49.303 mm/s2;桿2最大線速度為28.894 mm/s，最大線加速度為45.387 mm/s2;桿3最大線速度為28.895 mm/s，最大線加速度為45.39 mm/s2，曲線沿 x 軸呈正余弦變化。動平臺中心點最大線速度為47.122 mm/s，理論值為47.124 mm/s，最大線加速度為74.021 mm/s2，理論值為74.022 mm/s2。該機床驅動桿的伸縮速度曲線連續并且非常光滑，說明該機床運動時的平穩性較好。

4 結束語

［1］王傳強，趙恒華.3-TPT并聯機床奇異性及平穩性研究［J］.組合機床與自動化加工技術，2010，（10）:26-28.

［2］劉素明，趙強，李軍.3-2HSS并聯機床運動學分析及運動仿真［J］.機床與液壓，2008，（9）:115-117.

［3］陳旭，鄧亮，蔡光起，等.基于3-UPS機構并聯機床的運動學分析［J］.機械與電子，2005，（6）:9-11.

［4］王傳強，趙恒華.并聯機床的奇異性研究［J］.石油化工高等學校學報，2010，（6）:84-88.