基于相對貼近度的不確定多屬性決策法及其在人才引進中的應用

屈文閣

(陜西理工學院人事處，陜西漢中723000)

由于客觀事物的復雜性和不確定性，以及決策者的積極參與，對方案有偏好信息的不確定多屬性決策問題已成為現代決策科學中的一個研究熱點[1-9］。目前，一些學者對此進行了研究并提出了一些方法。如文獻[1-2］研究了屬性權重未知、屬性值和偏好信息均以區間數效用值形式給出的不確定多屬性決策問題，分別提出了最小偏差法與線性規劃法;文獻[3-4］研究權重信息部分確知、偏好信息分別為區間數互反和互補矩陣判斷的不確定多屬性決策問題。分別提出了基于區間數正理想點及其投影的方案排序法[3］和基于C-OWA算子的決策方法[4］。文獻[5］針對屬性值以區間數形式給出并且已知方案偏好信息的多屬性決策問題，提出了一種灰色關聯分析的決策方法。文獻[6］研究了方案偏好信息以區間數互反判斷矩陣形式給出，屬性偏好信息以區間數互補判斷矩陣形式給出的不確定多屬性決策問題。基于區間判斷矩陣的一致性建立目標規劃模型獲得權重，并將區間屬性值數值化進行排序，存在信息損失。文獻[7］研究了權重信息為區間數、屬性值為直覺模糊數且決策者對方案的偏好信息以直覺判斷矩陣形式給出的模糊多屬性決策問題。提出了基于線性規劃和得分矩陣的決策方法。文獻[8－9］基于直覺模糊集理論研究了對方案有偏好的不確定多屬性決策問題，利用區間直覺模糊有序加權算術與幾何平均算子對信息進行集結，利用得分函數和精確函數對方案進行排序。本研究在上述文獻的基礎上，針對權重信息部分確知且對方案有偏好的不確定多屬性決策問題。基于主觀偏好信息，建立一個目標規劃模型，通過求解該模型得到屬性權重，進而獲得加權規范化矩陣。對TOPSIS法進行改進，并利用相對貼近度方案進行排序或擇優。最后，將方法應用于人才引進問題驗證了方法的可行性和有效性。

1 問題描述及決策矩陣的規范化

權重信息部分確知且對方案有偏好信息的不確定多屬性決策問題的基本模型可以描述為:設X={x1，x2，…，xn}為方案集，S={s1，s2，…，sm}為屬性集，ω =(ω1，ω2，…，ωm)T為權重向量，并設 Φ ={ω =(ω1，ω2，…，ωm)T，ω∈為已知的部分權重信息所確定的可能權重集合。記 M={1，2，…，m}，N={1，2，…，n}，則 i∈M，j∈N。決策者對方案 xj∈x的主觀偏好信息為對于方案xj，按第i個屬性si進行測量得到xj關于si的屬性值為區間數從而構成屬性決策矩陣，最常見的屬性類型一般分為效益型和成本型。效益型是指越大越好的屬性;成本型是指越小越好的屬性。設I1、I2分別表示效益型、成本型下標集合，易知M=I1∪I2。

一般而言，不同的評價屬性往往具有不同的物理量綱和量綱單位，為了消除不同量綱和量綱單位帶來的不可公度性，決策之前應將屬性進行無量綱和規范化處理。為此，根據評價屬性的類型，按公式(1)、(2)把屬性決策矩陣轉為規范化[1］矩陣，其中，且

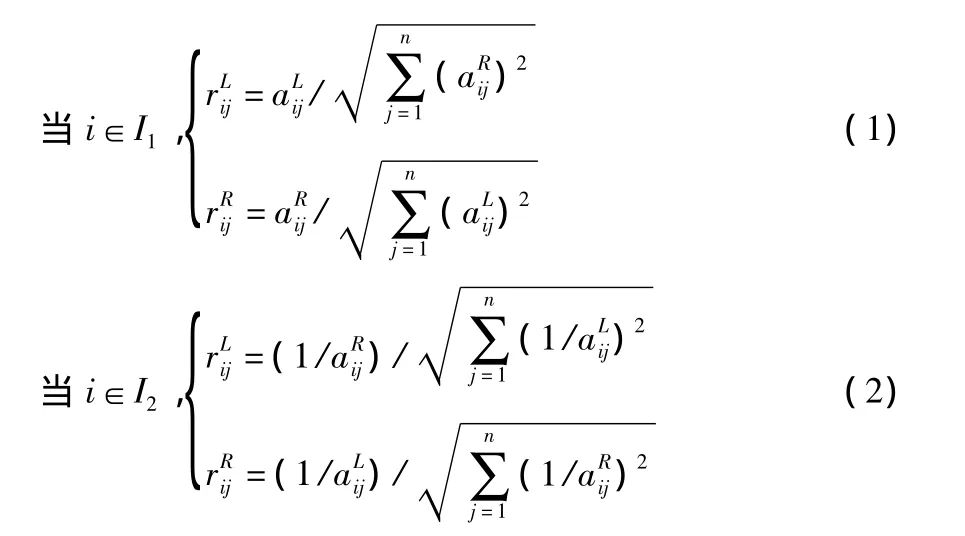
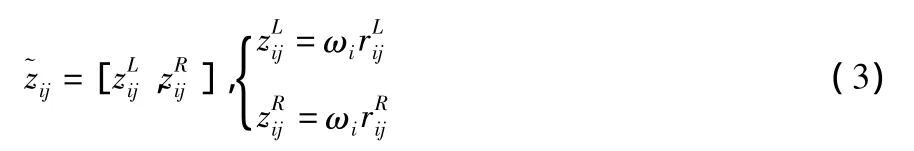
2 決策方法

定義[1］1 設區間數，稱為區間數與的距離。

由于屬性權重不完全確知，我們需先確定屬性權重以便對方案排序。考慮決策信息與決策者的偏好一致化，且各決策方案之間是公平競爭的。為此，建立下列目標規劃模型:

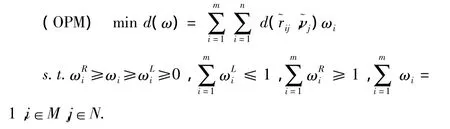
利用LINGO軟件求解上述模型獲得屬性權重ω并代入(3)式，即可得到加權屬性矩陣

為了對方案進行排序，首先，給出下列定義:

定義[4］2 如果記，且

其次，計算第j方案與正理想解和負理想解的投影:

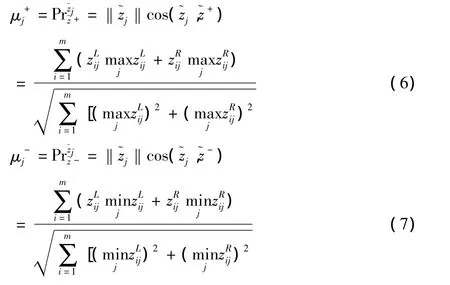
最后，計算各方案的相對貼近度:

由于理想解和負理想解事實上不一定存在。易知，方案的優劣的排序即為λj由大到小的排序。

基于上述討論，下面通過某高校人才引進的決策問題，給出求解步驟并說明模型及排序方法的有效性。

3 算例

高校人才引進是一個多因素的決策問題，決策者一方面要把德才優秀的人才引進，另一方面，也希望在條件相當的情況下引進自己所偏愛的人才。假設某高校制定的考核主要指標(屬性)為:人力成本(s1);知識結構和創新能力(s2);思想品德(s3);后期培養費(s4)。顯然，s2與s3為效益性屬性，s1與s4為成本型屬性。現有4名候選人xj(j=1，2，3，4)，決策者對每位候選人各指標進行打分，經過數據處理候，選人的屬性值及屬性權重信息列于表1:

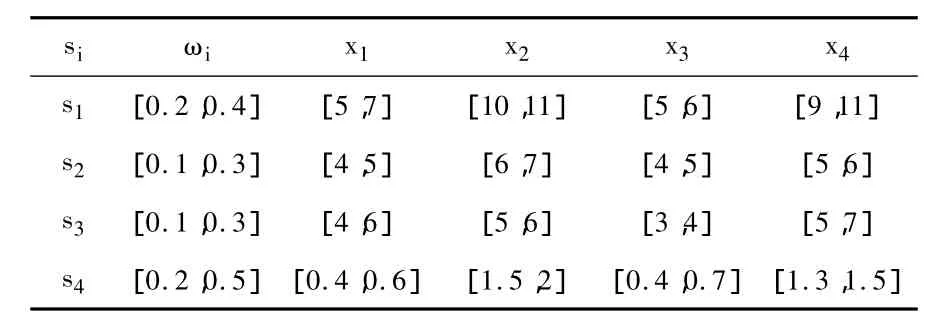
表1 原始決策矩陣和權重信息Tab.1 Original decision-making matrices and weighting information

Setp1利用公式(1)、(2)，由表1可得到規范化決策矩陣如下:

Step2利用模型(OPM)，求解得屬性權重向量為:ω=(0.32，0.15，0.35，0.18)T，從而由(3)式可得加權的規范化決策矩陣:

Step3由(4)、(5)式確定理想解和負理想解為:

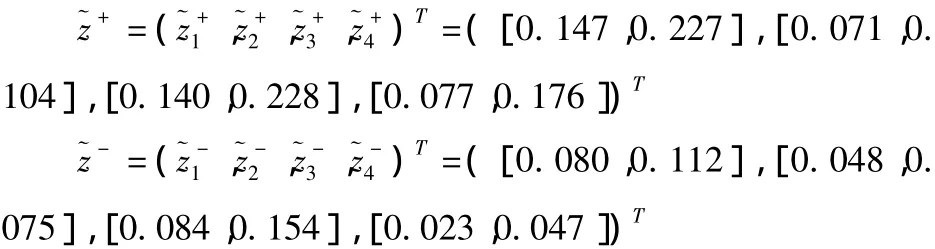
由(6)、(7)、(8)式可計算解得相對貼進度為:λ1=0.531 7;λ2=0.037 4;λ3=0.276 5;λ4=0.912 2。從而 4位候選人的優先為x4＞x1＞x3＞x2，故首先考慮引進x4作為最佳選擇。

4 結束語

本研究針對權重信息部分確知且對方案有主觀偏好信息的不確定多屬性決策問題，提出一種基于目標規劃和相對貼進度的決策方法并應用于人才評價中。該方法不僅能充分利用主客觀信息，最大限度地體現決策者的主觀愿望，使得決策結果更具合理性。而且算例表明該方法具有計算簡單易于上機實現的優點，從而為求解不確定性的多屬性決策問題提供了一條新途徑。

[1]徐澤水.不確定多屬性決策方法及應用[M］.北京:清華大學出版社，2004.

[2]姜艷萍，樊治平.給出方案偏好信息的區間數多指標決策方法[J］.系統工程與電子技術，2005，27(2):250—252.

[3]Xu ZS.On method for uncertain multiple attribute decision making problems with uncertain multi-plicative preference information on alternatives[J］.Fuzzy Optimization and Decision Making，2005，4(2):131—139.

[4]Zhou HA，Liu SY，Fang XR.Method for uncertain multi-attribute decision making with preference information in the form of interval numbers complementary judgment matrix[J］.Journal of Systems Engineering and Electronics，2007，18(2):265—269.

[5]衛貴武，魏宇.對方案有偏好的區間數多屬性灰色關聯決策模型[J］.中國管理科學，2008，16(1):255—261.

[6]馮向前，魏翠萍，錢曉華.基于偏好信息一致性程度最大的多屬性決策方法[J］.運籌與管理，2012，19(4):73—77.

[7]徐澤水.直覺模糊偏好信息下的多屬性決策途徑[J］.系統工程理論與實踐，2007，27(11):62—71.

[8]衛貴武.對方案有偏好的區間直覺模糊多屬性決策方法[J］.系統工程與電子技術，2009，31(1):116—120.

[9]夏梅梅，魏翠萍.對方案有偏好的直覺模糊多屬性決策方法[J］.計算機工程與應用，2009，45(2):137—139.