地基GPS傾斜路徑水汽計算方法研究＊

朱 爽

（中國地震局第一監測中心，天津300180）

0 引 言

地基GPS水汽探測技術可以利用GPS觀測數據計算出高精度的可降水汽量PWV，精度可以達到1～2mm［1］．但PWV是指測站上空天頂方向上總的水汽含量，它所反映的是測站上空一段時間內所有GPS傳播路徑上的一維平均水汽，并不能提供水汽的三維分布信息，這在某種程度上影響了地基GPS在數值天氣預報上的應用［1］。Davis等人（1993）研究發現:當站點上空30°仰角時，利用微波輻射計觀測得到的水汽分布信息在不同方位上會有20%的變化［2］。一維的PWV是不能給出水汽的這種空間變化的，這促進了GPS信號斜路徑方向上的水汽總量（SWV）的發展。Ware等人［3］首先開始了應用GPS觀測斜路徑延遲STD的研究工作，利用雙差法證明了GPS觀測斜路徑延遲STD 的可行性［3］；Alber等人 提出了一種從雙差殘差中獲得信號路徑上相位延遲的方法［4］，加快了這方面的研究進展；宋淑麗等人使用了一種直接計算SWV的方法［5］，認為其觀測精度在mm量級。SWV在氣象領域的應用研究也相繼開展，研究證實，把SWV同化到數值天氣預報模式的初始場中，即可以重構水汽的三維分布場，這對數值天氣預報具有重要的意義［6］。MacDonald利用3D VAR方法從SWV觀測值中獲得了水汽的三維分布，并進行與中尺度天氣數值模式水汽場的對比分析［7］，實驗證明較高分辨率的GPS接收機可以進行水氣的三維層析。

介紹了利用GPS進行傾斜路徑水汽含量計算的方法，同時介紹了利用微波輻射計WVR計算傾斜路徑水汽含量的原理，在此基礎之上，利用GPS與微波輻射計WVR的并址觀測站2002年5月26日的觀測數據進行實驗，將實驗結果進行對比。對比結果顯示，利用地基GPS可以實現傾斜路徑上可降水汽量（SWV）的計算，其與WVR觀測值的偏差平均值為1．83mm，均方根誤差為4．23mm．實驗同時證明:傾斜路徑水汽含量與衛星高度角有很強的關系，高度角較低時，誤差較大，高度角較低時，誤差較小。

1 傾斜路徑水汽含量的計算方法

在高精度GPS數據處理中，通常把對流層延遲表示為天頂方向的延遲量ZTD與高度角有關的映射函數M（E）之積，而天頂方向的總延遲量（ZTD）分為天頂干延遲 （ZHD）和天頂濕延遲（ZWD）之和，且對于天頂干延遲和天頂濕延遲采用不同的映射函數，為

ΔDtrop＝ZTD·M（E）

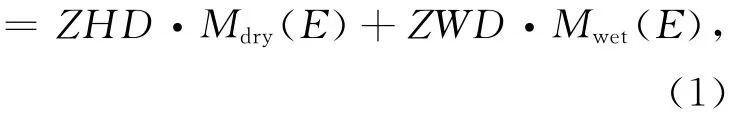
式中，Mdry（E）和Mwet（E）分別為天頂干、濕延遲的映射函數。

獲得天頂濕延遲后，即可由式（2）得出天頂方向可降水汽量

其中，∏為無量綱水汽轉換系數，它的表達式為

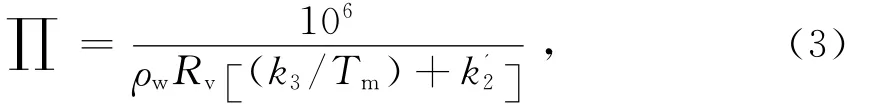
式中:Rv為氣體常數；k＇2和k3分別為大氣折射常數；Tm為大氣加權平均溫度。

而當GPS衛星信號在經過對流層大氣時，信號是沿著傾斜路徑進行傳播的。傾斜路徑方向上的濕延遲為接收機至衛星之間濕折射率的積分［4］。

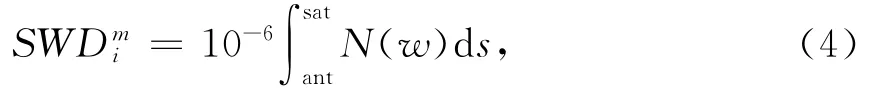
式中:SWDmi為傾斜路徑上測站i與衛星m 之間的濕延遲；ant代表 GPS接收機天線；sat代表GPS衛星；s代表積分信號路徑，濕折射率N（w）為水汽分壓ew及溫度T的函數 :

式中，常數k＝3．73×105K2hpa－1．

傾斜路徑上的水汽總量SWV可由式（6）計算所得

式中，∏為前述計算PWV時所使用的無量綱比例因子。

一個SWD觀測值可以看作是兩部分之和，一個部分是各向同性部分，即天頂濕延遲量ZWD，它可以認為是一段觀測時間內一個測站到所有可見衛星的SWD觀測值映射到天頂方向后的平均值，天頂方向水汽含量PWV意味著水汽在一段時間內保持不變且是水平均勻的，但實際上這種情況并不總是正確的，在發生強對流、臺風等天氣時，水汽場的空間變化十分復雜，顯然PWV不能給出這種空間變化信息。第二個部分是各向異性部分，即斜路徑延遲對各向同性成分ZWD的偏離，這一項即是不同方位角上的差異［8－9］。

由上分析可知，斜路徑延遲水量SWV由各向同性部分PWV和各向異性部分組成。PWV代表了大氣在天頂方向上的平均值，各向異性可以認為是SWV在天頂方向上的偏離。其中，各向異性成分又包括了水平梯度項和觀測值相位殘差兩項。基于以上分析，可以得出STD的計算公式:

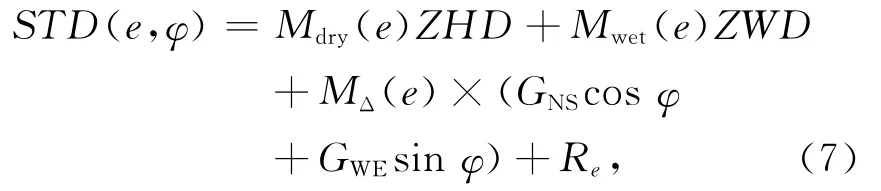
式中:e為衛星高度角；φ為衛星方位角；Mdry（e）為干映射函數；Mwet（e）為濕映射函數；MΔ（e）為水平梯度映射函數；GNS為南北方向的水平梯度，GWE為東西方向的水平梯度；Re為傾斜路徑的相位殘差。在GAMIT中，

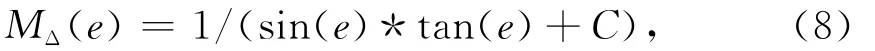
式中，C＝0．003 2．

則SWV的計算公式:

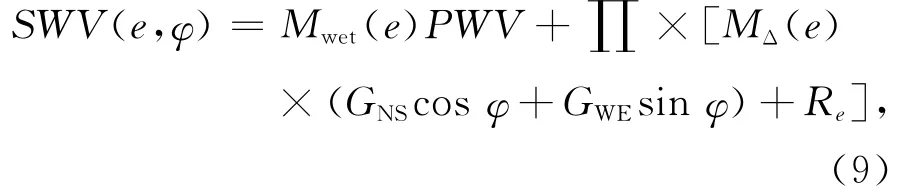
在高精度GPS數據處理中，常采用的計算對流層參數的方法有非差精密單點定位法（PPP）和雙差法，在有遠距離測站參與解算時，PPP和雙差法的精度相當。基于PPP的方法具有估計模型簡單、無需引入遠距離參考站、實時快速的特點，美國的GIPSY和德國的EPOS軟件都是基于PPP進行參數估計。但是，基于精密單點定位時，高精度鐘差的獲取使得它較難獲得高精度的估計結果。而在雙差法中，接收機鐘差及衛星鐘差都通過雙差法消除，并且可以準確地獲得整周模糊度，GAMIT軟件和瑞士伯爾尼大學的BERNESE軟件都采用雙差法進行參數估計。以GAMIT為基礎進行斜路徑延遲的估算。

2 微波輻射計WVR計算SWV的原理

WVR微波輻射計是觀測大氣信息的一種儀器，它可以借助微波輻射傳輸方程觀測天空亮溫，從而反演傾斜路徑上的濕延遲量SWD和水汽總量SWV．它可連續跟蹤單顆GPS衛星，大約5～10min完成一組觀測。WVR可以探測天空的輻射，然后輸出天空亮溫，正比于天空亮溫的數字信號及觀測方向上的光學厚度。其傳輸方程為

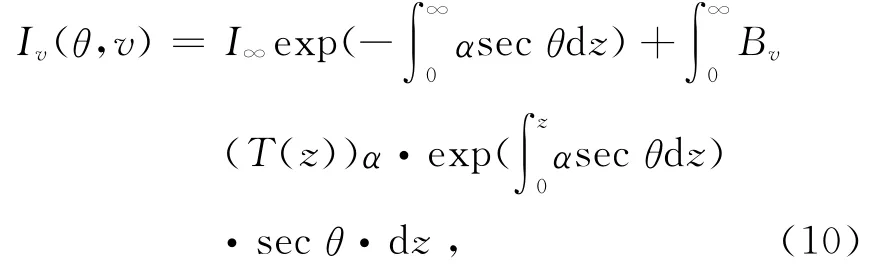
式中:I∞為宇宙背景的微波輻射強度；θ為天頂角；v為頻度；T（z）為溫度廓線；Bv（T（z））為黑體輻射強度；α為吸收系數，由水汽分子、云中液水和氧氣分子吸收系數三項構成。式（10）即為大氣中微波傳輸的基本方程。

通常情況下，選用不同的兩個通道頻率，一般為22．2GHz和35．3GHz，從地面和探空數據可以計算地面接收到的輻射，對應每一個探空曲線，可以得到兩個波段上的不同亮溫。結合亮溫、平方項、地面氣壓、濕度等，進行逐步回歸，即可以得到水汽總量L的反演方程為

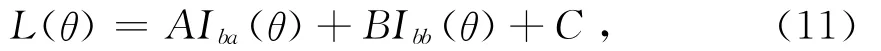
式中:A，B，C為回歸系數，根據不同地點的具體情況設定；θ為天頂角。

WVR觀測得到的延遲信息精度較高，可以達到5mm，通常作為GPS斜路徑水汽信息的對照信息。需要注意的是，在大氣水汽含量較高或者正在降雨時，WVR的觀測結果是不可靠的。所選擇WVR觀測所得的延遲信息進行對比，用來檢驗GPS斜路徑水汽計算的正確性。

3 傾斜路徑水汽SWV的解算結果驗證

3．1 數據說明

選用了卡爾加里大學提供的GPS、微波輻射計WVR的并址站uofc站2002年5月26日（年積日第146天）的數據進行實驗。

利用GAMIT軟件進行數據處理時，為了獲取精度較高的水汽計算結果，加入了9個IGS觀測站，分別為 ALGO，AMC2，DRAO，DUBO，FLIN，PIE1，PRDS，SHAO，YELL．

其中，GAMIT的解算策略如下:星歷采用廣播星歷，截止高度角為10°，基線處理模式為RELAX（松馳解），電離層延遲模型為LC－HELP，對流層模型為Saastamoinen模型，映射函數為NMF模型，測站坐標約束為0．010m，每1h估計一次對流層參數。

3．2 驗證結果分析

利用GAMIT計算得到的天頂方向水汽量PWV與WVR提供的結果進行對比。由于WVR提供的值為每個時刻對單顆衛星的觀測結果，因此將10min內的所有觀測值取平均，得到每隔10 min的天頂可降水汽量。另外，GAMIT得到的原始結果是每1h獲取一個PWV，將間隔為1h的數據內插為每隔10min一次的數據進行對比。圖1示出了對比結果。

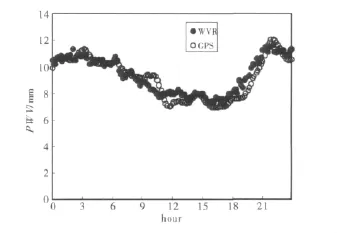
圖1 利用GPS與WVR得到的PWV對比圖

由圖1可以看出，通過GPS數據解算的PWV結果與WVR提供的結果變化趨勢一致，誤差較小。在此基礎之上，對兩者的結果進行了統計分析，偏差的平均值為1．17mm，均方根誤差為1．75 mm．本結果與國際上PWV的計算誤差1～2mm的精度相當，也為后續的SWV對比提供了可靠的PWV值。

選取了第146日UOFC站上25、21、14、18號衛星的GPS、WVR觀測結果進行對比，由于WVR對單顆衛星的觀測時間間隔約為8min，而GPS對單顆衛星的觀測時間間隔為30min，按照WVR的觀測時刻選取了GPS相應觀測時刻的值來進行對比。結果如圖2所示。

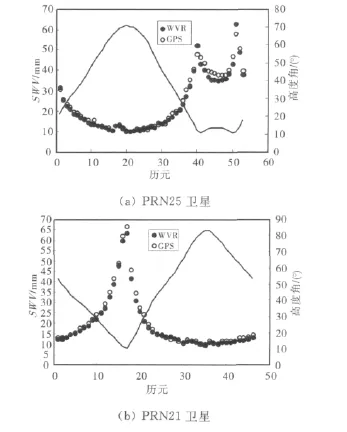
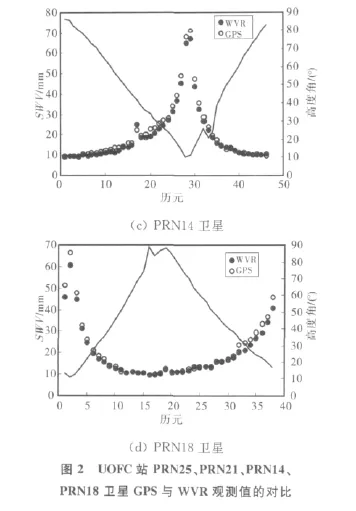
由圖2可明顯看出，隨著高度角的降低，GPS與WVR獲得的SWV都逐漸增大，兩者的變化趨勢一致。在高度角較高時，兩者的值都較小，這時因為高度角較高，傾斜路徑幾乎等于垂直路徑，斜路徑延遲中的各向異性部分較小，SWV與PWV的值相近；高度角降低，SWV逐漸增大，這是因為高度角較低，斜路徑與垂直路徑偏差較大，各向異性部分增大，導致SWV與PWV的偏差較大。另外，將基于GPS與WVR的SWV偏差進行對比，如圖3所示。

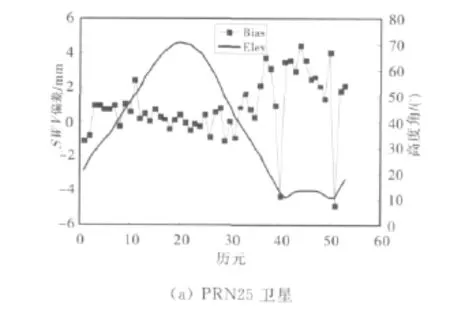
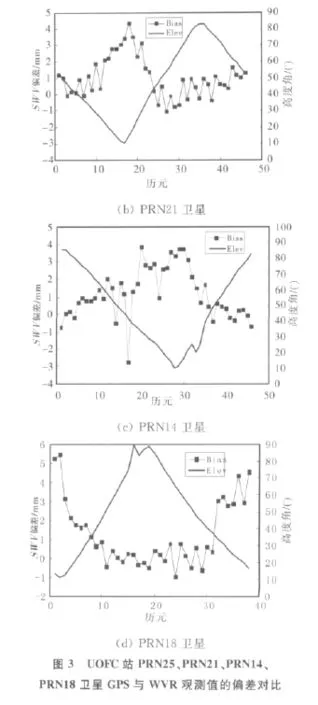
由圖3可以看出，高度角較高時，兩者的誤差較小，一般在－1與1mm之間；高度角變低時，兩者的誤差較大，高達6mm．這是因為在高度角較低時，SWV的各向異性成分變大，估計過程中由于非差殘差和多路徑效應及其它非模型化的誤差難以準確得到，導致低高度角時SWV的估計誤差變大。

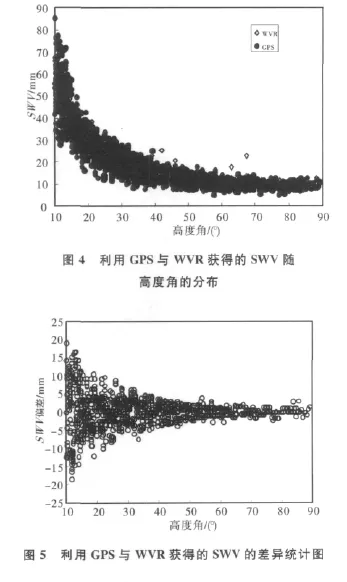
圖4是UOFC站第146日所有觀測時刻GPS與WVR所得的SWV隨高度角的分布圖。圖5是兩者的差值統計圖。

由圖4、5可以明顯看出，隨著高度角的增大，SWV的值逐漸減小，這與圖2的情況相符合；同時，隨著高度角的增大，利用GPS與WVR獲得的SWV差值也逐漸減小，這與圖3情況相符合。同時也證明了前文中的分析是正確的。統計了該天所有觀測數據的差值，差值平均值為1．83mm，均方根誤差為4．23mm．綜合以上分析可以得知，利用GPS觀測數據，采用雙差法可以計算出精度較高的SWV．

值得一提的是，當高度角較低時，GPS與SWV的誤差較大，這是由于在低高度角時，SWV的各向異性成分較大，利用GPS估計各向異性成分的過程中產生較大誤差。在數據處理中，要先確定PWV準確的獲得，在此基礎之上，進行各向異性成分的計算；在計算過程中，要減少多路徑效應的影響，同時，可以改進在非差殘差獲得過程中的定權方式，比如采用根據高度角定權，另外還要考慮殘余的未模型化的大氣延遲。由于數據有限，還需進行更深入的研究。

4 結 論

一維的PWV是天頂方向上的水汽含量，不能全面反映水汽的分布信息，而SWV是傾斜路徑上的水汽含量，它包括各向同性部分，即天頂方向上的PWV，以及各向異性部分。由于SWV可以反映水汽在不同方位上的分布，對于研究水汽的三維層析及時空變化具有重要意義。利用GPS觀測數據獲得了傾斜路徑上的SWV，并與WVR提供的數據進行對比，結果表明，兩者的差值平均值為1．83mm，均方根誤差為4．23mm．實驗分析還得出，傾斜路徑上的SWV與高度角存在很大的相關性，高度角較低時，SWV的值明顯增大，這是由于低高度角時SWV的各向異性成分明顯增大；而高底角較高時，SWV的值與PWV的值相差不大，估計精度也較高。

［1］ 畢研盟．應用全球定位系統（GPS）遙感大氣水汽的研究［D］．北京:北京大學，2006．

［2］ DEVIS J，ELGERED G，NIELL A，et al．Groundbased measurement of gradients in the"wet"radio refractivity of air［J］．Radio Sci．1993，28（6）:1003－1018．

［3］ WARE R，ALBER C，ROCKEN C，et al．Sensing integrated water vapor along GPS ray paths．Geophys［J］．Res．Lett．，1997（24）:417－420．

［4］ ALBER C，WARE R，ROCKEN C，et al．Obtaining single path phase delays from GPS double differences．Geophys［J］．Res．Lett．，2000（27）:2661－2664．

［5］ 宋淑麗，朱文耀，程宗頤，等．GPS信號斜路徑方向水汽含量的計算方法［J］．天文學報，2004，45（3），338－346．

［6］ GUO Y R，KUO Y H，DUDHIA J，et al．Four－dimensional variational data assimilation of heterogeneous mesosacle observations for a strong convective case．［J］．Mon．Wea Rev，2000（128）:619－643．

［7］ MACDONALD A E．XIE Yuanfu，WARE R H．Diagnosis of three－dimensional water vapor using slant observations from a GPS network［J］．Mon．Wea Rev．2002，130 （2），386－397．

［8］ 宋淑麗．地基GPS網對水汽三維分布的監測及其在氣象學中的應用［D］．上海:中國科學院研究生院，2004．

［9］ 張雙成．地基GPS遙感水汽空間分布技術及其應用的研究［D］．武漢:武漢大學，2009．