徑向基函數神經網絡在衛星鐘差預報中的應用＊

雷 雨，趙丹寧

（1．中國科學院國家授時中心，陜西 西安710600；2．中國科學院時間頻率基準重點實驗室，陜西 西安710600；3．中國科學院精密導航定位與定時技術重點實驗室，陜西 西安710600；4．中國科學院，北京100049）

0 引 言

衛星鐘差的精度直接影響著全球衛星導航系統（GNSS）的導航定位結果，主要體現在以下兩個方面:首先，衛星鐘差參數通過導航電文發播，任意時刻的鐘差是通過外推得到的，其預報精度直接決定了導航定位的精度［1］；其次，在實時精密單點定位（PPP）中，為了達到厘米級的定位精度，需采用預報鐘差參與解算［2］。因此，提高衛星鐘差的預報精度具有重要意義。

較常用的鐘差預報模型為多項式模型和灰色模型，許多學者對其進行了研究，并取得了顯著的效果［3－4］。但這兩種模型都存在一定的局限性:多項式模型的預報精度會隨著預報時間的延長而降低［4］，此外，該方法易受多項式擬合階數等人為因素的影響；而灰色模型對鐘差數據類型有較強的依賴性，要求鐘差數據平滑且呈指數規律變化，限制了其應用范圍［5］。近年來，國內外學者又發展了多種鐘差預報模型［6－7］，其中神經網絡（NN）由于具有通過學習訓練以任意精度逼近任意連續函數的能力，在鐘差預報中取得了良好的效果［8－10］。李孝輝等首次將誤差反向傳播（BP）神經網絡應用于原子鐘鐘差預報中，研究表明神經網絡比AR模型的預報精度高，且鐘差異常值對BP神經網絡模型預報性能的影響較小；郭承軍等將徑向基函數（RBF）神經網絡應用于衛星鐘差預報中，研究表明:神經網絡比灰色模型具有更好的預報精度和穩定性；王威等采用RBF神經網絡的變型—廣義回歸神經網絡（GRNN）對衛星鐘差進行建模并預報，從輸入維數。光滑因子等幾個方面對預報性能的影響進行了較為系統的研究，結果表明GRNN預報模型優于傳統的二次多項式模型。應用RBF神經網絡進行衛星鐘差預報，由于神經網絡易學習過度，從而影響網絡的泛化（預報）能力，因而采用交叉驗證法（CV）優化網絡，并利用數值試驗討論了該方法的預報精度。

1 RBF神經網絡

1985年，Powell提出了多變量插值的徑向基函數方法。1988年，Moody和Darken提出了一種神經網絡結構，即RBF神經網絡，它能夠以任意精度逼近任意連續函數，與BP神經網絡相比，RBF神經網絡具有學習速度快、全局收斂等優點。

1．1 RBF神經網絡的結構

RBF神經網絡是一種三層前饋式神經網絡，包括一個輸入層、一個隱含層和一個輸出層。輸入層由信號源結點組成；第二層為隱含層，隱含層神經元數目視所描述問題的需要而定，隱含層神經元的傳遞函數是對中心點徑向對稱且衰減的非負非線性函數；第三層為輸出層，它對輸入模式的作用做出響應。從輸入空間到隱含層空間的變換是非線性的，而從隱含層空間到輸出層空間的變換是線性的。

RBF網絡的基本思想是:以徑向基函數作為隱含層神經元的基構成隱含層空間，這樣就可以將輸入矢量直接映射到隱含層空間，而不像BP網絡那樣需要權連接，當RBF的中心點確定以后，這種映射關系也就確定了。而隱含層空間到輸出空間的映射是線性的，即網絡的輸出是隱含層神經元輸出的線性加權和，此處的權即為網絡可調參數。由此可見，從總體上看，網絡由輸入到輸出的映射是非線性的，而網絡輸出對可調參數而言卻又是線性的。這樣網絡的權就可以由線性方程直接解出，從而大大加快學習速度并避免局部極小問題。

RBF網絡的關鍵在于隱含層節點徑向基函數的非線性逼近性能，徑向基函數表現為多種形式，常見的為高斯函數，其形式如下:

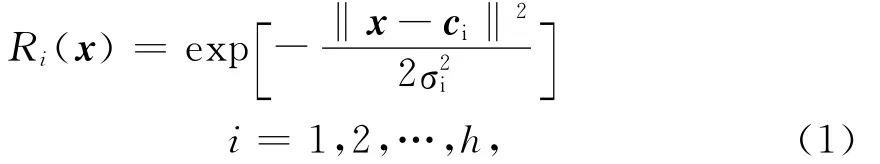
式中:x為輸入向量；ci為隱含層第i個節點的中心向量，與x同維；σi表示高斯函數的寬度；‖xci‖為向量x－ci的歐式范數；h表示隱含層神經元的個數。

輸出層節點相應的輸出可表示為

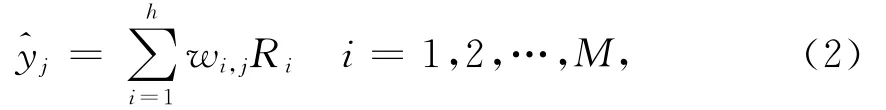
式中:＾yj為第j個輸出單元的輸出值；M表示輸出層神經元的個數；wi，j為第i個隱單元到第j個輸出單元的權值。

1．2 RBF神經網絡的學習算法

通常，RBF網絡的學習分為2個階段進行，即隱含層的學習和輸出層的學習2步。

1）隱含層學習

隱含層學習表現在隱含層神經元的數目h、中心向量c和高斯函數的寬度σ的確定上。其中，隱含層神經元數目的確定是關鍵問題，傳統的做法是使其與訓練集樣本數目相同；而中心可根據訓練樣本點在自變量空間的分布，選出或計算出有“代表性“的點作為中心點，再由中心周圍的樣本點確定寬度σ，應用較多的為聚類分析法。

2）輸出層學習

輸出層學習體現在隱含層與輸出層間的連接權w的確定上，可以應用最小二乘法對網絡輸出權值進行訓練，其學習訓練的目標是使總誤差達到最小。

1．3 RBF神經網絡的MATLAB工具箱函數

1）RBF神經網絡創建函數

MATLAB函數newrbe用于創建一個精確的RBF神經網絡，其調用格式如下:

net＝newrbe（P，T，spread），

其中，P為網絡的輸入向量；T為網絡目標向量（輸出向量）；spread為徑向基函數的寬度σ（默認為1．0）；net為創建好的RBF網絡。

在MATLAB中，沒有專門的RBF神經網絡訓練和學習函數，這是因為在使用函數newrbe創建RBF網絡的過程中，newrbe函數就根據訓練樣本P、T確定了網絡結構，即隱含層神經元數、權值和閾值等網絡參數。函數newrbe需要調節的參數只有一個spread，一般根據先驗知識選取。newrbe函數創建網絡的過程為

①隱層神經元數目等于輸入樣本數，其權值等于輸入向量的轉置:

式中:IW為隱層神經元的權值；PT為輸入向量P的轉置。

②設置隱層神經元的閾值為b

③以隱含層神經元的輸出作為輸出層神經元的輸入，確定輸出層神經元的權值和閾值，使之滿足:

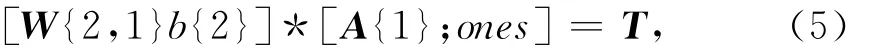
式中:W｛2，1｝、b｛2｝分別為輸出層神經元的權值和閾值；A｛1｝為隱含層神經元的輸出。

可以看出，上述過程只要進行一次就可以得到一個零誤差的徑向基網絡，所以以newrbe函數創建網絡的速度是比較快的，但由于隱層神經元數等于輸入樣本數，如果輸入向量數目很大時，將導致網絡的規模也很大。

2）RBF神經網絡仿真函數

函數sim用于利用已經創建好的RBF神經網絡進行仿真預測，其調用格式為

＾y＝sim（net，＾P），

其中，net為創建好的RBF網絡；＾P為網絡的輸入向量；＾y為網絡輸出向量。

2 交叉驗證法

神經網絡對訓練樣本的逼近稱為擬合，而對非訓練樣本的逼近稱為泛化（預報）。顯然，衡量一個網絡訓練好壞的標準不僅是要考察網絡的擬合能力，更要檢驗其泛化能力，即訓練神經網絡的最終目的是確保訓練好的網絡同時具有良好的擬合能力及泛化能力。一般情況下，訓練能力差時網絡的泛化能力也弱，并且在一定程度上隨著訓練能力的提高泛化能力也會隨之提高，但是這種趨勢有一個極限，達到此極限后，隨著訓練能力的提高，泛化能力反而下降，即出現所謂過適性或過擬合，也稱為過學習，此時網絡學習了過多的樣本細節而不能反映樣本所蘊含的內在規律。欠學習。過學習的網絡都屬于不成熟網絡，泛化能力會很差，實際中網絡往往是過擬合。從上述意義上講，網絡訓練過程中存在兩方面的問題:

1）神經網絡對訓練樣本有較強的依賴性，如何從有限的訓練樣本中挖掘更多的信息是網絡訓練好壞的關鍵；

2）在網絡訓練過程中要著重考察網絡的泛化能力，避免發生網絡過學習的狀態。

解決上述問題的一個有效方法是采用交叉驗證法優化網絡。交叉驗證法的基本思想是在某種意義下將學習集進行分組，一部分做為訓練集，另一部分做為驗證集，首先用訓練集對神經網絡進行訓練，再利用驗證集來測試訓練得到的模型，以此來做為評價網絡性能的指標。交叉驗證法的一種改進方法是 K 重交叉驗證法（K－fold Cross－Validation）［11］，其工作方式如下:假定有個 N 樣本，將其隨機均勻分成K份，輪流選擇其中K－1份作為訓練樣本對網絡進行訓練，剩余的1份作為驗證（其樣本個數為N／K）校本以檢驗網絡的泛化性能。網絡需要訓練K次，也就可以創建K個網絡，選擇泛化誤差最小時的網絡模型為最優模型，用均方根誤差（RMSE）來衡量泛化誤差:

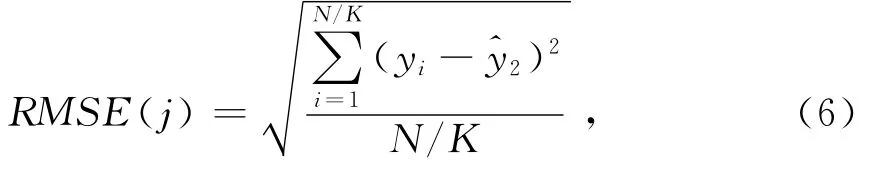
式中:RMSE（j）表示第j次訓練的網絡泛化誤差；j＝1，2，…，K；yi為理論值；＾yi為網絡輸出值。

3 基于RBF神經網絡的鐘差預報

3．1 利用RBF神經網絡進行鐘差預報的過程

利用RBF神經網絡方法進行鐘差預報的過程為:

1）確定網絡的輸入，輸出量及相應的維數。輸入量為已知的鐘差值，輸出量為鐘差預報值。

2）根據已知數據，進行學習集與測試集的分配。

3）數據的歸一化，由于各歷元鐘差數據相差懸殊，即輸入變量差異較大，為了使網絡訓練一開始就給各輸入分量以同等重要的地位，需要將輸入數據變換到同一范圍中。選用由MATLAB提供的premnmx函數，將輸入數據和與之對應的輸出數據進行歸一化處理，使處理后數據全部落在（－1，1）的范圍內，這樣有利于提高神經網絡的收斂速度，節省網絡訓練耗時，并且可以防止發生突變的鐘差數據對網絡訓練的影響。

premnmx函數的模型為

式中:p為需要歸一化的數據；pn為歸一化后的數據；minp、maxp分別表示p中的最大值和最小值。

4）網絡創建和訓練。采用MATLAB神經網絡工具箱函數newrbe建立RBF神經網絡，并根據學習集采用K重交叉驗證法優化網絡模型。

5）網絡仿真測試。利用訓練好的RBF神經網絡進行鐘差預報。

6）預報結果的逆歸一化處理，并對還原結果進行檢驗。

3．2 試驗結果與分析

為了分析RBF神經網絡模型預報衛星鐘差的精度，選取3顆鐘差變化較典型的衛星，分別是PRN03、PRN05和PRN08，其中PRN03呈遞增變化，PRN05呈遞減變化，而PRN08既呈遞增也呈遞減變化，具體的鐘差變化如圖4～6所示。采用的數據為2010年11月28日至30日的IGS事后GPS精密鐘差，采樣間隔為5min．由于灰色模型的鐘差預報效果優于二次多項式模型［3］，為了驗證RBF網絡的效果，采用灰色模型GM（1，1）對衛星鐘差預報，并將兩者加以比較。其中，3．2．1節給出了基于交叉驗證法的網絡訓練結果；3．2．2節將傳統灰色系統模型與RBF神經網絡模型的預報精度進行對比分析。

3．2．1 交叉驗證法試驗分析

算例中將28日和29日2天的數據作為學習集用于RBF神經網絡的學習訓練，將30日的數據作為測試集以檢驗模型效果，采用4重交叉驗證法將學習樣本隨機分成4份，其中3份作為訓練樣本，剩余1份作為驗證樣本，由于是用MATLAB函數newrbe實現RBF神經網絡的鐘差建模，因此每次訓練時需要調節的參數只一個spread，即徑向基函數的寬度σ，在（0．1，5）的范圍內選取，步長取0．1，對于每次訓練，驗證誤差（泛化誤差）最小時所對應的值即為最優值。只給出PRN08衛星的鐘差在訓練過程中訓練誤差（擬合誤差）和驗證誤差的變化情況，如圖1所示，其中橫坐標代表徑向基函數的寬度σ（spread），縱坐標代表均方根誤差（RMSE）。

由圖1可以看出，每次訓練的結果是訓練誤差幾乎相同，都不超過1ps，但驗證誤差卻不盡相同，這說明網絡的擬合能力與其泛化能力在某種程度上并沒有必然的聯系。為了更好、更直觀的反映網絡訓練效果，將圖1中的驗證誤差圖（圖1b）的部分區域放大作圖，放大后如圖2（a）、圖2（b）所示。另外，表1給出了每次訓練的最小驗證誤差。

結合圖1、2，分析表1，可以更清楚地看出:

1）spread對網絡性能有重要的影響。實際應用中，對于特定的衛星鐘差數據，spread值的調節過程有一定的規律，對于PRN08衛星鐘差數據，在一定的范圍內，spread值越大網絡性能越好，另外，每次訓練得到的最優spread值并不相同；

2）隨著訓練次數的增加，擬合誤差幾乎沒有變化，而驗證誤差則是先減小后增大，存在最小點，對應的最小值為0．211 4ns，出現在第2次訓練過程中，對應的擬合誤差和spread值分別為0．62 ps、2．4；

3）交叉驗證法通過多次訓練網絡能夠優化網絡模型，比只訓練一次的泛化誤差更小。

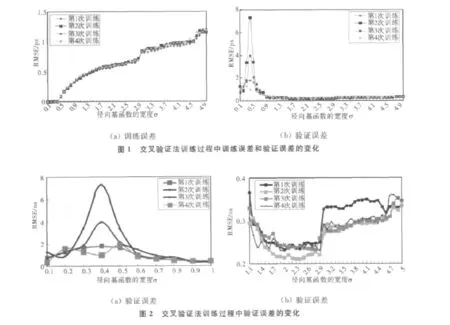
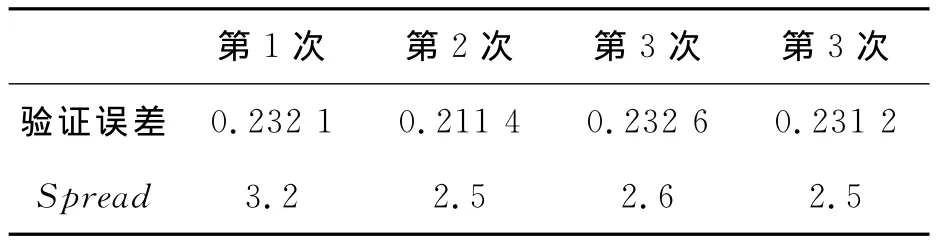
表1 驗證誤差／ns

為了驗證交叉驗證法的有效性，突出其優點，將其同常規方法（將學習樣本全部用來訓練網絡）進行對比，圖3示出了兩種方法對同一測試樣本的測試誤差。對于常規方法，測試誤差RMSE為17．30ns，而對于交叉驗證法，測試誤差RMSE僅為6．03ns，顯然，交叉驗證法可以明顯提高網絡的泛化能力。

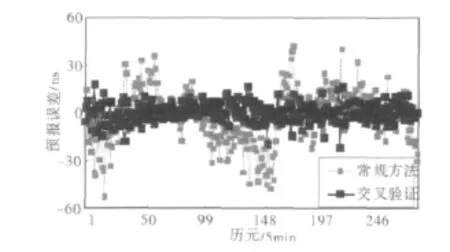
圖3 兩種方法的測試誤差

3．2．2 灰色系統模型與RBF神經網絡模型預報精度對比分析

分別利用灰色系統模型GM（1，1）和基于交叉驗證法的RBF神經網絡模型對3顆衛星的鐘差作24h的短期預報并進行誤差比較，如圖4～6所示。

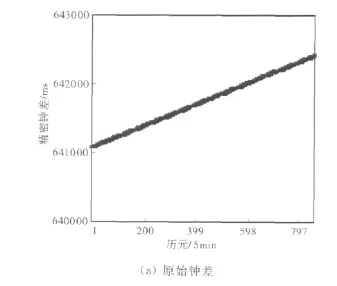
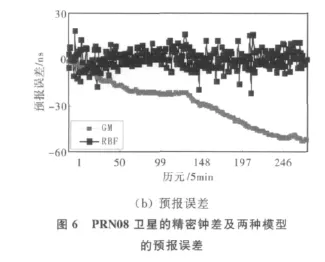
由圖4～6可以看出，傳統灰色模型對不同衛星鐘差在短期預報誤差異常波動很大，對鐘差數據類型有較強的依賴性，因此對于衛星鐘差短期預報而言，RBF神經網絡模型的預報精度和穩定性要明顯優于傳統灰色模型，可以在實際應用中來代替灰色模型。

為了進一步研究RBF神經網絡模型在衛星鐘差短期預報中的性能，對上述預報結果作誤差統計特性分析，如表2所示，其中MAX代表最大誤差，MEAN代表平均誤差，STD代表標準差。

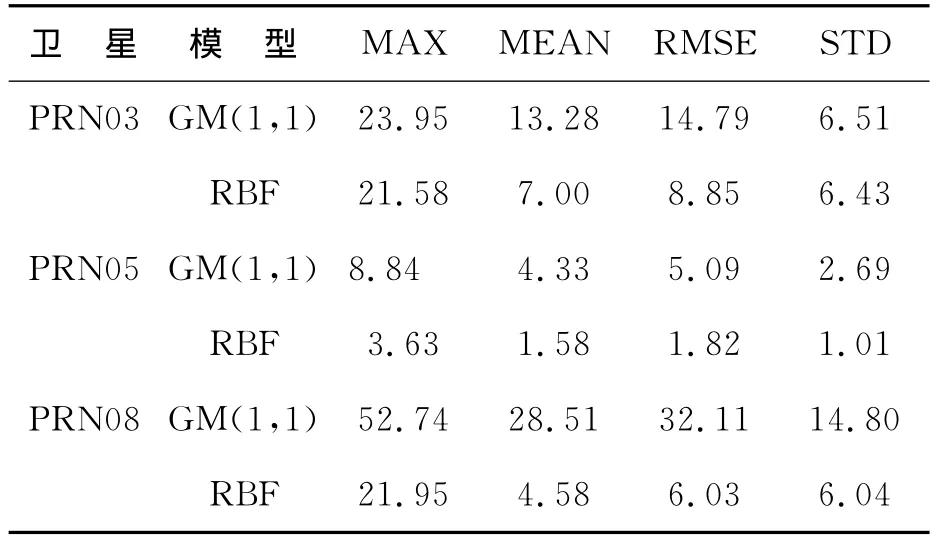
表2 預報誤差統計／ns

由表2可以更清楚地看出，對于衛星鐘差短期預報來講，RBF神經網絡模型較傳統灰色模型有更高的預報精度和更好的穩定性，然而RBF神經網絡模型也有一定的局限性，主要是對訓練樣本有一定的要求，體現在以下2個方面:

1）對訓練樣本的數量有一定要求，如果訓練樣本過少，網絡的學習效果就不是很好，相應地就會影響網絡的泛化能力，但訓練樣本也不能太多，過多的樣本將會導致過長的網絡訓練耗時；

2）要求訓練樣本數據具有一定的代表性，即能夠表征系統的變化特性，否則網絡的泛化能力也就不強。

4 結 論

通過以上對RBF神經網絡在衛星鐘差預報中的分析可以看出，RBF神經網絡模型較傳統的灰色系統模型在鐘差預報方面有一定的優勢，模型精度和穩定性均有所提高。在MATLAB環境下對RBF神經網絡建模，對參數要求較低，需要調節的只有一個徑向基函數的寬度參數，容易實現。但模型本身也有一定的局限性，對樣本數據依賴性強，且容易學習過度，對于后者，可采用交叉驗證法訓練網絡避免，試驗也表明該方法可以明顯提高網絡的泛化能力。另外，模型只適用于短期預報，如果要用于長期預報，則需要不斷增加新的樣本數據對模型進行再訓練。

僅僅對RBF神經網絡在衛星鐘差預報中應用的初步研究，所用方法尚需改進和完善，如何對模型進行優化以提高預報精度，以及如何將模型用于長期預報是下一步的研究重點。

［1］ 吳海濤，李孝輝，盧曉春，等．衛星導航系統時間基礎［M］．北京:科學出版社，2011．

［2］ 李 黎，匡翠林，朱建軍．基于IGU預報軌道實時估計精密衛星鐘差［J］．大地測量與地球動力學，2011，31（2）:111－116．

［3］ 崔先強，焦文海．灰色系統模型在衛星鐘差預報中的應用［J］．武漢大學學報·信息科學版，2005，30（5）:447－450．

［4］ 鄭作亞，盧秀山．幾種GPS衛星鐘差預報方法比較及精度分析［J］．山東科技大學·自然科學版，2008，27（4）:6－11，15．

［5］ 朱陵鳳，吳曉平，李 超，等．灰色模型在衛星鐘差預報鐘的缺陷分析［J］．宇航計測技術，2007，27（4）:34，42－44．

［6］ 朱祥維，肖 華，雍少為，等．衛星鐘差預報的Kalman算法及其性能分析［J］．宇航學報，2008，29（3）:966－970，1052．

［7］ 黃觀文，張 勤，許國昌．基于頻譜分析的IGS精密星歷衛星鐘差精度分析研究［J］．武漢大學學報·信息科學版，2008，33（5）:496－499．

［8］ 李孝輝，柯熙政．原子鐘信號的神經網絡模型［J］．陜西天文臺臺刊，2001，23（2）:110－115．

［9］ 郭承軍，滕云龍．基于小波分析和神經網絡的衛星鐘差預報性能分析［J］．天文學報，2010，51（4）:395－403．

［10］ 王 威，榮志飛，范國清．基于GRNN的導航衛星鐘差仿真方法研究［J］．系統仿真學報，2011，23（11）:2339－2345．

［11］ 丁常富，王 亮．基于交叉驗證法的BP神經網絡在汽輪機故障診斷中的應用［J］．電力科學與工程，2008，24（3）:31－34．