基于SiPESC平臺的拓撲優化模塊開發及應用

牛 飛， 梅 帥， 張 盛， 陳 飆 松， 程 耿 東

（大連理工大學 工業裝備結構分析國家重點實驗室，遼寧 大連 116024）

0 引 言

結構拓撲優化旨在尋求結構的最優拓撲形式，使得結構目標性能在滿足相關約束條件下達到最優.近30年來，拓撲優化研究得到了迅速發展，并在工業界得到廣泛的應用，已成為設計師在概念設計階段實現創新設計的有力工具［1］.

對于連續體結構的拓撲優化研究可追溯到1988年，Bendse等基于“微結構”思想提出了均勻化方法（homogenization method）［2］.之后，國內外學者們展開了豐富的相關研究，相繼提出了多種結構拓撲優化模型，如SIMP（solid isotropic material with penalization）方法［3］、進化法［4］、水平集方法［5］等.其中SIMP方法由于優化設計變量較少，優化求解實現簡單，備受學者和工程師們的青睞，從而得到了更為深入的研究和應用.

隨著結構拓撲優化技術在工程中的成功應用，近年來，幾乎所有的商用有限元軟件都在增加結構拓撲優化功能，比如MSC.Nastran、ANSYS等.與此同時，一些以結構拓撲優化為主要特色的商用軟件也相繼問世，如Altair公司的OptiStruct、FE－DESIGN公司的TOSCA、VR＆D公司的GENESIS以及Quint公司的OPTISHAPE－TS等［6］.無一例外，這些軟件的拓撲優化功能都是圍繞結構的剛度、頻率、應力等基本性能要求而開發，所采用的模型、算法也都是以往比較成熟的研究成果.但是隨著工程結構的性能需求日益多樣化，結構設計本身的復雜化，使得工程實際問題遠遠超出了優化軟件所能解決的范疇.受商用軟件本身封閉性和滯后性的制約，大量的學者針對復雜工程問題的新的研究成果不能及時在軟件中實施并應用到工程實際中.

另外，拓撲優化過程涉及結構響應分析和性能評價等問題，結構分析模塊是實現拓撲優化程序的一個重要環節.但是對于復雜問題（例如結構模型復雜、非線性問題等），開發結構分析程序需要投入大量的時間和精力，因此大多數學者的研究對象都是簡單的平面或實體單元，且結構模型規則.當然也有一些學者在商業軟件或開源有限元分析程序（ANSYS、Nastran、OpenSees等）上進行了一定的二次開發來研究復雜問題，然而這些商業CAE軟件均采用內嵌數據管理系統，其數據內部專用、接口不對外開放等特點依然給科研工作者帶來了大量的附加工作.

SiPESC［7］（software integration platform forengineering and scientific computation，工程與科學計算集成化軟件平臺）是由大連理工大學工業裝備結構分析國家重點實驗室研發的面向工程與科學計算的集成軟件系統.如圖1所示的體系結構，其所有應用功能均基于插件實現，具有可擴展、可維護、可重用、動態加載／卸載、使用靈活等優點.

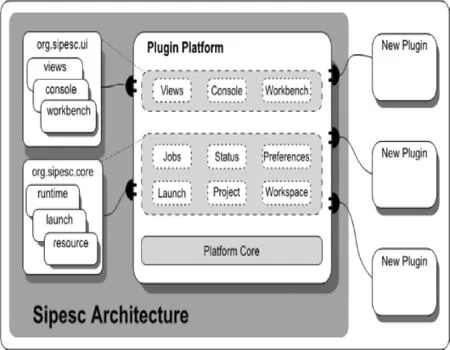
圖1 SiPESC軟件體系結構Fig.1 Software architecture of SiPESC

在開放接口的數據庫管理系統［7］以及基于此系統的結構分析系統 SiPESC.FEMS［7－8］逐漸成熟的條件下，基于SiPESC.FEMS、工程數據庫管理系統及插件技術設計開發出了結構拓撲優化設計模塊SiPESC.TOPO.目前，此模塊主要圍繞結構剛度設計功能進行開發，具有以下特點：

（1）給定結構剛度要求的最小化結構重量設計；

（2）給定材料用量約束下的結構最大化剛度設計；

（3）采用結構最大化剛度設計的廣義算法列式，可以考慮彈性力學的三類邊界條件；

（4）提供多種密度過濾策略以及靈敏度過濾來控制優化迭代的數值不穩定現象；

（5）可靈活選用準則法、數學規劃法（MMA、SLP、SQP）等優化算法；

（6）跨平臺，支持Linux、Windows等操作系統；

（7）組合結構優化，設計變量支持膜、板、殼、實體等單元，結構響應分析支持SiPESC.FEMS所具有的所有單元類型.

本文介紹SiPESC.TOPO的設計思路，并以結構最大剛度設計為例闡述SiPESC.TOPO的設計與實現方法.

1 SiPESC系統功能簡介

SiPESC.TOPO是基于SiPESC平臺開發的結構拓撲優化模塊，其開發過程延續了SiPESC系統“平臺／微核心＋插件”的設計思想，開發者借助開放接口將優化功能與現有分析模塊SiPESC.FEMS通過插件管理系統集成，同時依靠工程數據庫管理系統實現數據的統一管理.

如圖2所示的插件式體系結構是一種靈活的組件式結構，它將程序的功能打散，分布于不同插件中.插件作為獨立于程序系統的開發模塊，能夠動態地插入系統，并且可以被自由地加載、卸載或替換.結構拓撲優化模塊SiPESC.TOPO是具備多個應用插件的系統.

圖2 插件體系結構Fig.2 Architecture of plugin

SiPESC工程數據庫管理系統采用統一的數據管理接口，實現了大規模計算中的多類型數據、大數據塊（如總剛度陣）的管理.采用高效的數據存儲、動態擴展和檢索技術，實現了計算數據的高效訪問.采用索引的方式來實現對ID的快速檢索功能；同類型數據ID的唯一性保證了查詢算法的高效性.以結構拓撲優化為例，為消除網格依賴、棋盤格式等數值不穩定現象，優化過程中需要對靈敏度或者密度進行過濾，而目標單元的鄰域及鄰域內各個單元權重的計算和存儲都需要對系統數據庫進行操作，借助數據ID可方便準確地實現這些操作.

2 SiPESC.TOPO的設計思路

拓撲優化求解過程主要包括結構拓撲更新、結構響應分析、優化問題建立、優化問題求解以及優化過程異常處理5個要素，它們依據各自的算法理論獨立求解.SiPESC.TOPO的設計目標是實現各部分求解算法的動態選擇、替換（如靈敏度過濾與密度過濾等的動態選擇、最優準則法與各種數學規劃法的動態替換）.

2.1 結構拓撲優化設計流程

對于連續體結構的拓撲優化問題，采用有限元方法進行求解時，其基本流程如圖3所示.首先將結構用有限單元進行離散，施加荷載和位移邊界條件，得到結構模型數字化信息；其次，在模型中選取部分單元定義為優化問題的設計域；再次，對結構進行有限元分析，計算優化問題求解所需要的各種響應，并進行相應的靈敏度計算；將響應值以及靈敏度值代入優化算法程序來更新設計變量，以此實現結構拓撲的改變；最后對更新后的結構拓撲進行新一輪的分析優化直到收斂.

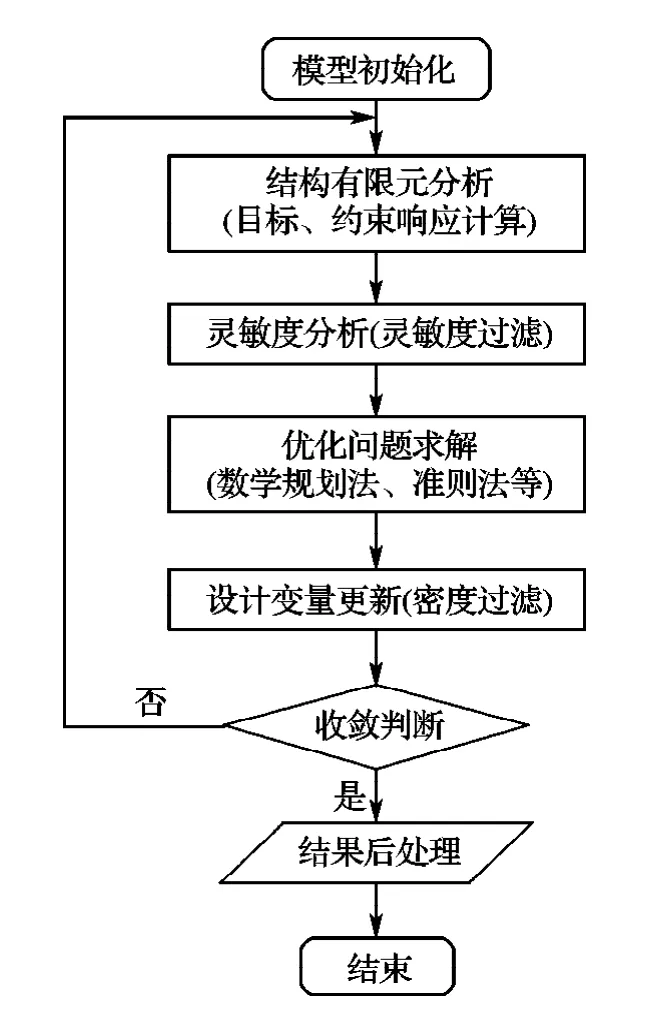
圖3 拓撲優化一般求解流程Fig.3 The general flow chart of topology optimization

2.2 SiPESC.TOPO需求分析

考慮到結構拓撲優化問題本身的復雜性和多樣性，在具體問題的求解過程中，可能用到不同的結構響應和優化算法，這就要求優化程序具有靈活性，能夠根據所解決的實際問題，方便地將不同功能進行動態組合.這就是開發SiPESC.TOPO的出發點和實現目標.

此外，在實際工作中，常用的CAE軟件已經無法滿足科研需求，特殊的問題需要更為專業的求解軟件，甚至需要研究人員自己開發求解程序.這就要求SiPESC.TOPO能夠方便地集成專業軟件的求解器或者是用戶開發的程序代碼，以此來提高科研工作效率.對于SiPESC.TOPO來說，插件管理平臺的可擴展性使用戶能夠根據自己的需求選擇相應的響應分析插件或編寫屬于自己問題的求解插件，動態地選擇或替換優化算法、過濾算法等.

3 SiPESC.TOPO程序實現

結構最大化剛度設計是拓撲優化中最一般的研究模型，也是商用軟件中最基本的功能.本章以此為例來介紹SiPESC.TOPO的具體實現方法.

在結構最大化剛度設計中，外力在結構變形過程中所做的功，即結構柔順性被用來作為目標函數.然而文獻［9］的研究工作指出，當結構在同時具有給定的外力和指定的非零位移情況下，即混合邊界條件下，傳統優化列式不再適用，需要采用他們提出的如下廣義優化列式：

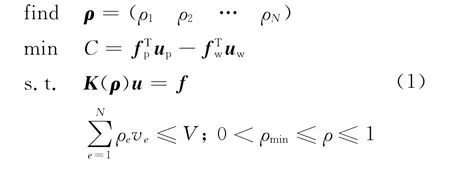
上述列式適用于所有彈性力學三類邊界條件下的結構最大化剛度設計.其中N表示設計域內的有限單元個數；ρ為設計變量向量，即單元人工密度向量；K為結構總體剛度矩陣，由單元剛度矩陣累加而成；V為給定的材料總量；fp和uw分別是已知的外力向量和指定非零位移向量；up和fw是相應的位移未知向量和反力未知向量，fw可借助有限元分析模塊SiPESC.FEMS中的org.sipesc.fems.MComputeKU擴展來求解.

在SiPESC.TOPO中，本文選用式（1）來建立優化模型.圖4給出了結構拓撲優化插件的主要結構，其包括的擴展有：（1）插值模型擴展；（2）優化算法擴展；（3）過濾函數擴展；（4）文件輸入輸出擴展；（5）結構響應計算擴展.其中（1）和（5）屬于工具擴展，暫不考慮其擴展性；針對具有多種可選算法的（2）、（3），本文采用設計模式中的工廠方法［10］，首先定義用戶可見的抽象類，然后在子類中重定義抽象操作即實現具體算法，最后利用工廠對象實現子類的動態調用.下面就上述主要擴展進行詳細說明.

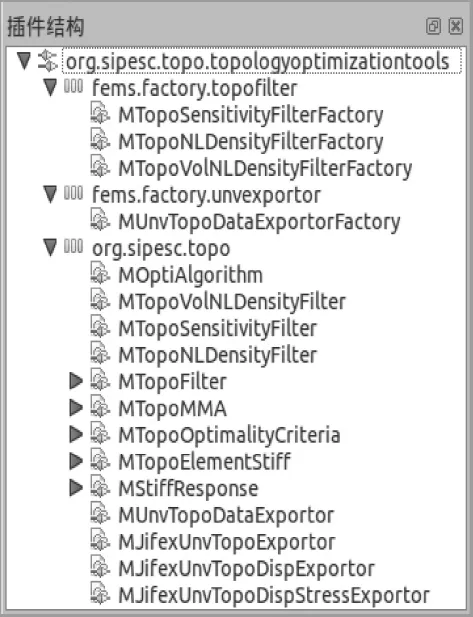
圖4 使用插件設計器創建的擴展Fig.4 The extension created by plugin designer

3.1 插值模型擴展

擴展名：org.sipesc.topo.MTopoElementStiff

此擴展的功能是通過引入合理拓撲變量插值模型，將原有的離散變量優化問題連續化以便于優化問題的求解.這里選用SIMP插值模型，它通過對中間密度材料的單元剛度進行懲罰使得連續變量優化問題趨近于原來的0－1優化問題.擴展主要接口如下：

（1）擴展初始化：bool initialize（var，…）；

（2）提取單元剛度矩陣：MMatrix getElementStiff（var，…）；

（3）修改單元剛度矩陣：bool updateElement－Stiff（var，…）.

3.2 優化算法擴展

擴展名：org.sipesc.topo.MOptiAlgorithm.

此擴展的功能是選取合適的優化算法對已經建立的優化模型進行求解.目前常用的優化算法主要有優化準則法和數學規劃算法，前者針對不同類型的優化問題需要推導不同的優化準則，一般用于單約束情況，但其求解速度較快；后者不但能夠用于單約束情況，而且能用于多目標多約束等復雜工程問題的求解建模，更為可靠.

考慮到優化準則法與數學規劃法的不同特點，SiPESC.TOPO中，數學規劃法作為通用算法，優化準則法作為定制算法使用.SiPESC平臺的可擴展性能使不同算法靈活添加、調用，用戶依據具體工程問題利用接口編程定制插件，即插即用.當用戶需要使用新的算法時，只需繼承此虛基類并重新實現下面的接口即可.擴展主要接口如下：

（1）擴展初始化：bool initialize（var，…）；

（2）優化問題求解：bool update（var，…）.

3.3 過濾函數擴展

擴展名：org.sipesc.topo.MTopoFilter.

此擴展的功能是利用過濾技術解決優化過程中的數值問題，例如，解決拓撲優化中的棋盤格式、網格依賴性及灰度單元等數值問題，相對于其他方法具有概念簡單、容易操作以及通用性強的優點.本擴展主要采用密度過濾類算法，實現了Xu等［11］提出的體積守恒型非線性密度過濾策略.此擴展主要接口如下：

（1）擴展初始化：bool initialize（var，…）；

（2）靈敏度更新：QMap〈int，double〉updateSensitivity（var，…）.

考慮到程序開發的長遠需要，工廠模式被用來設計此擴展.所設計的工廠對象根據過濾算法類型動態創建具體算法，實現算法的動態調用.例如，針對體積守恒的非線性密度過濾方法，調用代碼如下：

這里，MTopoVolNLDensityFilter為工廠對象，MTopoFilter為過濾算法的基類，所有的過濾算法均基于基類實現，按基類方法調用，保證了代碼統一性；系統擴展性由工廠機制完成，即上述代碼中的工廠名稱可動態替換.

3.4 結構響應計算擴展

擴展名：org.sipesc.topo.MStiffResponse.

此擴展是一個工具擴展，其作用是根據結構有限元分析結果來計算優化模型中的目標／約束函數值以及相關的靈敏度.對于基于廣義列式描述的結構最大化剛度設計問題，求解式（1）中所定義的目標函數時，需要分開計算指定位移uw處的反力fw，以及指定外力fp處的位移up，然而此目標函數對設計變量的靈敏度的計算仍需要求解單元應變能.其主要接口如下：

（1）單元應變能計算：double getElement－UTK0U（var，…）；

（2）單元體積計算：double getElement－Vol（var，…）；

（3）目標函數計算：double getGeneral－Stiff（var，…）.

對于目標函數的計算，當結構受到混合邊界條件作用時，調用SiPESC.FEMS中的擴展MComputeKU；當結構僅受指定外力或是指定位移作用時，目標函數自動退化為應變能的表達，此時調用單元應變能計算擴展更為簡單.

3.5 軟件研發模式

基于SiPESC平臺的關鍵技術是插件和數據庫.SiPESC.TOPO針對結構拓撲優化計算的需求，開發了相應的擴展模塊，利用已有的插件和數據庫系統完成了計算功能；構建了整體的優化求解流程，并針對可能的擴展需求，提出了基于工廠模式的解決方案.作為平臺類軟件的研發，開放性是核心目標；SiPESC.TOPO實現的框架和開放性機制，為將來的多人／多組織協同開發提供了機制和模式，也為功能動態擴展提供了保證.上述介紹的擴展，均可在后續應用中被二次開發模塊調用，也可以在需要擴展處實現動態替換／更新.

4 SiPESC.TOPO算例

4.1 二維懸臂梁拓撲優化設計

如圖5（a）所示的懸臂梁結構，長L＝2m，高H＝1m，左端根部固定，右端中點作用豎直向下的集中力P＝100.0N.材料的彈性模量E＝10.0 MPa，泊松比ν＝0.3，材料體分比為0.3，進行最大剛度設計.

采用四節點平面應力單元對結構進行離散，初始網格劃分100×50.采用體積守恒型非線性密度過濾，過濾半徑0.05m，優化求解采用MMA算法.優化后的最優拓撲如圖5（b）所示，最優設計拓撲構型清晰，傳力路徑合理；目標函數迭代歷史曲線如圖5（c）所示，目標光滑收斂.此經典算例驗證了SiPESC.TOPO拓撲優化功能的正確性.

圖5 二維懸臂梁算例Fig.5 2－D cantilever beam example

4.2 三維結構拓撲優化設計

如圖6（a）所示的正六面體初始設計域，l1＝0.90m，l2＝0.45m，模型底部4個角點固定，頂部表面受對稱的線荷載P＝10.0kN／m作用.材料的彈性模量E＝68.0GPa，泊松比ν＝0.3，材料體分比為0.25，進行最大剛度設計.

采用八節點正六面體單元對結構進行離散，初始網格30×30×30.同4.1一樣，仍然采用體積守恒型非線性密度過濾，過濾半徑0.05m，優化求解采用MMA算法.優化后的最優拓撲如圖6（b）所示，得到了清晰的結構拓撲；目標函數迭代歷史曲線如圖6（c）所示，曲線收斂光滑.此算例說明SiPESC.TOPO可用于求解三維結構拓撲優化問題.

圖6 三維結構優化算例Fig.6 3－D structure optimization example

4.3 混合邊界條件下結構拓撲優化設計

如圖7所示兩端固支梁，寬400mm，高100 mm，單位厚度，結構同時受到A點豎直向上的外力F＝1N和B點豎直向下的指定位移D＝10mm的作用.材料的彈性模量和泊松比分別為1.0MPa和0.3.材料體分比為0.3，進行最大剛度設計.

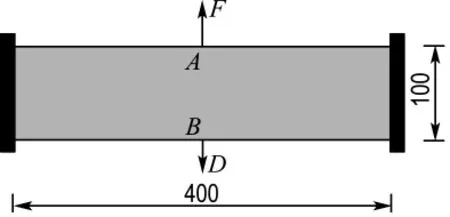
圖7 兩端固支梁模型Fig.7 The beam model clamped at both ends

采用四節點平面應力單元對結構進行網格離散，初始網格劃分200×50.同4.1一樣，仍然采用體積守恒型非線性密度過濾，過濾半徑4mm，優化求解采用 MMA算法.進一步，為了說明SiPESC.TOPO進行最大剛度設計時所采用的廣義優化列式的優越性，還分別采用了ANSYS、MSC.Nastran以及OptiStruct進行求解.其中OptiStruct對此種情況不予求解并給出錯誤警告，其他程序求解結果如圖8所示，可以看出，當結構邊界上同時作用有指定的外力和非零位移時，SiPESC.TOPO得到了清晰的拓撲構型，并且迭代過程穩定收斂.ANSYS和MSC.Nastran雖能以最小化柔順性為目標函數進行求解并也給出了材料分布，但是從目標函數迭代歷史曲線來看違反了最小化要求，不理想.

圖8 不同程序平臺的優化結果Fig.8 The optimal results under different program platforms

5 結論與展望

本文基于公共服務CAE軟件平臺SiPESC，探討了結構拓撲優化模塊SiPESC.TOPO的開發.該模塊在SIMP插值模型的基礎上實現了連續體結構拓撲優化，并能夠對優化過程中出現的棋盤格式、網格依賴性以及灰度單元等數值不穩定現象進行處理.更值得一提的是，該模塊的最大剛度設計功能依據最新提出的結構最大剛度設計的廣義優化列式，能夠適用于各類邊界條件的情況，這是其他商用程序所不具備的.

另外，SiPESC.TOPO結構拓撲優化模塊繼承了SiPESC平臺的優勢，具有較好的開放性，并且其內部插件的動態擴展，使得在此基礎上的二次開發靈活簡單.該拓撲優化模塊可對大規模的復雜結構進行拓撲優化設計，能夠將結構的建模、分析、優化、可視化等系列操作集成一身，并具備跨平臺優勢.因此SiPESC.TOPO適合于理論和算法研究；同時隨著SiPESC.FEMS功能提升，SiPESC.TOPO將具備解決大規模復雜工程問題拓撲優化的能力.

目前此模塊依然處于開發階段，在求解問題種類、優化效率、用戶界面操作性方面需要進一步拓展與完善，研究工作的目標是逐步構建結構拓撲優化領域面向科學研究與工程應用的開放計算平臺.

［1］Bends e M P，Sigmund O.Topology Optimization：Theory，Methods，and Applications ［M］.New York：Springer，2003.

［2］Bends e M P， Kikuchi N.Generating optimal topologies in structural design using a homogenization method ［J］.Computer Methods in Applied Mechanics and Engineering，1988，71（2）：197－224.

［3］Bends e M P.Optimal shape design as a material distribution problem ［J］.Structural Optimization，1989，1（4）：193－202.

［4］Xie Y M，Steven G P.A simple evolutionary procedure for structural optimization ［J］.Computers ＆Structures，1993，49（5）：885－896.

［5］Sethian J A，Wiegmann A.Structural boundary design via level set and immersed interface methods［J］.Journal of Computational Physics，2000，163（2）：489－528.

［6］Rozvany G I N.A critical review of established methods of structural topology optimization ［J］.Structural and Multidisciplinary Optimization，2009，37（3）：217－237.

［7］張洪武，陳飆松，李云鵬，等.面向集成化CAE軟件開發的SiPESC研發工作進展［J］.計算機輔助工程，2011，20（2）：39－49.ZHANG Hong－wu，CHEN Biao－song，LI Yunpeng，etal.Advancement of design and implementation of SiPESC for development of integrated CAE software systems ［J］.Computer Aided Engineering，2011，20 （2）：39－49.（in Chinese）

［8］張 盛，楊東生，尹 進，等.SiPESC.FEMS的單元計算模塊設計模式［J］.計算機輔助工程，2011，20（3）：49－54.ZHANG Sheng，YANG Dong－sheng，YIN Jin，etal.Design pattern of element computation module of SiPESC.FEMS ［J］.Computer Aided Engineering，2011，20（3）：49－54.（in Chinese）

［9］NIU Fei，XU Sheng－li，CHENG Geng－dong.A general formulation of structural topology optimization for maximizing structural stiffness［J］.Structural and Multidisciplinary Optimization，2011，43（4）：561－572.

［10］Gamma E，Helm R，Johnson R，etal.Design Patterns：Elements of Reusable Object－oriented Software ［M］.Boston： Addison－Wesley Professional，1994：116－117.

［11］XU Sheng－li，CAI Yuan－wu，CHENG Geng－dong.Volume preserving nonlinear density filter based on heaviside functions ［J］.Structural and Multidisciplinary Optimization，2010，41（4）：495－505.