三階m－點邊值問題的正解

張海娥

（唐山學(xué)院 基礎(chǔ)教學(xué)部，河北 唐山063000）

考慮三階m－點邊值問題，

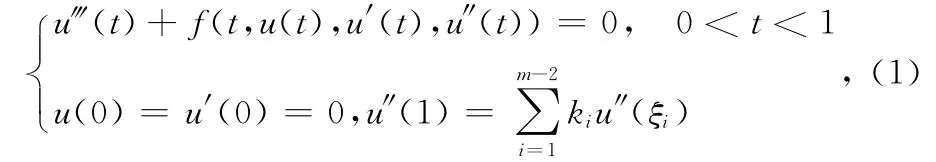
定理1 設(shè)E是Banach空間，KE是錐，Ω1和Ω2是E中有界開集，0∈Ω1，1Ω2，A：K∩（2＼Ω1）→K全連續(xù)，若A滿足：

（i）‖Au‖ ≤ ‖u‖，u∈K∩?Ω1，且 ‖Au‖≥‖u‖，u∈K∩?Ω2；

（ii）‖Au‖ ≥‖u‖，u∈K∩?Ω1，且‖Au‖≤‖u‖，u∈K∩?Ω2，

1 預(yù)備引理

引理1［5］對任意給定的y∈C［0，1］，邊值問題

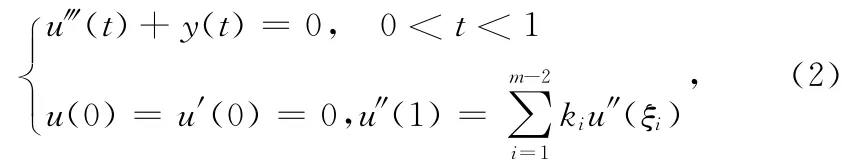
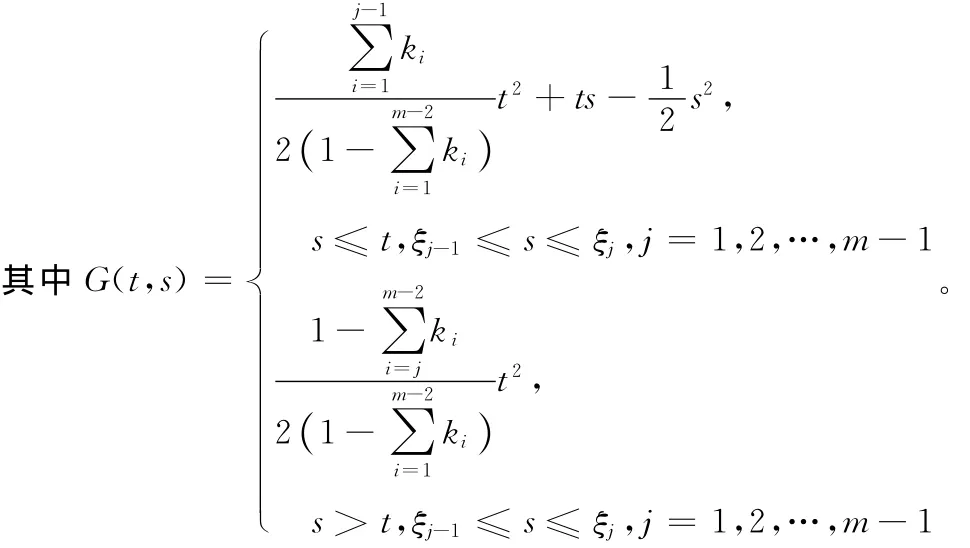
顯然，0≤G（t，s）≤G（1，s），t，s∈ ［0，1］。

引理2 令0＜θ＜1，對任意的y∈C＋［0，1］，BVP（2）的解u（t）非負(fù)且滿足

證明 由G（t，s）≥0和y（t）≥0，易得u（t）≥0。令u（t0）＝ ‖u‖，t0∈ ［θ，1］，下面證明

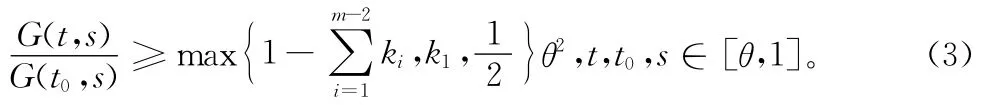
由于0≤s≤ξ1時，（3）式顯然成立，故只需證明ξj－1≤s≤ξj，j＝1，2，…，m－1的情況。

情形1：若0＜t，t0≤s，則

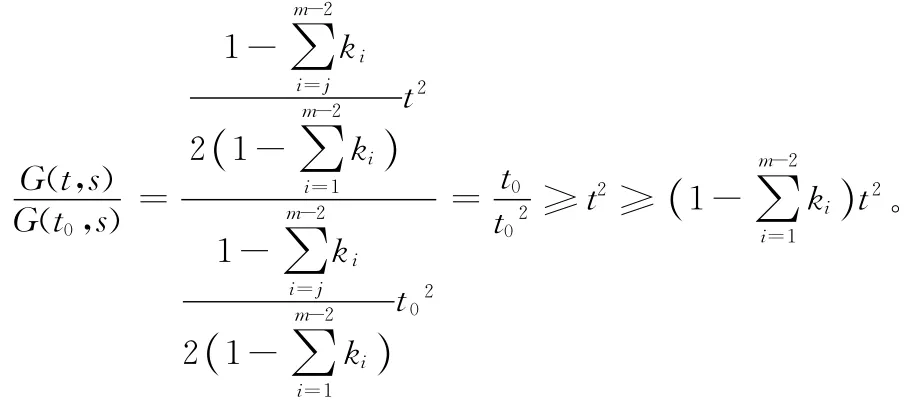
情形2：若0＜t≤s≤t0，則

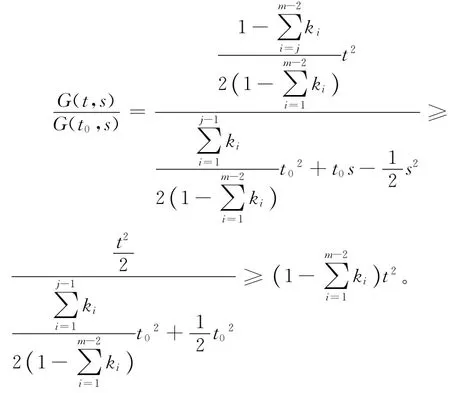
情形3：若0＜s≤t，t0，則

情形4：若0＜t0≤s≤t，則

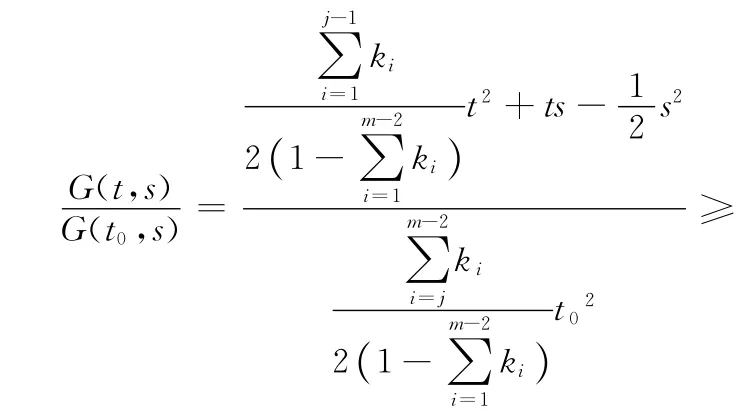
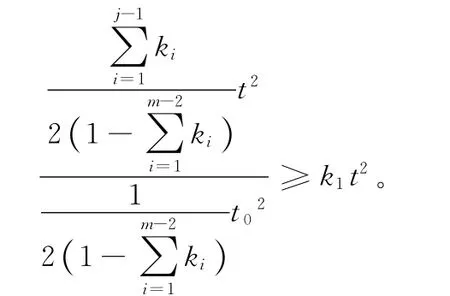
定義 K ＝ ｛u∈E，u（t）≥0，t∈ ［0，1］且≥δ‖u‖｝，易知K是E中的錐。對u∈K，定義算子T：K→K，Tu（t）＝G（t，s）f（s，u（s））ds，t∈ ［0，1］。由引理2可證得Tu（t）≥δ‖Tu‖。顯然，如果u是T 在K 中的不動點，則u是BVP（1）的解。

引理3 T：K→K是全連續(xù)的。

2 主要結(jié)論

為了方便起見，記：

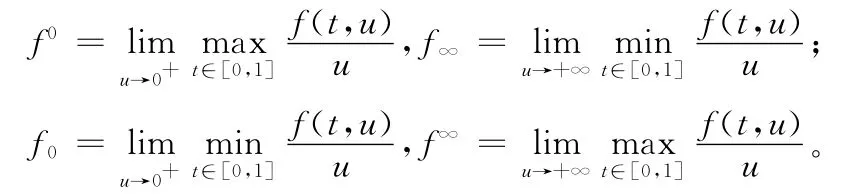
定理2 當(dāng)f0＝0，f∞＝∞（超線性）或f0＝∞，f∞＝0（次線性）時，則BVP（1）至少存在一個正解。

證明 首先，我們考慮超線性的情形。

由f0＝0，存在H1＞0使得當(dāng)0＜u≤H1時，f（t，u（t））≤M1u（t），其中 M1＞0滿足

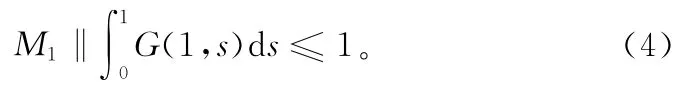
令Ω1＝｛u∈E：‖u‖＜H1｝，則對任意的u∈K∩Ω1，Au（t） ≤≤‖u‖，從而可得

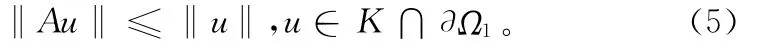
又由f∞＝ ∞，存在 H2′＞0，使得當(dāng)u≥ H2′ 時，f（t，u（t））≥ M2u（t），其中 M2＞0滿足

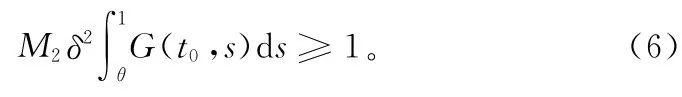
令H2＝max｛2 H1，H2／δ｝，Ω2＝ ｛u∈E：‖u‖ ＜H2｝，對任意得u∈K∩?Ω2，≥δ‖u‖ ≥H2′，故由式（3），可知Au（t）＝≥‖u‖，因此

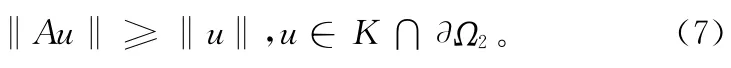
由定理1的前半部分可得A有不動點u＊∈K∩2＼Ω1，亦為BVP（1）的正解。

其次，我們考慮次線性情形。

又由f0＝∞，存在H1＞0，使得當(dāng)0＜u≤H1時，f（t，u（t））≥ M1′u（t），其中 M1′＞0滿足

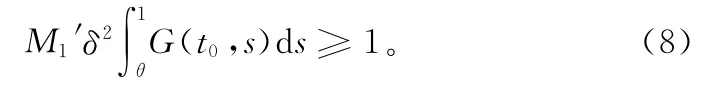
令Ω1＝｛u∈E：‖u‖＜H1｝，對任意的u∈K∩?Ω1故由式（8）可知Au（t）＝，s）f（s，u（s））ds ≥ ∫δ10 G（t0，s）f（s，u（s））ds≥δ2M1′‖u‖≥ ‖u‖，因此

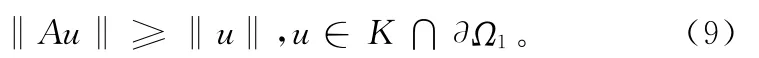
由f∞＝0，存在H2′＞0，使得當(dāng)u≥H2′時，f（t，u（t））≤M2′u（t），其中 M2′ ＞0滿足

分兩種情況考慮：

情況1：當(dāng)f有界時，即f（t，u（t））≤ N，u∈ ［0，＋∞），選取 H2＝ max ｛2 H1，NG（1，s）ds ｝。

令Ω2＝ ｛u∈E：‖u‖ ＜H2｝，則對任意的u∈K∩?Ω2，得

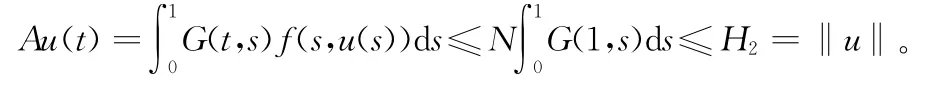
從而可得，‖Au‖ ≤ ‖u‖，u∈K∩?Ω2。 （11）

情況2：當(dāng)f無界時，選取 H2＞ max｛2 H1，H2′｝，使得f（t，u（t））≤f（H2），0＜u≤ H2。

對任意的u∈K∩?Ω2，由式（10）可得

由定理1的后半部分知A有不動點u＊＊∈K∩2＼Ω1，則BVP（1）至少有一個正解。

［1］ Anderson D R，Davis J M．Multiple solutions and eigenvalues for three－order right focal boundary value problems［J］．J．Math．Anal．Appl．，2002，267（1）：135－157．

［2］ Du Z J，Ge W G，Zhou M R．Singular perturbations for third－order nonlinear multi－point boundary value problem［J］．J．Differential Equations，2005，218（1）：69－90．

［3］ Yao Q L．The existence and multiplicity of positive solutions for a third－order three－point boundary value problem［J］．Acta Math．Appl．Sinica，2003，19（1）：117－122．

［4］ Zhang H E，Sun J P．A generalization of the Leggett－Williams fixed point theorem and its application［J］．J．Appl．Math．Comput，2012，39（1－2）：385－399．

［5］ Sun J P，Zhang H E．Exsitence of solutions to third－order m－point boundary value problems［J］．Electronic J．Differential Equations，2008，125：1－9．