基于Matlab GUI的麥克斯韋速率分布律的數(shù)字化教學研究*

◆湯劍鋒 歐陽錫城

1 引言

麥克斯韋速率分布律是分子動理論的重要結(jié)論之一，它是研究氣體分子碰撞、大量分子熱運動服從統(tǒng)計規(guī)律性等問題的重要理論依據(jù)，正確理解它對學習熱學非常有用。但是由于推導(dǎo)困難、公式復(fù)雜、曲線難畫，麥克斯韋速率分布律學習起來比較費力，成了熱學理論教學中的一個難點。

Matlab是由美國的MathWorks公司于20世紀80年代中期出品的一款商業(yè)數(shù)學軟件，由于優(yōu)秀的數(shù)值計算能力和卓越的數(shù)據(jù)可視能力，使其很快在數(shù)學軟件中大放異彩，與Mathematica、Maple、MathCAD一起并稱為四大數(shù)學軟件。通過Matlab的圖形用戶界面（Graphical User Interfaces，GUI）可以設(shè)計出一個界面友好、方便人機交互的圖形界面程序。在物理教學中，適當利用Matlab GUI建立直觀的物理圖像，有助于學生更好地理解物理概念，提高學習興趣，調(diào)動學習積極性[1-4]。本文利用Matlab GUI對麥克斯韋速率分布律的教學進行研究。

2 麥克斯韋速率分布律的主要內(nèi)容[5]

一定量理想氣體處于平衡態(tài)，設(shè)共有N個分子，速率分布在v→v+dv區(qū)間內(nèi)的分子數(shù)為dN，則為在此區(qū)間內(nèi)的分子數(shù)比率。實驗表明，與v的一定函數(shù)f(v)成正比，與v附近取的區(qū)間dv大小成正比，即：

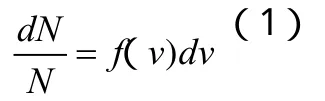
（1）式中的f(v)稱為速率分布函數(shù)。1859年，麥克斯韋導(dǎo)出了它的表達式：

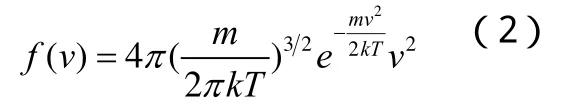
（2）式中的m是每個分子的質(zhì)量，T是氣體的熱力學溫度，k為波爾茲曼常數(shù)。

與f(v)取極大值對應(yīng)的速率叫做最概然速率，用vp表示，其表達式為：

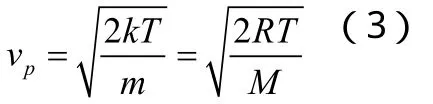
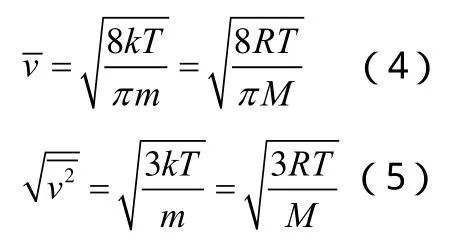
3 Matlab GUI 在麥克斯韋速率分布律教學中的應(yīng)用

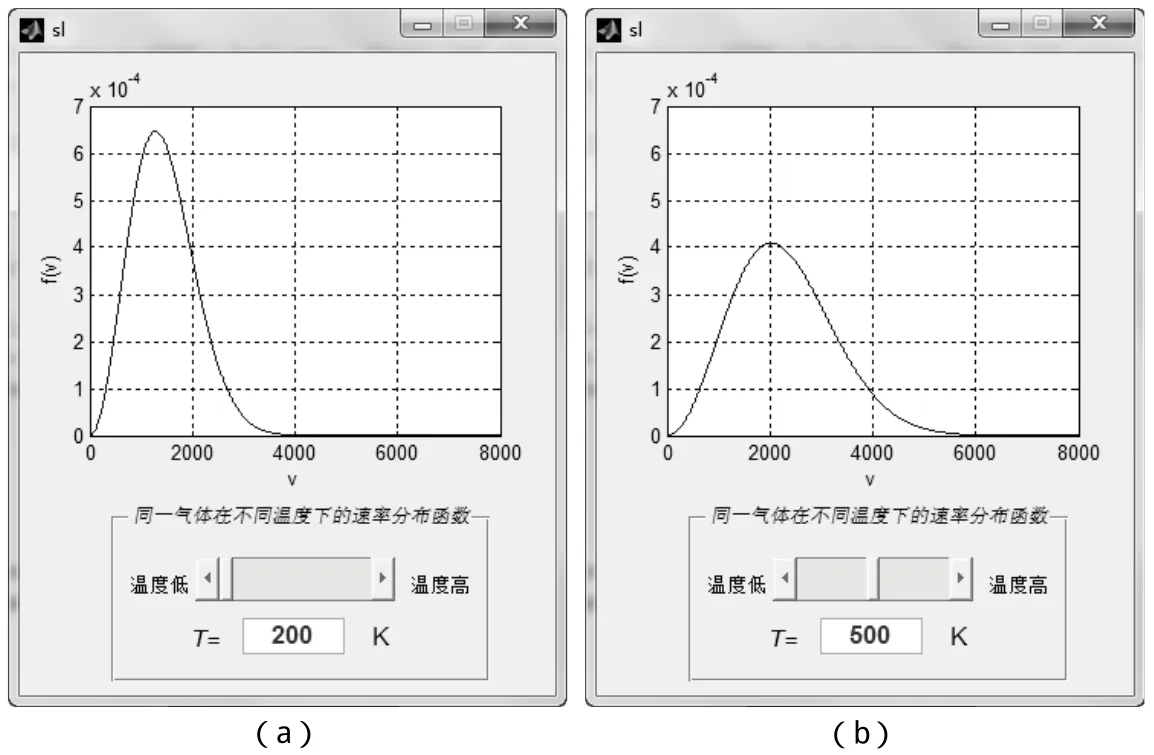
圖1 同一氣體在不同溫度下的速率分布曲線對比

同一氣體在不同溫度下的速率分布曲線對比 圖1中的（a）和（b）分別為同一種氣體在200 K和500 K時的速率分布曲線。可以明顯看出：（b）圖比（a）圖平坦，且vp值較小。這是因為對于同一種氣體，溫度越高，分子運動越劇烈，分布曲線中的最概然速率vp越大，但歸一化條件要求曲線下總面積不變，因此分布曲線變平坦，高度降低。

當用鼠標拖動程序中的滑動條或點擊滑動條兩側(cè)的三角形箭頭時，溫度可以在200～800 K的范圍內(nèi)變化，上方的圖形也會隨之發(fā)生變化，能夠非常形象地觀察同一氣體在不同溫度下的速率分布曲線變化規(guī)律。

滑動條的回調(diào)函數(shù)代碼如下：

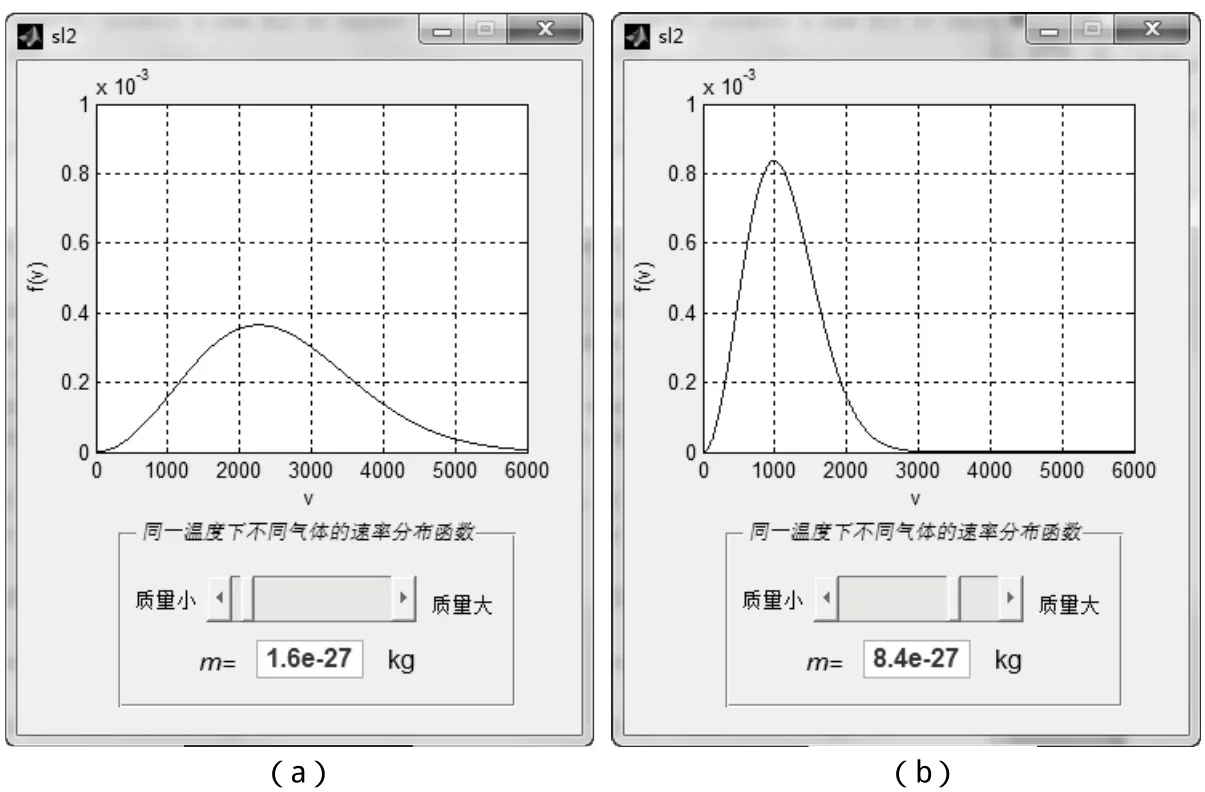
圖2 同一溫度下不同氣體的速率分布曲線對比

同一溫度下不同氣體的速率分布曲線對比 圖2是同一溫度下不同氣體的速率分布曲線對比圖，其中的（a）圖分子質(zhì)量為1.6×10-27kg，（b）圖分子質(zhì)量為8.4×10-27kg。可見，在同一溫度下，隨著氣體分子質(zhì)量的增加，vp值會減小，分布曲線則變陡峭，以保證曲線下總面積不變。

類似的，程序中的分子質(zhì)量可以在200～800 K的范圍內(nèi)變化，可以形象地觀察同一溫度下不同氣體的速率分布曲線變化規(guī)律。

三種統(tǒng)計速率的計算 3種統(tǒng)計速率含義各不相同：最概然速率反映了速率分布的基本特征，平均速率反映了分子平動的平均效果，方均根速率則與分子平均平動動能有關(guān)。從（3）～（5）式可以看出，任何氣體在同一溫度下，。

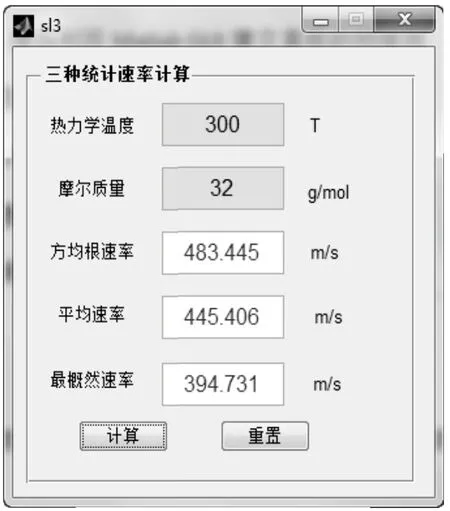
圖3 三種統(tǒng)計速率的計算

圖3是用Matlab GUI設(shè)計的計算3種統(tǒng)計速率的程序。在熱力學溫度后面的矩形框中輸入溫度，在摩爾質(zhì)量后輸入氣體的摩爾質(zhì)量，點擊“計算”按鈕就可以立即計算出3種速率的大小，清楚地看到它們的大小關(guān)系；點擊“重置”按鈕，可以把所有的矩形框中的數(shù)據(jù)清空，方便計算下一組數(shù)據(jù)。

4 結(jié)語

麥克斯韋速率分布律及由此得到的分布曲線和3種統(tǒng)計速率，為人類認識微觀的分子運動提供了許多信息，在物理學中占有非常重要的地位。運用Matlab GUI軟件將高度抽象概括的麥克斯韋速率分布律與非常形象直觀的物理圖像有機結(jié)合在一起，充分激發(fā)了學生的學習興趣，達到了提高教學質(zhì)量、優(yōu)化教學效果的目的。

[1]王向賢,朱浩瑞,邵瑞,等.基于MATLAB的麥克斯韋速率分布函數(shù)的數(shù)字化教學[J].宜春學院學報,2011(4):17-19.

[2]孫燕,姜占才.麥克斯韋速度分布律的計算機輔助教學[J].計算機與現(xiàn)代化,2008(6):127-128.

[3]葉劍鋒.利用MATLAB圖形技術(shù)實現(xiàn)麥克斯韋速度分布律教學可視化[J].黃山學院學報,2012(5):105-108.

[4]魏中華,姜占才,宋云飛.Matlab在麥克斯韋速率研究中的應(yīng)用[J].科技信息,2013(2):148-149.

[5]程守洙.普通物理學1[M].5版.北京:高等教育出版社,1998.