利用信息技術開展數學探究活動案例簡析

◆吳帥榮

以“探究最大視覺和最佳觀測位置”為例，介紹學生如何用信息技術開展數學探究活動。學生在教師的引導下，根據操作提示，以小組為單位，動手操作計算機，親身參與到知識探究過程。學生通過自身的積極思考與同伴的合作交流等活動，達到掌握新知識、培養良好的數學思維品質，培養學生創新思維和應用數學知識的意識。

1 問題的提出

隨著當今社會知識信息激增和“減負提素”工作的深入開展，傳統教育面臨巨大的挑戰，教學手段和教學方法的更新勢在必行。數學作為一門中學主要學科，傳統的教學手段黑板加粉筆，偶爾加一些模型，同時由于數學本身不具有某些學科形象、生動、具體等特點，學生學起來難免有些枯燥無味，這直接影響學生學習數學的積極性。信息技術不僅有強大的計算功能，還有良好的交互界面，這無疑給數學教學改革帶來一片生機。教師應利用信息技術開展數學探究活動，減少解決問題過程中的機械的、重復性的勞動，提高數據的表達效率，使學生把更多的時間用于理解數學本質、探究數學規律上，從而提高數學教學效率，發展學生思維能力。

2 數學探究與信息技術概述

新課標要求“學生的數學學習活動不應只限于接受、記憶、模仿和練習，還應該倡導自主探究、動手實踐、合作交流、閱讀自學等學習數學方式”。因此，在數學教學中應該積極開展各種不同形式的數學探究活動，讓學生體驗數學發現和創造的歷程，發展他們的創新意識。

“數學探究”即數學探究性課題學習，是指學生圍繞某個數學問題，自主探究、學習的過程。這個過程包括：觀察分析數學事實，提出有意義的數學問題，猜測、探求適當的數學結論或規律，給出解釋或證明[1]。可見，數學探究是新課程下有效開展高中數學教學的一種重要的學習方式。與此同時，現代計算機技術計算能力以及圖形表達能力不斷提高，數學軟件如幾何畫板、MATLAB等軟件不斷完善。信息技術對數學課程、數學教學、數學學習等方面產生深刻的影響。它一方面突破數學教學中的重點和難點，進而優化教學形式、數學教學內容、學習過程；另一方面，在進行數學探究活動過程中，更能充分體現學生在學習中的主體地位。利用信息技術開展數學探究性活動主要包括創設問題情境、展示數量關系、探究發現規律、科學檢驗等環節。合理使用信息技術有助于呈現以往數學教學中難以呈現的課程內容，有助于學生對數學邏輯關系的直觀感受。它在數學教學中的應用對數學教學方式產生積極而深遠的影響。

3 “探究最大視覺和最佳觀測位置”的教學過程

以下是筆者最近組織學生，以小組合作學習的方式，使用幾何畫板軟件，進行數學探究性課題活動的教學課例，以供大家進行討論，歡迎提出寶貴建議。

3.1 提出問題，激發學習興趣

1471年，德國數學家J.米勒提出如下問題：

一尊英雄塑像，高H米，塑像底座高p米，一人從遠處注視塑像朝它走去，此人眼離地面h米，問此人走到哪一點觀看塑像時覺得塑像最大（即視角最大）？不妨設H=10米，p=13米，h=1.8米。

設計意圖：選擇有趣的問題背景，在學生“最近發展區”里提出有意義的數學問題，激發學生學習動機，提高學習興趣。

3.2 動手操作，創設探究情景

師：請同學們按下列提示的操作步驟，以小組為單位，合力完成下列探究活動。

操作提示：

1）啟動幾何畫板5.03；

2）點擊【繪圖】|【定義坐標系】菜單，建立平面直角坐標系，可以把x軸看作地平線；

3）新建參數H、p、h，并設置初始值為10、13、5；

4）計算H+p，并分別繪制點A(H+p,0)，B(p,0)，則線段BA就是塑像的位置，OB就是塑像的座高；

5）在x軸上任意取一點C，測量點C橫坐標xC，并繪制點D(xC,h)，則點D就是人眼的位置；

6）連接線段CD、AD、BD，為了方便觀察，可以把線段AD、BD改為虛線，于是∠ADB可以看作人的視角（如圖1所示）。

設計意圖：學生在幾何畫板上根據操作步驟，模擬實際的觀察情況，為學生進行科學的探究活動做好準備。

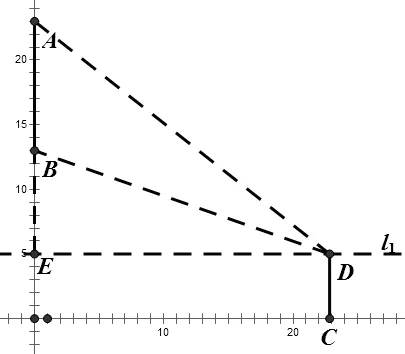
圖1

3.3 觀察現象，探究數量關系

探究活動一：利用幾何畫板的動態演示功能，初次感受最大視角的位置

1）測量∠ADB的大小，并繪制點P(xC,∠ADB)，并選擇點P，同時，按“Ctrl+T”組合鍵，追蹤點P移動軌跡。請你拖動點C，看∠ADB的大小有何變化？

2）依次選擇點C、點P，點擊菜單【構造】|【軌跡】，觀察點P的軌跡是什么？有何變化？

3）請你拖動點C的位置，結合∠ADB大小變化，探究視角最大時，點C所在位置。

設計意圖：學生通過動手操作，親身感受觀察視角∠ADB隨OC的距離變化而變化（如圖2所示），得出最佳觀察點的大概位置

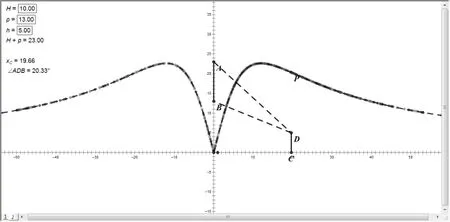
圖2

3.4 深入探究，發現數學規律

探究活動二：探究最近觀察點的位置

師：請同學們認真思考，相互交流，看看最佳觀察位置在哪里？

有些學生動手操作，有些學生開始交流

生：過點D作直線l1，它與y軸相交于點E；作過點A、點B與直線l1相切的圓，其切點Q就是人觀察AB的視角最大的地方（如圖3所示）。

師：你能說說你的理由嗎？

生：如圖4所示，人眼在水平線l1上，除點Q外，直線l1上任意一點都在圓外，如果眼在Q點的右側D點，不妨BD與圓相交于點F，連接AQ、BQ、AF，則∠AFB=∠AQB，而∠AFB是△AFD的外角，于是∠AFB＞∠ADB，所以∠AQB＞∠ADB。若眼在點Q的左側，同理可證視角小于∠AQB。所以∠AQB是最大視角，Q點是最優觀察點。

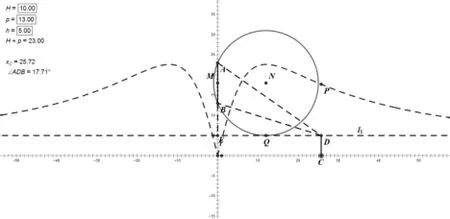
圖3

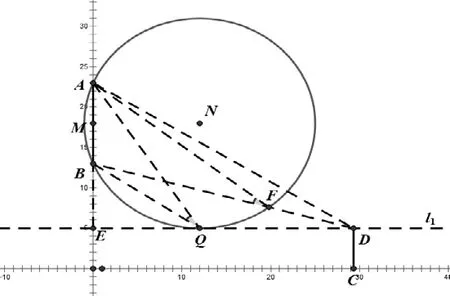
圖4

探究活動三：求出最佳觀察點的位置大小

師：回答得非常棒，既然點Q是最優觀察點，也就是說EQ就是距離觀察點觀察的最優距離，請問如何求出EQ的長度呢？

生：我有一種方法：

∵l1是圓N的切線

∴∠BQE=∠QAE

∴Rt△BEQ∽Rt△QEA

∴EQ2=BE·AE

∵AE=H+p-h，BE=p-h

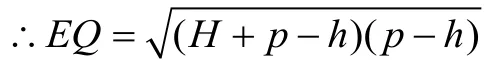
師：還有其他方法嗎？

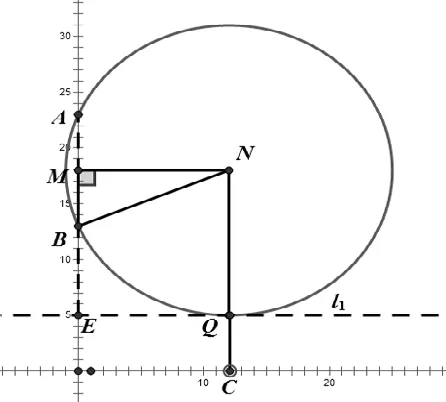
圖5

生：構造直角三角形（如圖5所示），利用勾股定理：

作AB的中點M，連接BN、MN，則△BNM為直角三角形。由條件得：

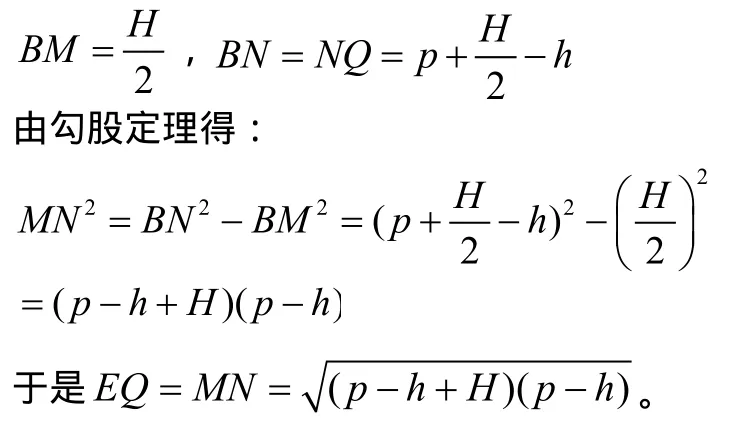
3.5 科學驗證，完美解答

師：利用上式，當H=10米，p=13米，h=5米時，大家計算最佳觀察點在哪里？

學生進行計算，很快就得出：

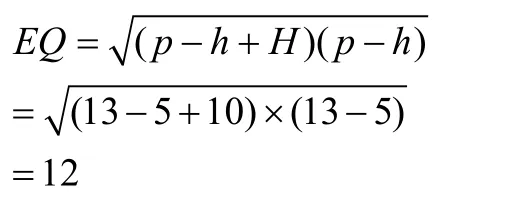
所以，最佳觀察點在距離底座12米處。

師：我們再一次利用計算機進行驗算，看看這個關鍵點是不是落在12米處。

生：通過移動點C，并跟蹤∠ADB的大小（如圖6所示），在距離原點12處，∠ADB達到最大值，所以最佳觀察點在距離底座12米處。

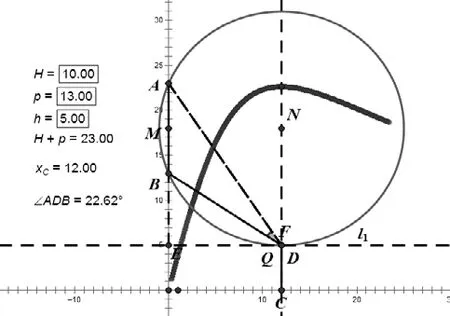
圖6

3.6 暢談體會，共同提高

各組選一名代表談談上這節課的體會，教師小結本課，提出希望。

4 幾點體會

4.1 合理設問、巧選課題

維果斯基的“最近發展區理論”，認為學生的發展有兩種水平：一種是學生的現有水平，另一種是學生潛在的發展水平。兩者之間的差距就是“最近發展區”。教師要通過教學指導學生的思維實現從現有的發展水平到潛在發展水平過渡，以完成發展過程[2]。因此，教師必須了解和把握學生對某個知識點的現有發展水平，然后把學生的最近發展區劃分為幾個發展層次，最后設計引導學生實現思維最近發展區“思維躍遷”的教學策略。所以恰當選擇合適的探究課題，就成為提高學生“思維躍遷”的關鍵。課題的選擇一般來說具有幾個特點：要有助于學生對數學的理解，有助于學生體驗數學研究過程，有助于學生形成發現問題、探究問題的意識，有助于鼓勵學生發揮自己的想象力和創造性。課題應具有一定的開放性，課題的預備知識最好不超過學生現有的知識范圍。

4.2 處理“主導”與“主體”的關系

在開展數學探究活動的過程中，要充分發揮教師的主導作用和學生的主體作用。課堂的教學活動不應都是教師的講授，而更多地體現學生的自學、討論、調查、探索、解決問題等環節。教師的主導作用體現在創設好的問題環境，激發學生自主地探究解決問題的積極性和創造性上；學生的主體作用體現在對問題的探索發現解決的深度和方式盡量由學生自主控制和完成。實現以教為主到以學為主的重心轉移。

4.3 恰當使用信息技術，充分利用信息技術的優勢

現代信息技術的廣泛應用正對數學課程的內容、數學教學、數學學習等方面產生深遠的影響。它在教學中的優勢主要體現在快捷的計算功能、豐富的圖象呈現、大量數據的處理能力，以及提供交互式的學習和研究環境等方面。因此，教師在教學中，一方面應重視現代信息技術與教材的有機結合，充分利用現代信息技術的優勢，幫助學生更好地認識和理解數學，增強學生對數學學習的興趣，提高教學質量[3]；另一方面，特別要注意信息技術手段的作用是“輔助”，必須擺正位置，尤其警惕不能讓多媒體教學手段喧賓奪主。評價一節課的好壞，并不是看教育手段使用的多少，而要看是否開發了學生的智力，挖掘了學生的潛力，培養了學生的能力[4]。

[1]數學課程標準研制組.《普通高中數學課程標準（實驗）》解讀[M].南京:江蘇教育出版社,2004.

[2]周春荔,張燕勤,等.數學創新意識培養與智力開發[M].北京:首都師范大學出版社,2000.

[3]曹才翰,章建躍.中學數學教學概論[M].2版.北京:北京師范大學出版社,2008.

[4]邱學華,張良.嘗試教學策略[M].北京:北京師范大學出版社,2010.