溫度影響下炭纖維/環氧樹脂復合材料性能預示①

樊 鈺，葉定友，，陳汝訓

(1.第二炮兵工程大學，西安710025;2.中國航天科技集團公司四院，西安 710025)

0 引言

航天技術的發展對材料在溫度影響下的力學性能提出了很高要求。在某些情況下，研究材料的耐溫性能，正確地評價材料，使其能滿足服役要求，成為航天技術發展和材料科學研究的重要任務。

目前，炭纖維/環氧樹脂復合材料以其優異的熱力學性能，成為現代固體火箭發動機殼體的首選材料。國內外學者對復合材料在高低溫環境下的細觀和宏觀力學性能開展了系統的實驗研究［1－4］，實驗結果為建立典型微結構特征和宏觀力學性能的定量關系提供了驗證數據。但炭纖維/環氧樹脂復合材料的內部微觀結構非常復雜，有限的實驗數據還難以建立起微結構特征和材料性能的全面關系。同時，通過溫度力學實驗獲得復合材料在不同溫度下的各種力學性能，需耗費大量的時間以及人力物力，而且只能獲得幾個溫度點下的性能，不能連續測試溫度，無法得到完整的材料力學性能隨溫度變化規律。自20世紀80年代以來，國內外對炭纖維/環氧樹脂復合材料在溫度影響下的性能預測研究做了一定的工作［5－9］，但多數僅側重于某個方面的力學參數，缺乏系統性和普適性，尤其是針對固體火箭發動機殼體所用的炭纖維/環氧樹脂復合材料，更沒有在其高低溫寬溫度范圍內進行過系統、完整的力學性能預示。

本文結合熱彈性力學本構關系理論，利用混合定律和Tsai－Hahn準則，建立起基于溫度變化的炭纖維/環氧樹脂復合材料性能預示模型。梳理并分析寬溫度范圍內復合材料強度、模量與溫度變化的關系，預示該材料的單向力學性能隨溫度的變化規律，并與實驗結果相結合。該預示方法不僅可合理地揭示炭纖維/環氧樹脂復合材料復雜的溫度變化機理，還可用于評估固體火箭發動機復合材料殼體承受各類載荷的力學行為，極大地減小實驗帶來的成本及周期問題。

1 理論模型

1.1 理論預示模型的建立

通過對炭纖維/環氧樹脂復合材料在溫度影響下的力學性能試驗，可發現材料力學性能強度及模量均是隨溫度變化的變量。通過對文獻分析，發現對于樹脂及其復合材料的單向力學性能隨溫度變化的規律，可近似地用下式表達:

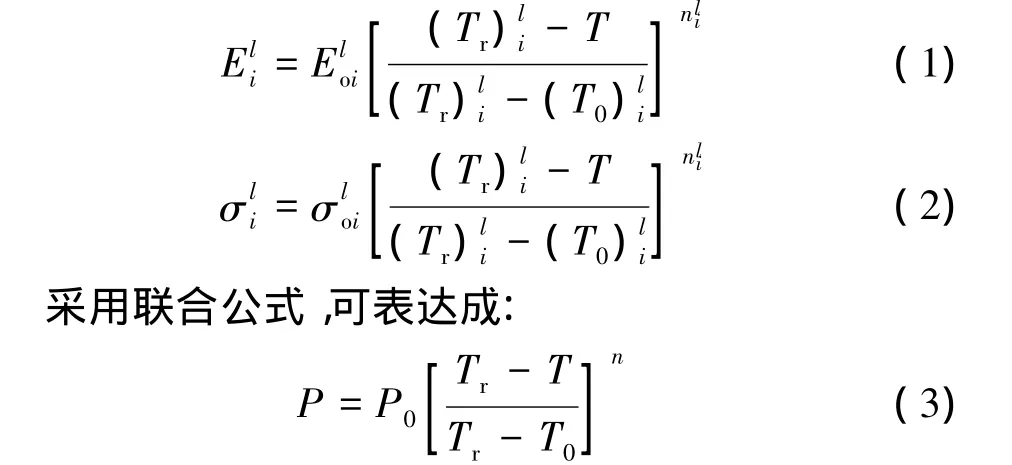
式中 P為材料在某一溫度T下的力學性能，如強度、模量等;P0為室溫下材料的性能;Tr為參考溫度，即材料性能變化可忽略的溫度;n為常數;T0和T分別為常溫和實際溫度。

P0、Tr和n是與溫度無關的常數。Tr和n可用最小二乘法求得，且對于固定體系的復合材料是一個常數。因此，若已知Tr和n，便可知該復合材料性能隨溫度變化的情況。Tr和n曲線可較好地反映樹脂的高溫性能變化規律，該公式不但適用于樹脂體系，也可用于復合材料體系。

綜上所述，當已知某類型復合材料的3～4個溫度點，就可應用式(3)模型很好地預測材料強度和模量隨溫度變化的規律。在基體樹脂和纖維材料的溫度力學性能已知的情況下，可利用“混合定律”和“Tsai－Hahn準則”，預測復合材料力學性能隨溫度變化的規律。

1.2 對理論模型中常數n的討論

當溫度升高時，即T＞T0時，整個溫度變化模型=為小于 1的數。分析可知，當 n0時，;0＜n＜ 說明材料性能隨溫度沒有變化 當1，且隨著n的增大，材料性能隨溫度的變化敏感度減小;當n=1時，材料性能隨溫度呈線性變化;當n＞1，且n越來越大時，溫度對于材料的影響越來越小，可不作為考慮的范圍。同時，由實驗可知，不論是樹脂還是復合材料，隨著溫度的升高，材料性能均呈現下降趨勢。因此，n值不可能出現負數。由以上分析可知，在溫度上升的情況下，理論模型式(3)中，n的取值范圍是0～1。

當溫度降低時，即T＜T0時，整個溫度變化模型=為大于1的數。同樣分析可知，當n0時，材料性能隨溫度沒有變化;當－1＜n＜0，且隨著n的減小，材料性能隨溫度的變化減小;當0＜n＜1，且隨著n的增大，材料性能隨溫度的變化增加;當n=1時，材料性能呈增加趨勢，且隨溫度呈線性變化;當n＞1且n越來越大時，溫度對于材料的影響越來越大。由低溫實驗可知，不論是樹脂還是復合材料，隨著溫度的降低，材料性能呈現上升、下降及保持不變3種趨勢。因此，n值可能呈現正負數形式。由以上分析可知，在溫度下降的情況下，理論模型式(3)中，n的取值范圍是－1～1。

1.3 對理論模型中材料性能保持率的討論

將理論模型公式(3)變形得

其中，P/P0是材料性能在某溫度T下的保留率，大多數評價則依據性能保留率50%～70%以上的溫度作為使用溫度。因此，可把從公式中求出性能保留率符合要求的使用溫度作為耐溫指標。對同一復合材料的不同性能及不同復合材料的同一性能，可進行縱向和橫向比較，討論理論模型公式中的Tr和n:

(1)高溫下，固定n，則Tr越大，性能保留率越大，說明材料的耐熱性好。如對縱向拉伸模量、強度，Tr趨于無窮大，這性能基本不隨溫度而改變。

(2)低溫下，固定n為正值，則Tr越大，性能保留率越低，耐低溫性能差;固定n為負值，則Tr越大，性能保留率越高，耐低溫性能好。如Tr趨于無窮大，這性能基本不隨溫度而改變。

(3)高溫下，固定Tr，則n越小，性能保留率越大，說明材料的耐熱性好。

(4)低溫下，固定Tr，n不論為正值還是負值，隨著n值的增大，材料性能保留率越高，即耐低溫性能越好。如n=0，則認為該材料性能不隨溫度而改變;如n=1，則認為該材料的性能保留率與溫度呈線性變化。

(5)若Tr和n均不固定，則往往很難比較。這時用程序及圖形軟件把曲線進行疊加，整個使用溫度范圍內，性能變化的情況便會一目了然。

2 實驗內容

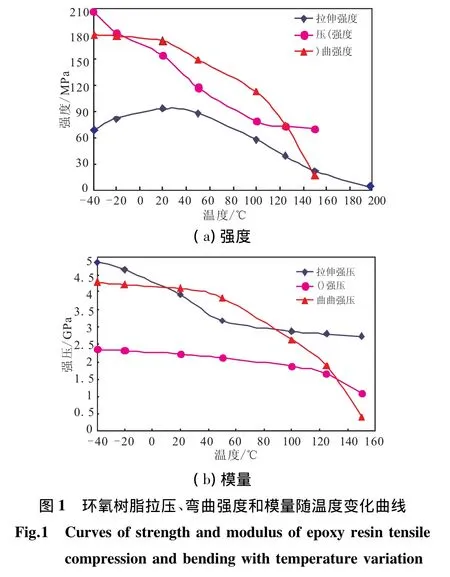
根據固體火箭發動機的研制發展需求，對炭纖維/環氧樹脂復合材料力學性能進行了系統的溫度實驗研究。由于高速飛行導彈在研制、生產、運輸、貯存過程中可能遇到各種氣候環境因素，同時在飛行過程中，彈體承受氣動加熱帶來的高溫、沖刷影響，而發動機與外熱防護材料之間的背壁溫度可能達到幾百攝氏度，發動機殼體必須進行外熱防護。基于以上因素，確定影響發動機殼體的溫度范圍，即低溫－40℃至高溫200℃。按照試驗相關標準，在此基礎上開展溫度影響下樹脂基體材料、復合材料層合板的力學性能實驗，見圖1和圖2。

3 分析與討論

3.1 環氧樹脂材料擬合數據及分析

根據前述的理論模型公式，由試驗的有限點可得到從低溫到高溫范圍內連續溫度的材料性能曲線，若要求性能達到某一值時，可用此公式求出相應的使用溫度;反之，給出使用溫度，也可求出此時所能達到的性能保留指標。

首先，對環氧樹脂材料進行曲線擬合，采用最小二乘法原理自編程序得到Tr和n，表1是環氧樹脂在高溫和低溫下的擬合參數。從表1可看出，所擬合出的Tr和n滿足1.2節中的討論結果。

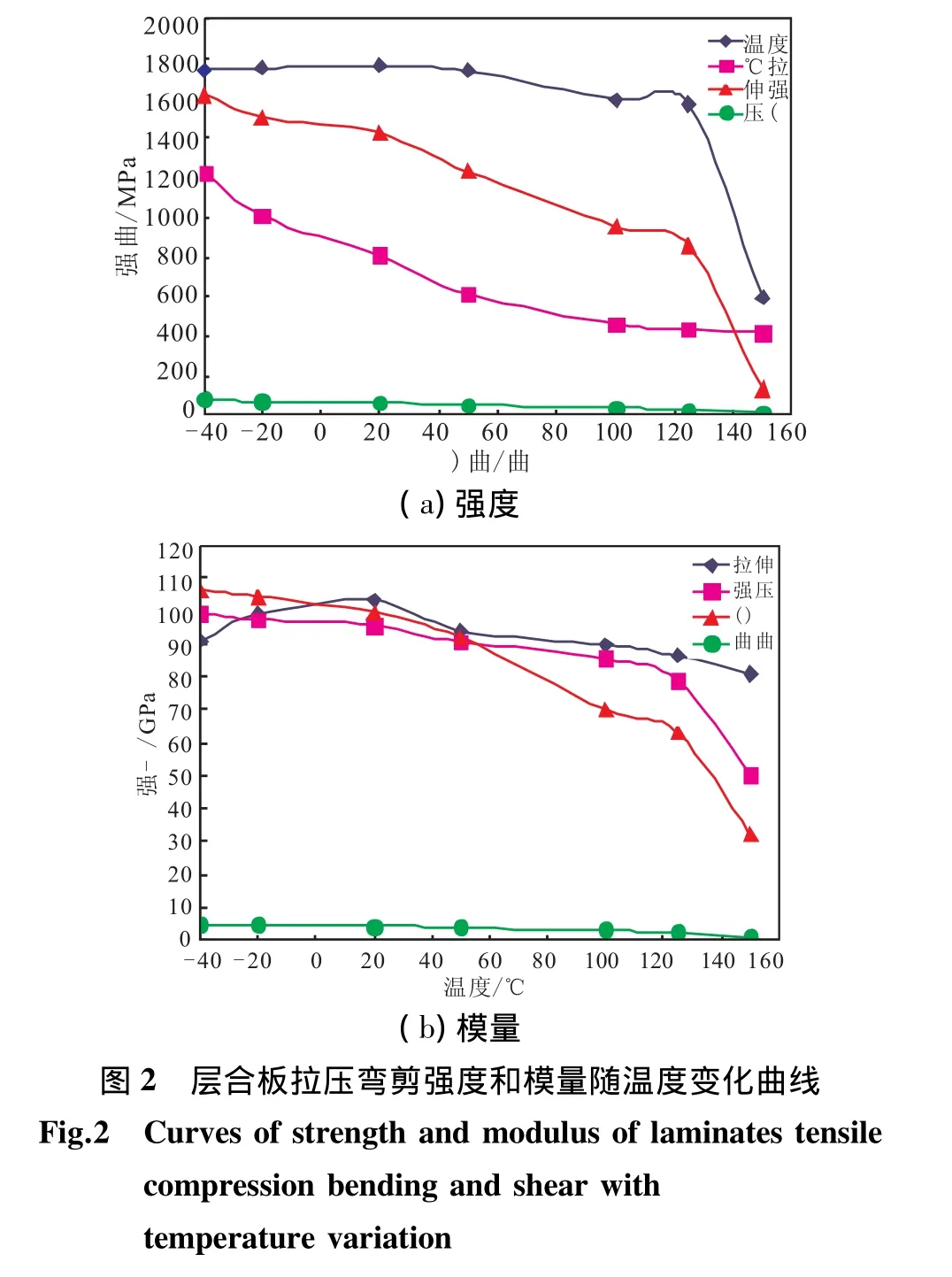
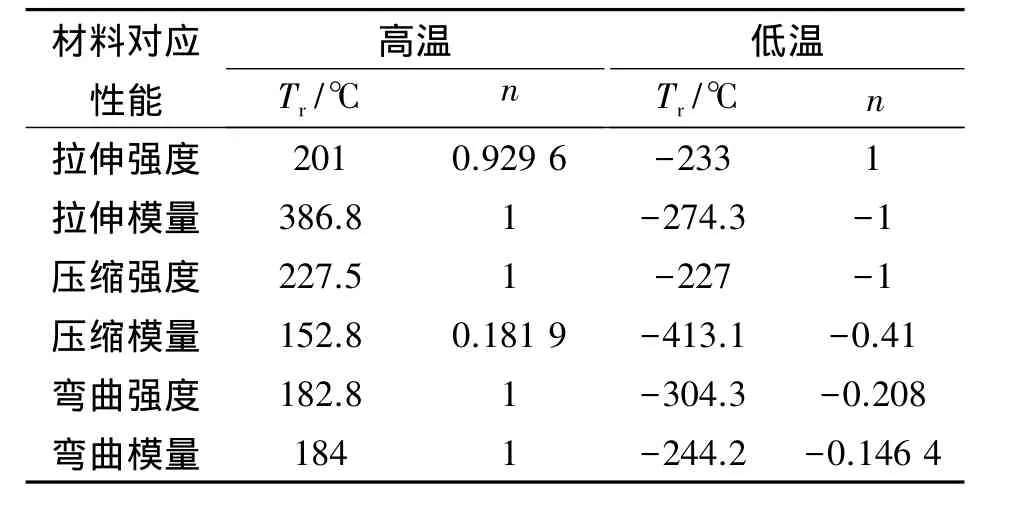
表1 環氧樹脂材料Tr和n擬合參數Table 1 Fitting parameters of Trand n of epoxy resin

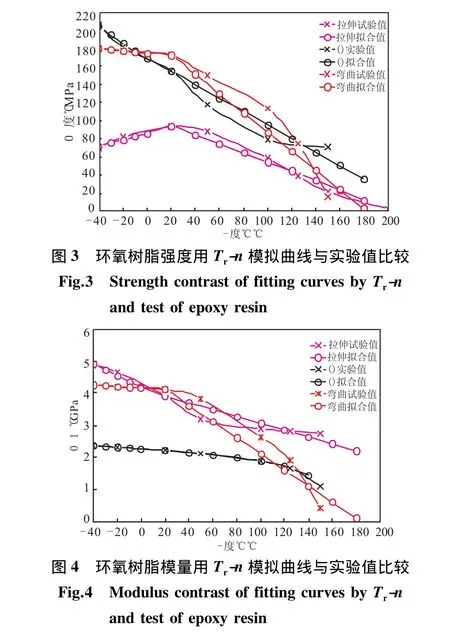
圖3和圖4分別是環氧樹脂材料在－40～200℃之間，拉伸、壓縮、彎曲強度和模量用Tr－n模擬出的數據與實際試驗值比較結果。從對比圖可看出，用所建立的數學模型，通過最小二乘法計算出的數據與試驗數據較吻合，能較好地反映出材料在各個溫度點下的性能，說明該方法切實可行。

3.2 炭纖維/環氧樹脂復合材料擬合數據及分析

針對復合材料隨溫度變化的性能數據，可用基體在不同溫度下的性能及纖維的性能，通過“混合定律”和“Tsai－Hahn準則”來獲取。同樣應用預示模型(3)，以試驗數據為基礎擬合Tr和n，獲取復合材料隨溫度變化下的基本力學性能。

表2是炭纖維/環氧樹脂復合材料在高低溫環境下所擬合出的Tr和n，將擬合曲線與實際實驗數據曲線進行對比，兩者具有較好的吻合性，見圖5和圖6。

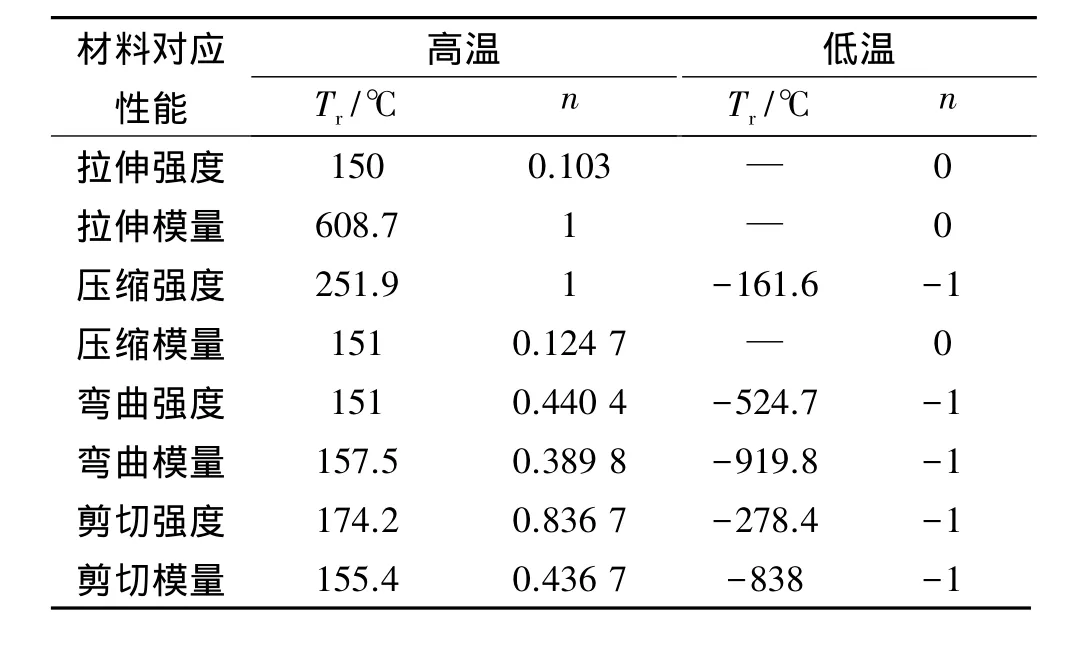
表2 復合材料Tr和n擬合參數Table 2 Fitting parameters of Trand n of composite material

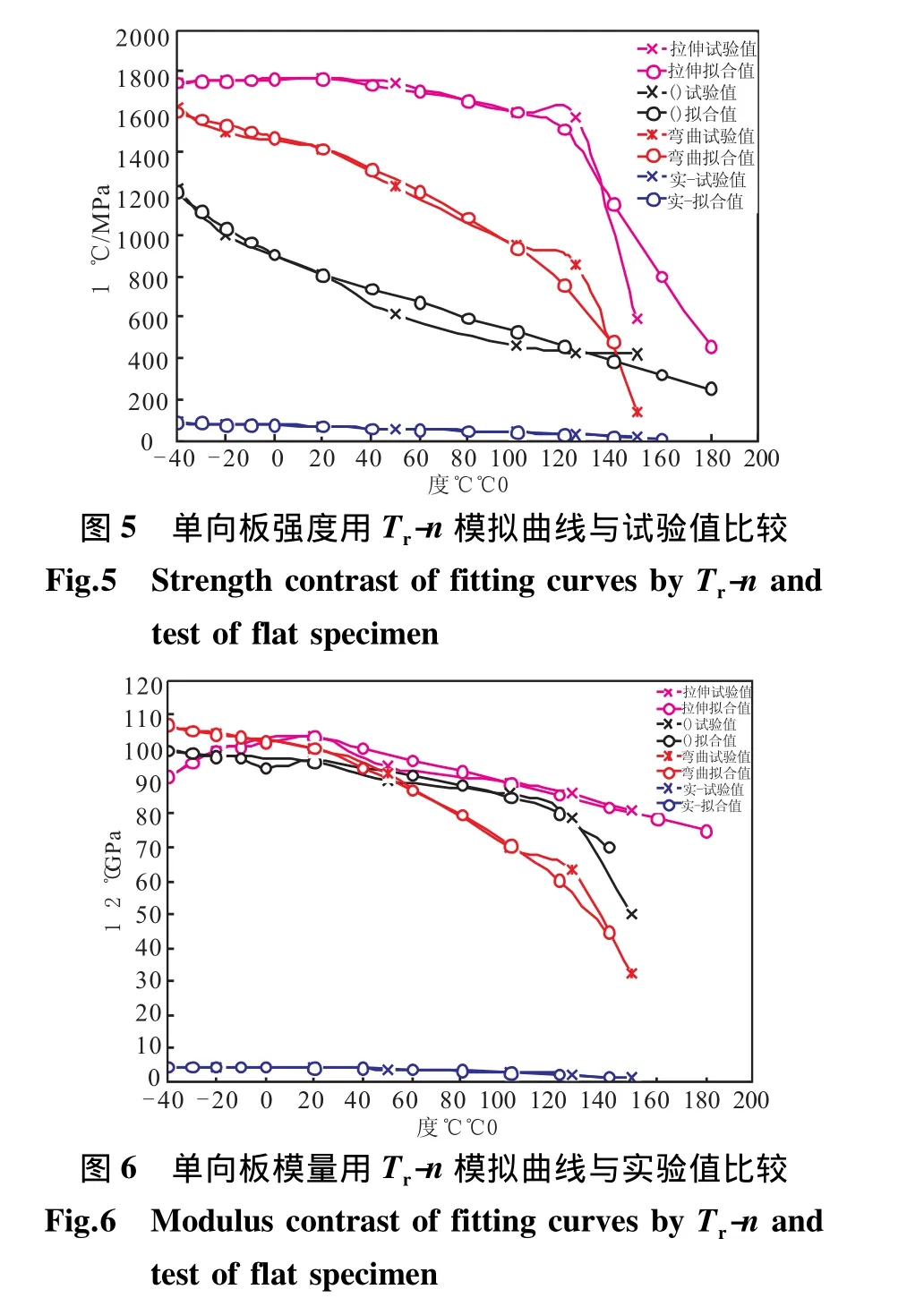
所獲得數據對理論預測復合材料的力學性能隨溫度變化的規律可作為選材的基本依據，對評價和應用復合材料的耐熱性有一定的指導意義。

3.3 復合材料容器擬合數據及分析

目前，固體火箭發動機復合材料殼體結構設計是在經典網格理論的基礎上，依據工程研制及試驗數據，采用系數修正的方法，以適應殼體工作要求為目標推導得出的。該方法是在常溫環境下，在常溫材料參數的基礎上得到的。均衡型纏繞圓筒的爆破壓強可近似由式(5)確定:

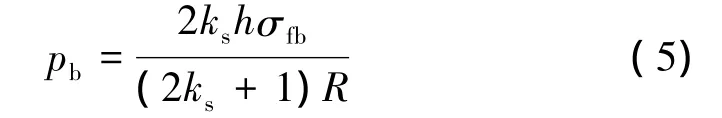
由式(5)可知，h和R均是殼體的結構設計參數，應力平衡系數ks也是與殼體極孔開口大小相關的常系數，以上幾個參數均不受溫度的影響。因此，在溫度影響下，殼體爆破壓強只受纖維材料發揮強度的影響。雖然殼體結構設計是基于經典網格理論，不考慮樹脂基體的性能，但事實上設計所采用的纖維發揮強度是考慮了樹脂基體的影響。同理，通過“混合定律”可知，纖維發揮強度與復合材料、樹脂基體的性能相關。因此，均衡型纖維纏繞殼體隨溫度變化下的爆破壓強也可用式(6)表示:

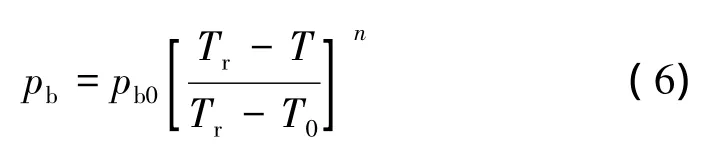
此處，pb0是常溫T0下的爆破壓強，通過 Tr-n模型，可獲得不同溫度下殼體的爆破壓強。但受實驗條件限制，復合材料殼體在高低溫下的爆破試數據采集點較少，無法滿足最小二乘法理論要求。因此，此處不進行試驗數據的擬合對比。

4 結論

(1)提出了炭纖維/環氧樹脂復合材料在溫度影響下的理論預示模型，分析并討論了理論預示模型中的相關參數;建立了滿足環氧樹脂基體材料及炭纖維/環氧樹脂復合材料隨溫度變化的數學模型。

(2)所提出的復合材料受溫度影響力學性能預示方法與實驗結果吻合較好，能獲取材料在任意溫度下的性能變化規律，可作為工程應用中材料設計的計算手段和選材基本依據，對評價和應用復合材料耐熱性有一定的指導意義。

(3)利用網格理論及混合定律，分析了平衡型纖維纏繞復合材料殼體隨溫度變化的規律，擴展到對復合材料殼體爆破壓強的性能預示。

［1］達道安.空間低溫技術［M］.北京:中國宇航出版社，2005.

［2］劉寶鋒，李佩蘭，黎明，等.5231樹脂體系/碳纖維復合材料力學性能研究［J］.高科技纖維與應用，2005，30(6).

［3］李敏，張寶艷.5428/T700復合材料的耐濕熱性能［J］.纖維復合材料，2006(1).

［4］Rock A Rushing.High temperature matrices for filament wound composites［R］.AIAA 2005-3613.

［5］Sung K H，Geoge S S.Mechanical properties of graphite epoxy composites at elevated temperature［R］.ICCM-6 ＆ ECCM-2，1987(4):45-48.

［6］Sung K H，Geoge S S.Nonlinear elastic properties of organic matrix composites at elevated temperatures［J］.Transactions of Thesis，1988(10):13-14.

［7］SAMPE.Simulated data for high temperature composite design［C］//International SAMPE Technical Conference，2004.

［8］李芙蓉.先進復合材料耐熱性評價［D］.北京航空航天大學，1995:35-45.

［9］劉文博，王榮國，張洪濤.CF/PPEK、CF/PPES復合材料高溫力學性能研究［J］.材料科學與工程，2004，12(2):187-188.