交流矢量調速系統繼電反饋PID整定法

康現偉，李 鵬，王勝勇，盧家斌，王國強

（中冶南方（武漢）自動化有限公司，湖北武漢430205）

1 引言

按照偏差的比例（Proportional）、積分（Integral）和微分（Derivative）進行控制的調節器簡稱PID調節器。由于其算法簡便、魯棒性好、可靠性高等優點，PID控制算法被廣泛應用于工業過程控制。

當前工業控制的狀況表明90%以上的控制回路是采用PID控制策略［1]，在石化、化工、造紙等工業領域，甚至有97%的常規控制器都是PID控制器。因此，PID控制器可以視為自動控制的“面包與黃油”。

PID控制器在實際應用時需要進行參數整定。早期的參數都采用手動整定，現場工程師通過一系列調節試驗繪制出過程動態特性曲線或頻率響應曲線，再通過這些曲線由整定公式計算出PID參數。整個整定過程既費時又費力。而且實際生產往往具有非線性、不確定性，難以建立精確的數學模型，常規的PID控制器難以達到理想的控制效果。由于參數整定方法煩雜，常規PID控制器參數往往整定不良、性能欠佳，難以適應復雜環境。針對以上問題，人們一直在研究PID控制器參數的自整定技術，以適應復雜的工況和高性能指標的控制要求。隨著現代電子技術和計算機技術的飛速發展，PID控制器的自整定技術也在近二十年來取得了長足的進步。自整定的發展減少了控制工程師現場調試工作量，節省了大量時間，且整定結果更加可靠，使一些復雜但是更加精細的設計方法能夠應用于實際過程工業控制［2，3]。

本文首先介紹一些常用的整定公式，這些整定公式可以直接應用于PID自整定控制器。詳細分析了繼電反饋自整定方法，并推導出適用于工程的整定公式，將其應用到了交流矢量調速系統的PI參數自整定中。

2 PID參數自整定

在長期的工程實踐中，人們已經積累了大量使用PID控制策略的經驗。尤其是在工業過程控制中，由于控制對象的精確數學模型難以建立，系統參數又經常發生變化，因而運用現代控制理論進行分析、綜合會耗費很大代價進行模型辯識，且往往不能得到預期的效果，所以人們常用PID調節器，并根據經驗進行參數整定。幾十年來，PID控制的參數整定方法和技術處于不斷發展中，特別是近年來，國際自動控制領域對PID控制參數整定方法的研究仍在繼續，許多重要國際雜志不斷發表新的研究成果，PID控制的參數整定方法和技術也處于不斷發展中。

2.1 Z-N參數整定方法

齊格勒-尼柯爾斯（Ziegler-Nichols）在大量實驗的基礎上，于1942年提出了一種實用的參數整定規則，簡稱 Z-N 規則［4～6]。

Z-N法中最常用的是響應曲線法，即在被控對象的輸入端加一個階躍信號，然后測出輸出的階躍響應曲線。如果被控對象既無積分環節，又無共軛復數極點存在，則階躍響應曲線呈S型，如圖1所示。

該曲線的特性可以用測得的延遲時間τ和時間常數T來表征，其相應的數學模型可以式（1）的傳遞函數近似地描述：

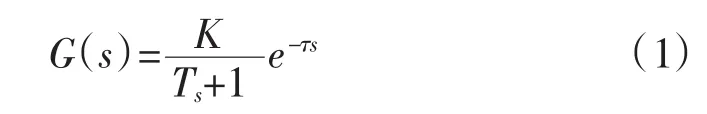
根據實驗測得參數τ、T，再按照表1的規則。即可整定PID控制器的參數。

2.2 繼電反饋法

Asortm和Hagglund在1984年提出基于繼電反饋控制的PID參數整定法。

圖1 階躍響應曲線

表1 響應曲線法整定PID參數

繼電反饋法是在閉環控制回路中加入繼電控制，繼電可以是帶滯后的也可以不帶滯后，利用繼電控制的非線性特性使被控過程出現極限環振蕩，這個振蕩是周期性的，通過測量這個極限環的性質，獲得過程的臨界動態特性參數，即輸出的頻率與振幅，就可以測知對象臨界點的信息，再利用ZN臨界比例度整定公式獲得PID控制器參數［7，8]。

繼電反饋自整定技術有許多突出的優點。首先，這種方法耗時較少且易于使用，操作者只需簡單地按下一個按鍵，即可自動整定出PID控制器參數；其次，繼電反饋自整定調節試驗是閉環進行的，適當選擇繼電參數可以使過程的頻率響應維持在設定點附近，整個過程會處于線性區域，因此繼電反饋自整定方法有可能適用于高度非線性的過程；第三，這種方法不需要先驗知識來選取采樣率，對于一些復雜的自適應控制器尤其有效。該方法簡單、可靠、易于使用，已經廣泛應用于工業PID控制器的參數自動整定。

3 適用于交流矢量調速系統的繼電反饋PID整定法

在實際應用中，原始Z-N法的階躍響應曲線法以及臨界振蕩法容易造成過流或電機失控而導致故障，難以應用到由交流矢量調速系統中，本文將繼電反饋法應用于交流矢量調速系統。

在交流矢量調速系統中，通常都只采用PI控制器，其參數可以通過構建控制系統的傳遞函數模型來計算，但這種方法過于理想化，在構建出的模型里許多參數都采用了近似計算，公式復雜、變量過多導致精度降低，而且在實際的系統中，由于周圍環境和設備自身的物理特性的影響，由控制模型計算出的PI參數往往不能滿足工程應用的需求。繼電反饋法原理簡單，采用的變量較少且易于采集，因此本文將其應用于交流矢量調速系統，整個控制系統如圖2所示。

圖2 采用繼電反饋法的交流矢量調速系統

該系統由轉矩環、磁通環和速度環組成，轉矩環、磁通環實際上是同級的內環（電流環），而速度環則是外環，內外環組成了雙閉環調速系統。對于雙閉環系統，輸出的速度對內環的PI參數不敏感，因此該系統電流環采用傳遞函數計算出PI參數；外環速度環的PI參數直接影響系統的輸出，因此采用繼電反饋法整定PI參數。

在實際的工業過程控制中，繼電控制信號往往是系統執行器的輸入信號，該信號不能為負值。繼電振蕩的PID參數自整定算法的控制過程曲線如圖3所示。被控對象只要在高頻具有至少-π的相位之后就可在繼電反饋狀態下產生周期為T的等幅振蕩，而其頻率正是使被控對象相位滯后-π的頻率，即奈氏曲線與負實軸焦點的頻率ωn。設繼電特性幅值為d，被控對象的輸出為y（設被控對象振幅為a），由傅里葉級數展開繼電特性輸出可知，在臨界頻率ωn處的幅值近似為：

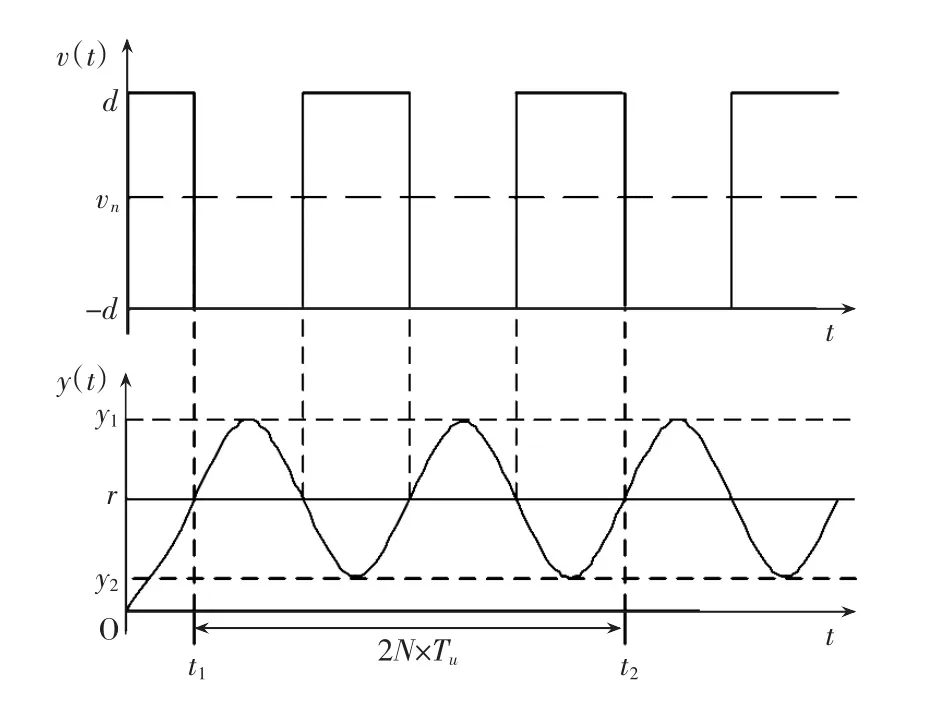
圖3 自整定過程曲線

在實際測量時，為了消除環境以及被控對象物理特性的干擾，得到穩定的振蕩波形，從第二個周期開始采樣，截取N個完整的振蕩周期，由圖3可求出振幅A與振蕩周期Tu，測量公式為：

其中：A為系統輸出的振幅，Tu為臨界振蕩周期，y1為實際輸出速度的波峰值，y2為波谷值，t1和t2分別是采樣開始時間和結束時間。在測得A和Tu后，根據原始Z-N法中的臨界振蕩法，可以推得：

由式（2）～（6）可以推導出：

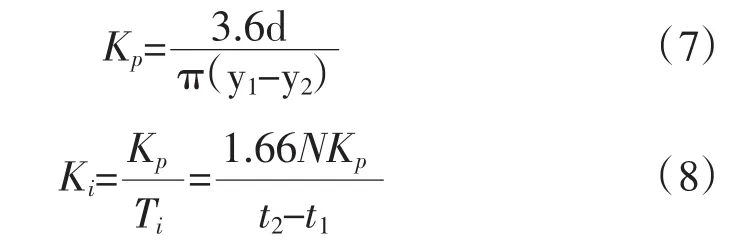
其中：d是實際輸入目標值，即為給定的速度階躍信號振幅。

4 PI參數整定實驗及結果

實驗采用的平臺為變頻器（CPU為TI的F2812 DSP）控制的對拖機組（7.5kW交流異步電機和作為負載的同軸直流電機），程序運行于DSP中。

進行兩個實驗，首先采用閉環繼電振蕩法整定PI參數，再采用原始Z－N法（臨界振蕩）計算出另一組PI參數。然后分別采用這兩組PI參數對電機進行階躍響應實驗和穩速運行實驗，記錄相應的實驗參數并加以比較。

4.1 PI整定實驗

閉環繼電反饋整定程序流程。

（1）通常繼電振蕩實驗需在0頻附近振蕩，即振蕩中線頻率為0Hz，但為了測量，此處設定圖3中振蕩中線頻率vn為15Hz。由于是采用的是閉環繼電振蕩，因此實際振幅比設定值通常要小很多，為了便于采樣及提高計算精度，采用了較大的振幅給定值15。

（2）先給交流電機通勵磁電流，等待一個直流磁化時間（即磁場建立所需要的時間，約等于轉子時間常數），給電機輸入一個30Hz的速度階躍給定值。

（3）當電機速度達到vn時，立即將輸入給定值設為0Hz的階躍信號，此時由于慣性電機的轉度仍會繼續升高，到達峰值y1后就會減速。

（4）當電機速度下降為vn時，立即將輸入給定值重新設為30Hz的階躍信號，此時電機速度會先減小至y2，然后會開始加速。

（5）重復步驟3、4直到產生穩定的速度振蕩（即多次y1的測量值都相同）并開始采樣，當采集到N個完整振蕩周期后停機。

（6）根據式（7）、（8）計算出速度環 PI參數。

圖4所示為連續整定過程，需要注意的是，本文所介紹的方法是在閉環狀態下進行的，需對電機安裝編碼器。

采用原始Z－N法（臨界振蕩）整定出的PI參數的方法較為常見，大多數教科書上都有介紹，因此這里不再贅述。

圖4 變頻器閉環繼電反饋自整定過程曲線

4.2 性能比較實驗

對兩種方法整定出的參數分別施加10Hz的速度階躍信號，其實驗結果如圖5所示。對于穩速運行狀態，兩種方法的速度脈動曲線如圖6所示，其中縱坐標為額定頻率的百分比，20%為10Hz。兩種方法整定出的參數對比如表2所示。

圖5 速度階躍響應曲線

圖6 速度脈動（縱坐標為額定頻率50Hz的百分比）

表2 兩次自整定結果

由實驗結果可知，繼電反饋法可以良好地應用于實際的交流矢量調速系統中，其整定效果遠好于原始Z－N法，其主要優點有：

（1）整定時間短。由圖4可以看到，整個閉環繼電反饋整定過程不超過1s，極大地提高了PI參數的設置效率。

（2）整定后動態性能好。由圖5和表2可知，與傳統的Z－N法相比，通過繼電反饋整定的PI參數上升和穩定時間短、超調量小，具體參數見表2。

（3）穩速運行時脈動小且波形穩定。由圖6可以看到，繼電反饋法整定出的PI參數在穩速運行時脈動很小，其速度波形規則、穩定，而Z－N法的速度波形則顯得較為雜亂且有小幅波動。

5 結論

本文介紹了PID參數自整定的幾種方法，并將繼電反饋法按工程應用的需求加以簡化，為了保護電機，將該方法改進為閉環下使用，減小了電機在整定時轉速的實際振幅，將該方法應用于實際的交流矢量調速系統中。實驗結果表明，采用繼電振蕩法取得了良好的整定效果，大大提高了變頻器調節PI參數的效率及準確性，解決了實際工程中PI參數的整定基本靠手動調節的問題。

［1] Astrom.K.J，Hagglund，T.PID Controllers：Theory，Design and Tuning.Instrument Society of America，1995.

［2] 曹承志.微型計算機控制新技術［M] .北京：機械工業出版社，2001.150－165.

［3] 陶永華.PID控制原理和自整定策略［J] .工業儀表和自動化裝置，1997，（4）：60－64.

［4] 王 偉，張晶濤，柴天佑.PID參數先進整定方法綜述［J] .自動化學報，2000.26：347－355.

［5] 張晉格.控制系統CAD－基于MATLAB語言［M] .機械工業出版社，2004，162－164.

［6] 錢積新，王 慧，周立芳.控制系統的數字仿真及計算機輔助設計［M] .北京：化學工業出版社，2003.132－136.

［7] 謝元旦，夏淑艷.PID調節器參數的繼電自整定方法［J] .控制與決策，1993，8（1）：77－79.

［8] 楊 智.自整定PID調節器設計方法［J] .甘肅工業大學學報，1998，24（1）：79－81.