基于仿生小波變換和模糊推理的語音降噪算法研究

左東廣，王偉軍，樊天鎖，周 帥，張欣豫

（第二炮兵工程大學 陜西 西安 710025）

在語音通信中，不可避免的會受到各種噪聲的干擾，較大的噪聲信號可以使語音處理系統的性能急劇下降，甚至處于癱瘓狀態。由于語音信號和噪聲信號和噪聲信號都是非平穩時變的隨機信號[1]，使得固定步長的自適應LMS算法在提高初始收斂速度和提高濾波精度上存在不可調和的矛盾，越來越多的變步長LMS算法應用于信號降噪處理中[1-2]。

文中以模糊推理和仿生小波變換為基礎，提出了一種新的自適應變步長LMS算法對語音信號進行降噪處理。該算法能夠實現在大的誤差范圍內步長較大，小的誤差范圍內步長較小，并結合仿生小波變換對語音信號噪聲的良好分解能力，達到對語音信號進行濾波的目的。該算法具有較高的收斂精度和良好的跟蹤躍變系統能力，實現了非平穩的語音信號在同頻段對噪聲信號和語音信號的最佳估計和信噪分離。為語音信號的降噪處理技術提供了一種新的方法。

1 基于模糊推理的步長自適應調整算法（VS-FLMS）

語音信號的噪聲消除可以通過自適應濾波器實現[3]。自適應濾波的算法有很多，基本的方法有最小均方誤差算法（LMS）和遞歸最小二乘（RLS）算法[4]。步長因子 μ（n）的變化的基本原理是：當誤差|e（n）|較大時，步長 μ（n）較大，當|e（n）|較小時，步長μ（n）也變小。這種原則類似于模糊推理的原則，因此可以將模糊推理技術應用于變步長算法的改進。

考慮采用帶有中心平均解模糊器、乘積推理機、單值模糊器及高斯隸屬函數的模糊推理系統，其在理論上是一個萬能的逼近器，能夠逼近任意精度的函數。可以通過一個雙規則模糊控制系統來說明對步長因子μ（n）的調整過程。

在模糊控制系統中，絕對誤差|e（u）|看作模糊控制系統的輸入信號，步長因子M（m）作為模糊控制系統的輸出信號。以下兩條規則構成了模糊推理系統。

規則 A：如果|e（n）|較大，則 μ（n）較大；

規則 B：如果|e（n）|較小，則 μ（n）較小。

為了書寫方便，用 x 代替|e（n）|，用 y 代表 μ（n）。 模糊集“較大”與“較小”的兩個隸屬度函數分別表示為：

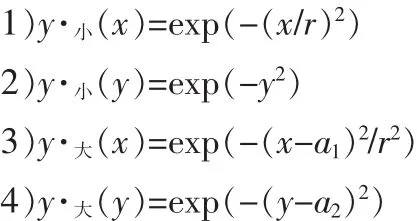
式中a1a2＞0，通過中心平均解模糊器和乘積推理機，可以得到模糊控制系統如下：

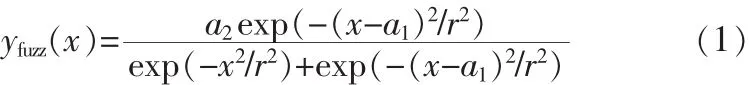
化簡后，得到：

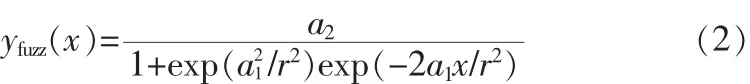
將|e（n）|和 μ（n）代入式（2）后化簡得到：

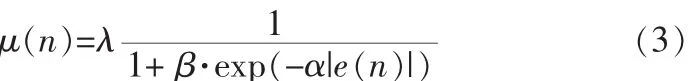
將式（3）中的|e（n）|改為 e（n）2對總體運算不產生太大影響，可得 μ（n）與 e（n）的函數關系式為：

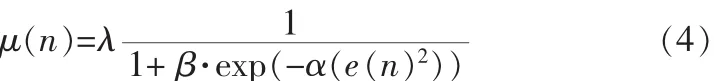
式（4）中 β 用于調節 μ（n）的最小值，α 用于調節 μ（n）與e（n）曲線的傾斜度，λ 用于調節 μ（n）的最大值。

根據萬能逼近原理[5]，只要選擇恰當的隸屬度函數和模糊原則，就可以得出μ（n）與e（n）的非線性函數表達式，用任意的精度去逼近一切 μ（n）與 e（n）的連續性函數，保證了VS-FLMS算法的收斂速度和收斂精度。

2 仿生小波變換法

在對語音信號進行處理的過程中考慮人耳對語音信號的感知特性[6]。小波分解過程中結合人耳的臨界帶寬并不能較好地反映人耳對語音信號的幅度以及頻率的感知特性，考慮采用仿生的小波變換法[7]進行語音信號的信噪分離。

仿生小波變換（BWT）是將人耳的耳蝸機理和小波變換相結合的一種基于生物模型的自適應時頻分析方法。相比于一般的小波變換，它在時頻域的尺度不僅可以根據信號的頻率進行調節，還可以隨著信號的瞬時幅度以及一階微分系數自適應調節。在一般的小波變換中[8-9]，母小波函數h（t）必須滿足容許條件，因此可以用其包絡函數（t）來表示，即

式中 ω0=2πf0，f0為 h（t）的窗中心頻率。 信號 f（t）的小波變換為：

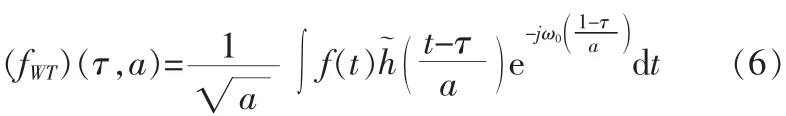
式中a與τ分別表示尺度和時間因子。仿生小波變換引入調整因子T到小波變換的母函數中[10]，即：

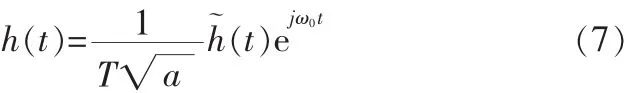
其中調整因子T是Gigure的主動聽覺模型引入的，它的定義為：

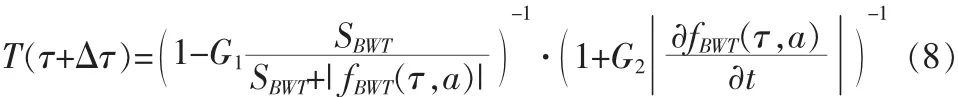
式中fBWT（τ，a）表示時間 τ與尺度 a下的仿生小波系數，G1與G2分別表示人耳中耳蝸的兩個能動因子，SBWT表示為飽和因子，Δτ表示計算步長，仿生小波變換可表示為：

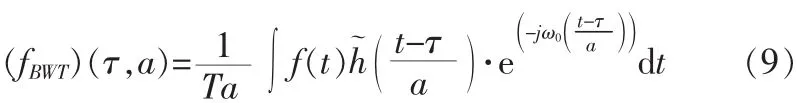
仿生小波變換比一般的小波變換具有明顯的優點，但是調整因子的公式過于復雜，降低了該算法的實時跟蹤能力。通過對Morlet母小波的研究，表明仿生小波變換與基本小波變換之間存在以下的關系：

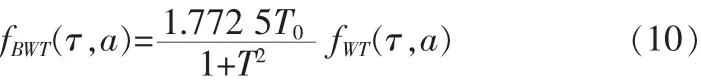
式中 fBWT（τ，a）表示仿生小波變換的系數，fWT（τ，a）表示一般的小波變換的系數，T0表示母小波函數的常量。

3 基于仿生小波變換和模糊推理變步長自適應濾波語音降噪算法

用小波變換法區分有用信號和噪聲信號的方法有很多[13]，主要有：基于小波變換的模的極大值原理消噪法、小波閾值消噪法以及基于小波變換域內系數相關性消噪等[11]，但是當有用信號和噪聲信號在重疊頻譜時，這些方法雖然能實現信噪分離，提高信噪比，但是不能實現對噪聲信號的最優估計，很難實現最優濾波。文中結合模糊推理與仿生小波變技術，提出了基于仿生小波變換和模糊推理變步長自適應濾波語音降噪處理算法，其模型如圖1所示。

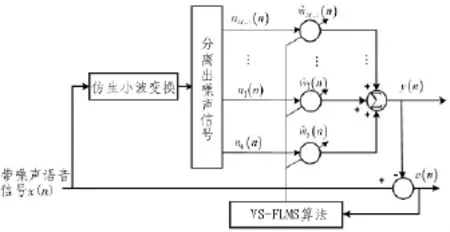
圖1 算法結構模型Fig.1 Algorithm structure model

圖中 N=[n0，n1，…，nM-1]T表示輸入信號 x（n）經過仿生小波變換法分離出來的噪聲分量，M表示濾波器的階數。算法的主要流程如下：

1）對含噪聲的語音信號x（n）進行仿生小波變換

對含噪聲的語音信號進行預處理后，進行仿生小波變換，得到含噪聲的小波系數。

設 x（n）=s（n）+v0（n），式中 x（n）表示含噪聲 語音信號，s（n）表示語音信號，v0（n）表示噪聲信號。 含噪聲語音信號經過仿生小波變換后，得到：

式中fBWTT為含噪聲語音信號經過仿生小波變換的系數。

經過仿生小波變換后，有用的語音信號表現為低頻信號，噪聲信號為高頻信號，通過閾值處理的方法去掉低頻信號，保留高頻的噪聲信號，作為自適應抵消器的輸入信號。仿生小波變換的原理框圖如圖2所示。

圖2 仿生小波變換的原理圖Fig.2 Schematic of the bionic wavelet transform

利用小波閾值處理方法的基本步驟如下：

①對語音信號進行一維的分解：選擇一個小波，同時確定分解的層次J，然后對語音信號進行J層分解。

②小波分解高頻系數的閾值壓縮，選擇恰當的閾值和閾值函數，對第一層到第J層的高頻系數進行閾值壓縮，分解出其中的噪聲成分。閾值的取值為：

2）對分解后的小波系數進行基于模糊推理的變步長自適應濾波

自適應濾波器的輸入信號為 N=[n0，n1，…，nM－1]T，濾波器的輸出信號為：

誤差信號為：

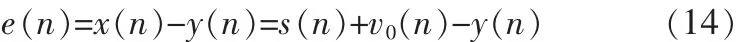
均方誤差LMS算法的迭代公式為：

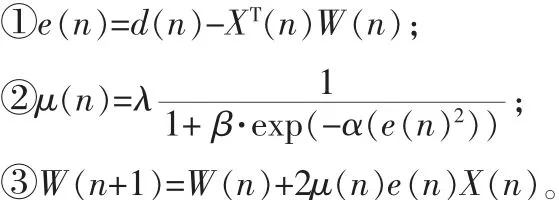
將式①代入②、③可得：

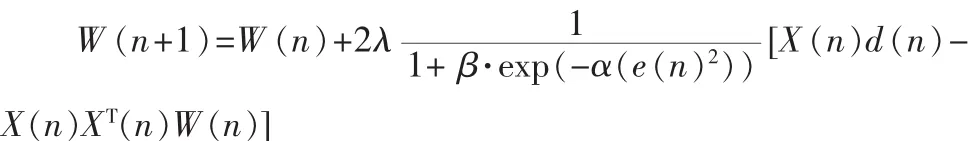
當誤差信號的均方值最小時，即E[e2（n）]最小時，輸出信號e（n）逼近語音信號 s（n），通過上式不斷調整濾波器的抽頭權值，使E[e2（n）]達到最小，這時濾波器的權系數即為最佳權值。

4 實驗驗證和結果分析

實驗中采用Morlet函數作為仿生小波的母小波，漢寧窗為窗函數，變換尺度設為a=20，取T0=0.000 073 28，G1=0.62，G2=72.84，自適應濾波器 M=16，μ=0.005。

在語音庫中截取一段基本的語音信號作為樣本，采樣頻率為 16 kHz，加入高斯白噪聲 v0（n）（0，），通過調整噪聲的方差來調整輸入信號的信噪比，范圍在－5～5 dB。信噪比為－5 dB時的仿真結果如圖3所示。

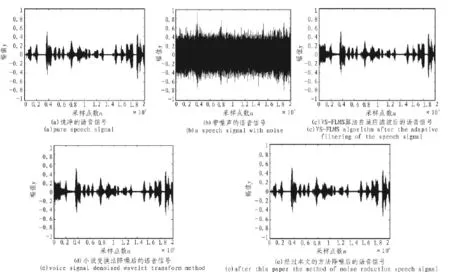
圖3 語音降噪效果對比圖Fig.3 Voice Noise Reduction effect comparison chart

表1給出了信噪比為－5～5 dB的含噪聲語音信號經過3種降噪方法后的信噪比情況。

其失調量的對比圖如圖4所示。

通過圖3中的3種降噪處理方法和表1的數據的對比，文中提出的降噪處理方法明顯地優越于其他2種方法，信噪比有很大的提高，文中的方法比單一的自適應濾波法和仿生小波變換法的信號降噪效果都為明顯，表明了該算法在語音降噪處理方面的效果是很明顯的。

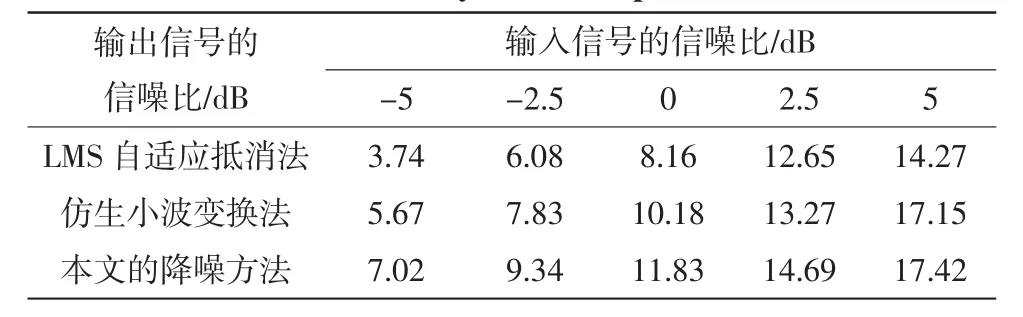
表1 3種方法的信噪比對比圖Tab.1 Three ways SNR comparison chart

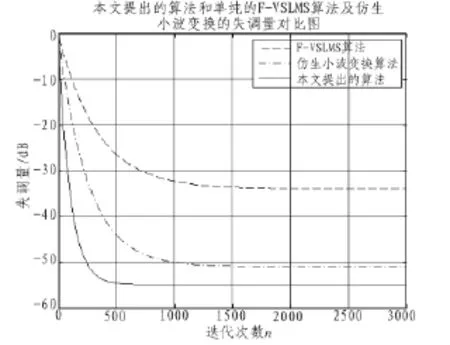
圖4 失調量對比圖Fig.4 Comparison chart of the offset amount

5 結 論

文中通過仿生小波變換對語音信號進行信噪分離，將其輸出作為模糊推理變步長自適應濾波器的輸入進行語音信號的降噪處理，提出了一種基于仿生小波變換與模糊推理變步長自適應濾波器的語音降噪算法。該算法具有較高的收斂精度和良好的跟蹤躍變系統能力，實現了非平穩的語音信號在同頻段對噪聲信號和語音信號的最佳估計和信噪分離。為語音信號的降噪處理技術提供了一種新的方法。

[1]趙力.語音信號處理[M].2版.北京：機械工業出版社，2010：63-68.

[2]孫恩昌，李于衡，張冬英，等.自適應變步長LMS濾波算法及分析[J].系統仿真學報，2007，19（4）:3172-3175.

SUN En-chang，LI Yu-heng，ZHANG Dong-ying，et al.Variable step size LMS adaptive filtering algorithm and analysis[J].Journal of System Simulation，2007，19（4）:3172-3175.

[3]曹斌芳，李建奇.強噪聲背景下的語音信號提取研究[J].噪聲與振動控制，2008，28（4）:145-148.

CAO Bin-fang，LI Jian-qi.Voice signal extraction in the context of strong noise[J].Noise and Vibration Control，2008，28（4）:145-148.

[4]Haykin S.Adaptive filter theory[M].Fourth Edition.北京：電子工業出版社，2006:342-347.

[5]陸光華，彭學愚，等.隨機信號處理[M].西安：西安電子科技大學出版社，2003:163-167.

[6]韓紀慶，張磊，鄭鐵然.語音信號處理[M].北京：清華大學出版社，2004:54-57.

[7]龔亮，張艷萍.基于掩蔽效應的改進型自適應語音增強算法[J].南京信息工程大學學報：自然科學版，2010，2（6）:529-532.

GONG Liang，ZHANG Yan-Ping.Based on the masking effect of improved adaptive speech enhancement algorithm[J].Nanjing University of Information Science and Technology：Natural Science，2010，2（6）:529-532.

[8]Chen S H，Wang J F.Speech enhancement using perceptual wavelet packet decomposition and eager energy operator[J].Journal of VLSI Signal Processing，2004，36（2）:125-139.

[9]Loizou H Y，Philipos C.Speech enhancement based on wavelet threshold the multilayer spectrum[J].IEEE Trans on Speech and Audio Processing，2004，12（1）:59-67.

[10]楊璽，樊曉平.基于仿生小波變換和自適應閾值的語音增強方法[J].控制與決策，2006，21（9）:1033-1036.

YANG Xi，FAN Xiao-ping.Bionic wavelet transform and adaptive threshold-based voice enhancement method[J].Control and Decision，2006，21（9）:1033-1036.

[11]張曉寧，孫麗君.一種改進的小波閾值信號去噪方法[J].電子科技，2012（11）：15-17，24.

ZHANG Xiao-ning，SUN Li-jun.An improved method for wavelet threshold signal demonizing[J].Electronic Science and Technology，2012（11）：15-17，24.