一種基于狀態(tài)反饋的位置控制算法研究

曾 輝 富春巖 李川匯 李 俊 陳春蕾

（佳木斯大學(xué) 黑龍江佳木斯 154007）

在隔震裝置的性能研究中，一般采用地震模擬實(shí)驗(yàn)的方法，地震模擬實(shí)驗(yàn)臺多數(shù)是通過機(jī)械振動(dòng)的方式模擬地震波，目前性能比較穩(wěn)定的是液壓式模擬實(shí)驗(yàn)臺[1]。實(shí)驗(yàn)臺一般采取伺服閥（比例閥）控液壓缸來實(shí)現(xiàn)振動(dòng)模擬[2]。本文運(yùn)用基于狀態(tài)反饋的電液比例控制方法，通過這種控制方法，提高了振動(dòng)模擬裝置的系統(tǒng)動(dòng)態(tài)性能，縮短了系統(tǒng)的滯后時(shí)間，減少了系統(tǒng)振蕩和超調(diào)，增強(qiáng)了系統(tǒng)的動(dòng)態(tài)穩(wěn)定性。

一、控制系統(tǒng)的方框圖

根據(jù)震動(dòng)模擬裝置伺服閥的力學(xué)模型和數(shù)學(xué)模型得到傳遞函數(shù)為[3]：

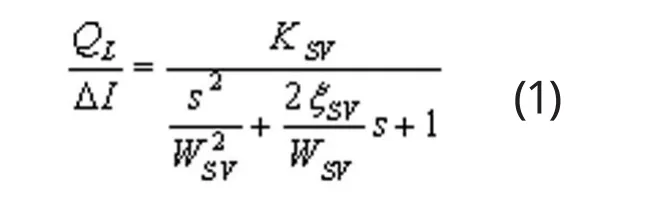
伺服比例系統(tǒng)的方框圖如圖2所示。

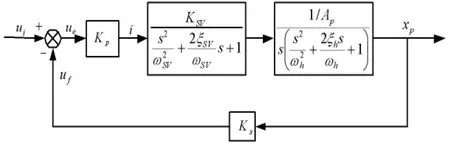
圖2 震動(dòng)模擬裝置伺服比例系統(tǒng)方框圖

二、系統(tǒng)的能控性和能觀性

（一）控制系統(tǒng)的狀態(tài)空間表達(dá)式

根據(jù)系統(tǒng)方框圖得到控制系統(tǒng)的傳遞函數(shù)為：

由公式(2)得到控制系統(tǒng)矩陣為：

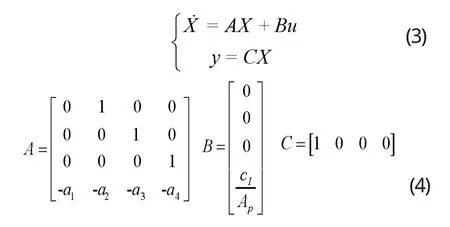
（二）系統(tǒng)的能觀能控性

(1)將系統(tǒng)參數(shù)代入控制矩陣得到能控性矩陣為：

由式(5)可知，系統(tǒng)的能控性矩陣特性為滿秩，由此可知該系統(tǒng)為完全能控。

(2)系統(tǒng)的能觀測性矩陣為：

由式(6)可知，系統(tǒng)的能觀測性矩陣特性為滿秩，由此可知該系統(tǒng)為完全能觀。

三、控制系統(tǒng)狀態(tài)反饋及狀態(tài)觀測器的構(gòu)造

（一）振動(dòng)模擬裝置控制系統(tǒng)的極點(diǎn)選取

根據(jù)控制系統(tǒng)方塊圖在MATLAB軟件中建立仿真模型如圖3所示。

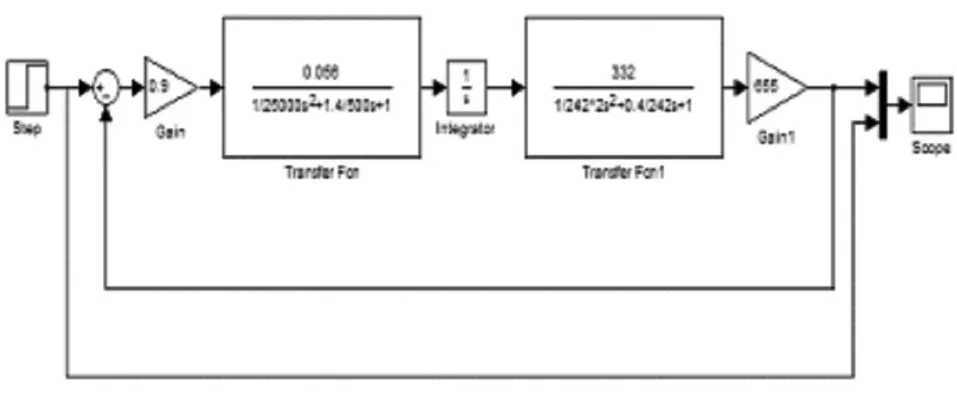
圖3 振動(dòng)模擬裝置MATLAB仿真模型

系統(tǒng)在階躍信號輸入時(shí)的響應(yīng)曲線MATLAB仿真曲線如圖4所示，為了進(jìn)一步提高系統(tǒng)的性能，滿足隔震模擬實(shí)驗(yàn)所需振動(dòng)輸出信號輸出的要求，應(yīng)用觀測器和極點(diǎn)配置的控制方法對系統(tǒng)進(jìn)行優(yōu)化設(shè)計(jì)，圖中為上升時(shí)間[4]。

圖4 階躍信號輸入下的控制系統(tǒng)響應(yīng)曲線

根據(jù)圖4選取期望的極點(diǎn)，求得期望極點(diǎn)為 ：-112.379505，-112.379505，-160.5506，-160.5506。

（二）振動(dòng)模擬系統(tǒng)狀態(tài)反饋矩陣K的設(shè)計(jì)

系統(tǒng)的能控標(biāo)準(zhǔn)型變換矩陣如下所示：

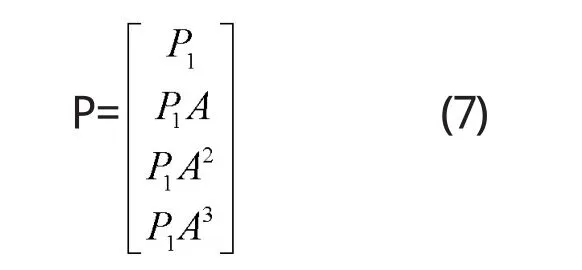
由此可得到：

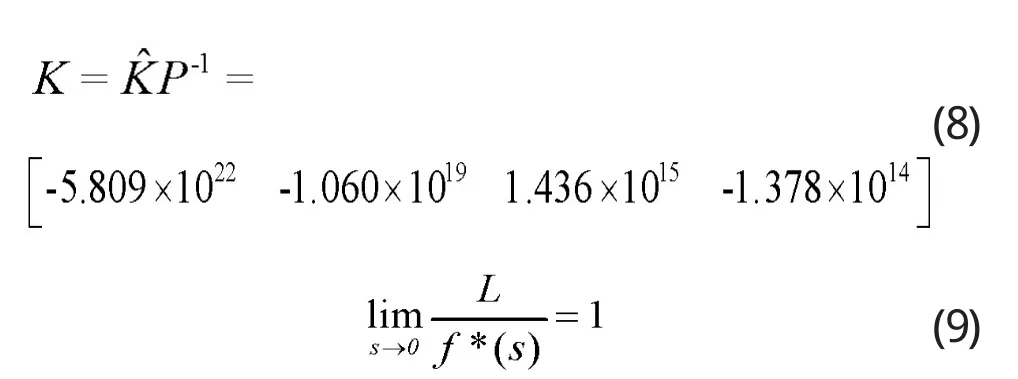
由式(9)求得 L=1048756。

（三）狀態(tài)觀測器的設(shè)計(jì)

分析系統(tǒng)的能觀矩陣，因該控制系統(tǒng)為完全能觀測，系統(tǒng)的完全能觀測矩陣為：

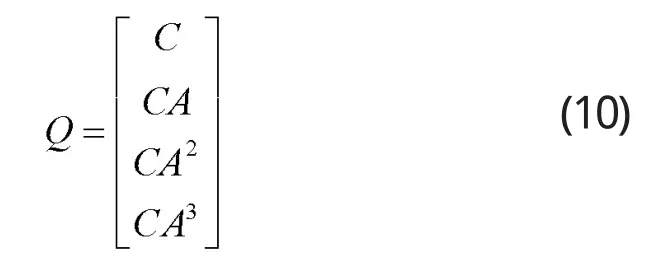
將系統(tǒng)狀態(tài)方程及輸出方程轉(zhuǎn)化為能觀測規(guī)范型，變換矩陣T有：

則得到系統(tǒng)能觀測規(guī)范型為：

（四）控制系統(tǒng)狀態(tài)觀測器的特征方程分析

根據(jù)極點(diǎn)配置的要求S1-112.37965，S2-112.37965，S3-160.5506，S4-160.5506建立與之對應(yīng)的特征多項(xiàng)式：

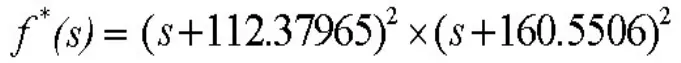
由于以上的兩個(gè)特征多項(xiàng)式對應(yīng)項(xiàng)系數(shù)相等，比較可得對應(yīng)系統(tǒng)規(guī)范型的反饋矩陣，并得到給定控制系統(tǒng)狀態(tài)方程的反饋矩陣G：

系統(tǒng)觀測器方程為：

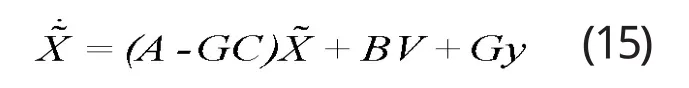
帶觀測器的振動(dòng)模擬系統(tǒng)狀態(tài)反饋系統(tǒng)方塊圖如圖4所示。

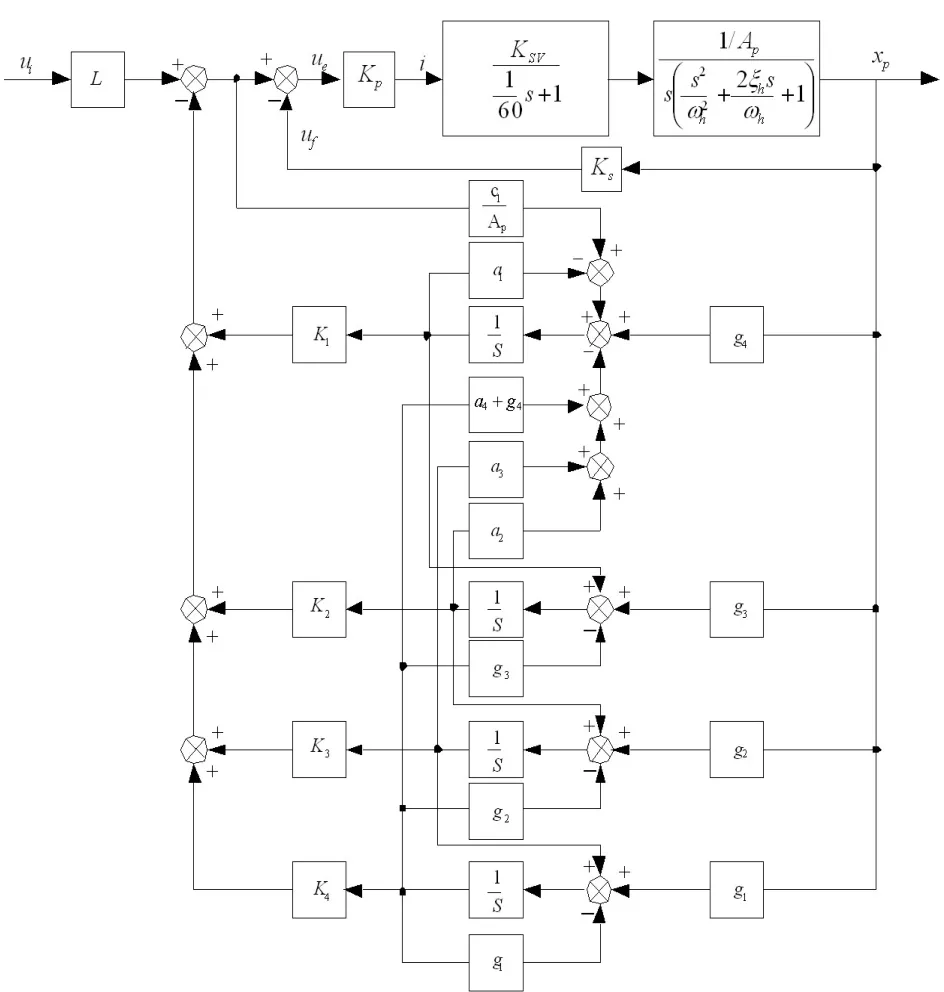
圖4 帶觀測器的狀態(tài)反饋系統(tǒng)方塊圖

四、振動(dòng)模擬控制系統(tǒng)仿真曲線分析

為了檢驗(yàn)應(yīng)用系統(tǒng)狀態(tài)反饋與選取狀態(tài)觀測器的控制方法時(shí)的系統(tǒng)性能，運(yùn)用工程模擬中比較常用的MATLAB仿真軟件搭建仿真模型，對系統(tǒng)進(jìn)行了仿真分析。其中圖5為直接運(yùn)用PID控制的系統(tǒng)階躍響應(yīng)仿真曲線。圖6為加入狀態(tài)觀測器的系統(tǒng)階躍響應(yīng)仿真曲線。

圖5 PID控制的階躍響應(yīng)仿真曲線

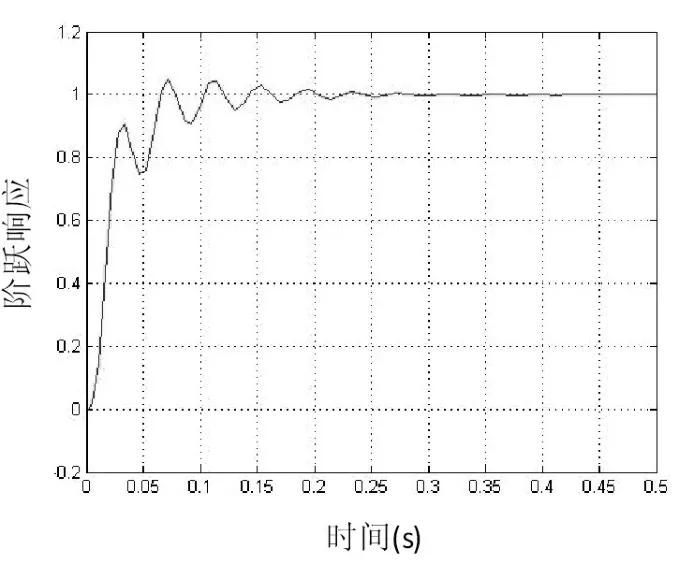
圖6 加入狀態(tài)反饋的階躍響應(yīng)仿真曲線

階躍信號的系統(tǒng)響應(yīng)曲線表明，針對控制系統(tǒng)的極點(diǎn)，在控制系統(tǒng)系統(tǒng)中加入了狀態(tài)觀測器，是系統(tǒng)的超調(diào)量減小，響應(yīng)時(shí)間縮短。控制系統(tǒng)能夠達(dá)到隔震實(shí)驗(yàn)的精確控制要求。

實(shí)驗(yàn)表明，由于在振動(dòng)模擬控制系統(tǒng)中加入了狀態(tài)反饋的控制方法，通過極點(diǎn)配置，提高了振動(dòng)模擬裝置動(dòng)態(tài)負(fù)載情況下的快速性，降低了控制系統(tǒng)超調(diào)，滿足了振動(dòng)模擬裝置在高頻、大強(qiáng)度、重載荷和動(dòng)態(tài)負(fù)載等復(fù)雜工況下的系統(tǒng)輸出穩(wěn)定性要求。

[1]隋莉莉，歐進(jìn)萍.MR減振驅(qū)動(dòng)器用于結(jié)構(gòu)振動(dòng)控制的算法研究[J].應(yīng)用力學(xué)學(xué)報(bào)， 2002,19(3):143-148.

[2]劉玉蘭，祁桂蘭.基于狀態(tài)反饋極點(diǎn)配置隨動(dòng)系統(tǒng)的設(shè)計(jì)與實(shí)現(xiàn)[J].制造業(yè)自動(dòng)化，2009,11(31):76-78.

[3]李書，孫忠凱，向錦武.結(jié)構(gòu)控制中輸出反饋魯棒極點(diǎn)配置優(yōu)化方法 [J].力學(xué)學(xué)報(bào)，2001,1(33):71-78.

[4]段廣仁，吳廣玉，黃文虎.線性系統(tǒng)的狀態(tài)反饋特征結(jié)構(gòu)配置 [J].自動(dòng)化學(xué)報(bào)，1990,11(16):566-568.