運(yùn)用縱橫二維框架比較中新教科書(shū)中“勾股定理”

章健楠，葉立軍

目前，新加坡已經(jīng)逐步形成穩(wěn)定的、具有自身特色的數(shù)學(xué)課程體系，[1]對(duì)于同處于東亞地區(qū)、與其文化背景極為相似的中國(guó)來(lái)說(shuō)，比較、研究中新兩國(guó)數(shù)學(xué)教材，有利于取長(zhǎng)補(bǔ)短，同時(shí)也能夠?yàn)閿?shù)學(xué)教育打開(kāi)新思路。本文選用Charalambos Y.Charalambous等在文[2]中建立的縱橫二維研究框架，對(duì)人民教育出版社的《數(shù)學(xué)》（以下簡(jiǎn)稱(chēng)人教版教材），[3]以及新加坡Multimedia Communications Press出版社出版的New Express Mathematics（以下簡(jiǎn)稱(chēng)NEM教材）[4]中的“勾股定理”進(jìn)行比較研究。

一、研究背景

（一）選取“勾股定理”的理由

勾股定理作為幾何學(xué)中的一顆明珠，是整個(gè)平面幾何的基礎(chǔ)，在現(xiàn)實(shí)生活中也被廣泛應(yīng)用。在教材編排中，勾股定理被安排在初中八年級(jí)教材中。此時(shí)正值學(xué)生由具體思維向形式化思維轉(zhuǎn)變的時(shí)期。而在“勾股定理”這一章中，學(xué)生通過(guò)學(xué)習(xí)勾股定理及其逆定理的發(fā)現(xiàn)、證明與應(yīng)用等內(nèi)容，將接觸到數(shù)形結(jié)合、轉(zhuǎn)化等多種數(shù)學(xué)思想方法，為之后形成良好的形式化思維打下基礎(chǔ)。

（二）所選取的研究重點(diǎn)

在本文所比較的兩本教材中，都淡化了勾股定理的證明過(guò)程。兩本教材中關(guān)于“勾股定理的應(yīng)用”部分的內(nèi)容均占據(jù)了相當(dāng)大的比重，NEM教材更是將“運(yùn)用兩個(gè)定理解決實(shí)際問(wèn)題”單獨(dú)列為一個(gè)小節(jié)的內(nèi)容。因此本文將研究重點(diǎn)放在了本章中的應(yīng)用部分（即習(xí)題、范例）上，而非對(duì)每個(gè)知識(shí)點(diǎn)及證明方法的具體分析。

（三）所研究的問(wèn)題

根據(jù)所選取的研究重點(diǎn)，本文將運(yùn)用縱橫二維研究框架建立編碼系統(tǒng)，通過(guò)分析、比較習(xí)題、范例、知識(shí)點(diǎn)編排順序等內(nèi)容，來(lái)研究?jī)杀窘滩膶?duì)于“勾股定理”這一章節(jié)的內(nèi)容呈現(xiàn)方式上有何異同點(diǎn)，以及教材對(duì)學(xué)生的期望分別是什么。此外，基于問(wèn)題的所得出的結(jié)論，作者還將對(duì)兩國(guó)教材的編寫(xiě)做一些思考。

二、研究框架及編碼

（一）研究框架

Charalambos Y.Charalambous等將目前國(guó)際上常用的兩種教材分析方法---橫向比較與縱向比較結(jié)合在一起，建立起一種新的二維研究框架。在這一結(jié)構(gòu)中，橫向包括背景信息和整體結(jié)構(gòu)2個(gè)部分，縱向包括與學(xué)生交流、對(duì)學(xué)生的要求、聯(lián)系3個(gè)部分。[5]

（二）編碼系統(tǒng)

1.橫向維度（見(jiàn)表格 1）

表1

2.縱向維度（見(jiàn)表格 2）

表2

縱向維度建模思維·數(shù)形結(jié)合思想·轉(zhuǎn)化思想·方程思想對(duì)學(xué)生的要求認(rèn)知要求·記憶型(任務(wù)需要對(duì)之前學(xué)過(guò)的知識(shí)，如等邊三角形性質(zhì)、等腰三角形性質(zhì)、三角形的面積計(jì)算公式作簡(jiǎn)單回憶，不需要理解)·有聯(lián)系型程序（任務(wù)集中在選擇解決問(wèn)題的程序上，與概念理解相關(guān)）·做數(shù)學(xué)（任務(wù)并未暗示可以預(yù)期的解題途徑，需要將具體現(xiàn)象上升為本質(zhì)聯(lián)系，進(jìn)行復(fù)雜的思考，設(shè)計(jì)方案解決問(wèn)題。如勾股定理在實(shí)際生活中的應(yīng)用）作答類(lèi)型·只要求一個(gè)答案（數(shù)值或數(shù)值表達(dá)式）·答案或數(shù)學(xué)陳述·推理論證

（三）指標(biāo)的度量

1.橫向維度指標(biāo)的度量

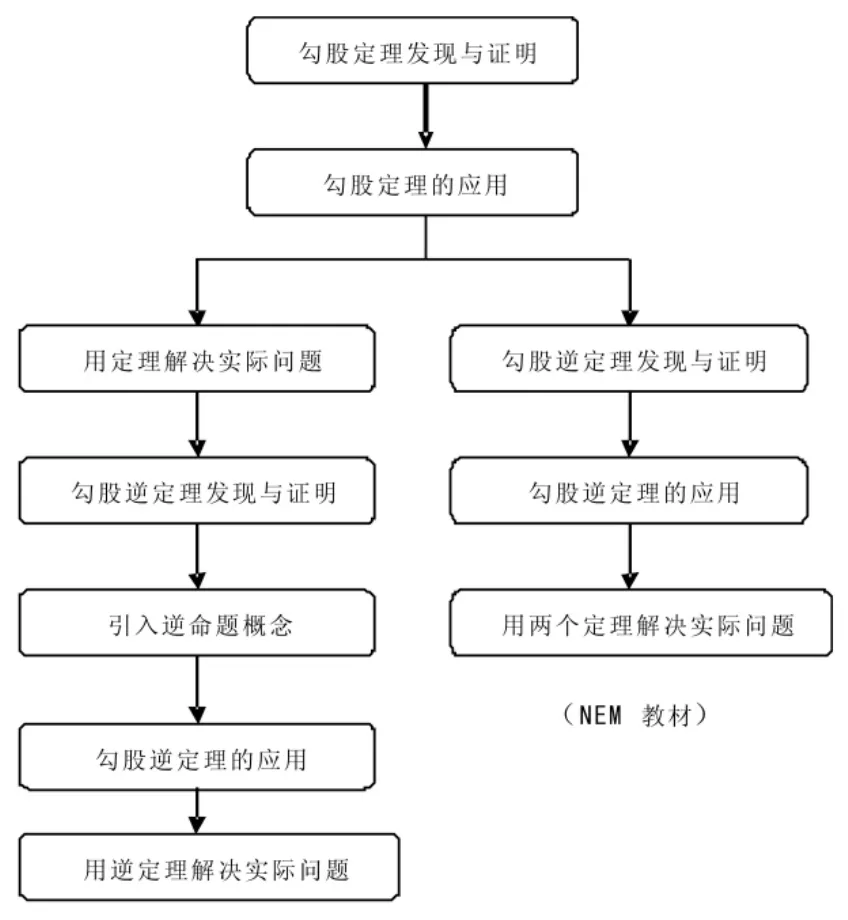
圖1 主要內(nèi)容與順序統(tǒng)計(jì)

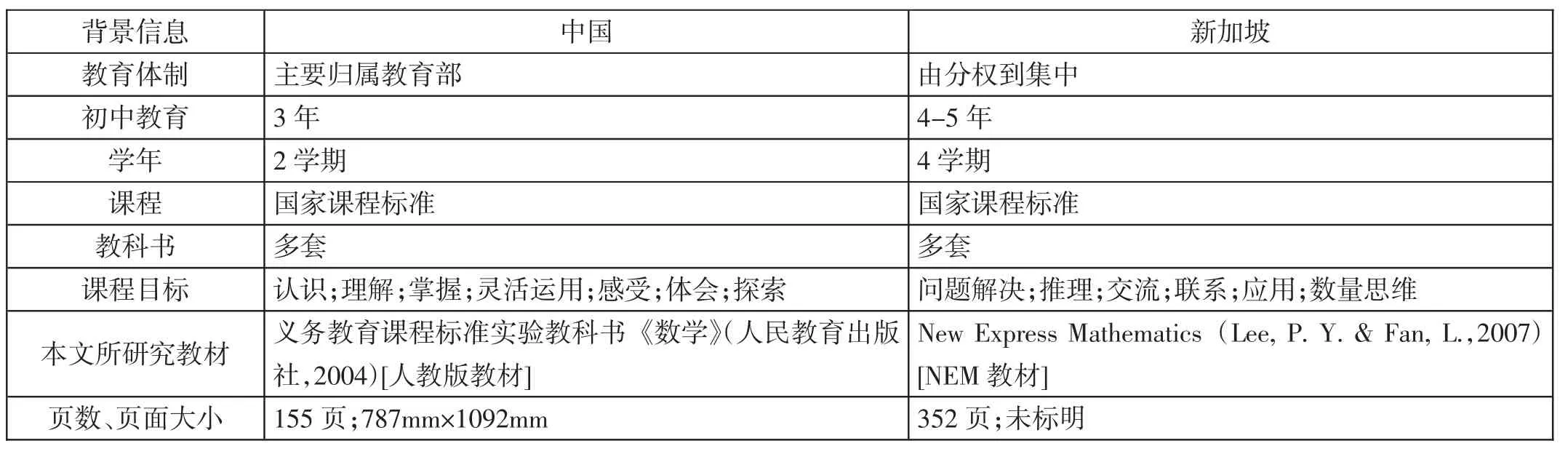
表3 背景信息統(tǒng)計(jì)

2.縱向維度指標(biāo)的度量

說(shuō)明：對(duì)于縱向維度中的其余各部分的統(tǒng)計(jì)結(jié)果，將在下文“研究結(jié)果”部分直接給出，此處不再以表格形式呈現(xiàn)。

三、研究結(jié)果

（一）教材呈現(xiàn)方式

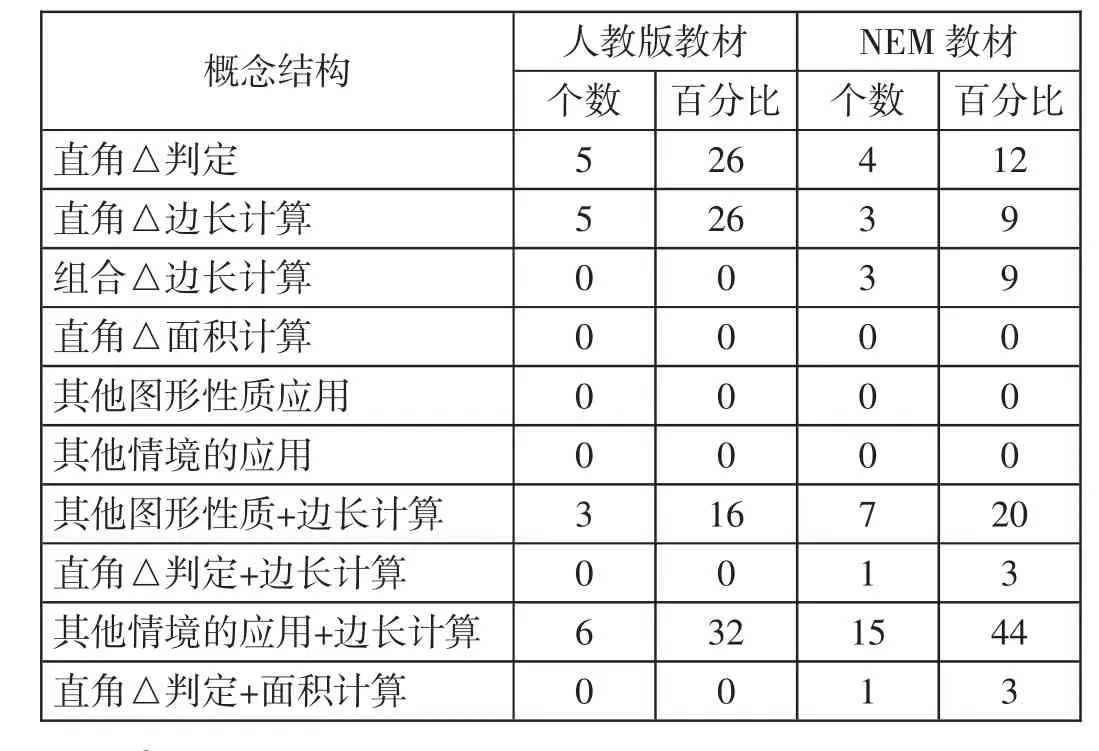
表4 不同概念結(jié)構(gòu)（針對(duì)任務(wù)）統(tǒng)計(jì)

通過(guò)比較教材主要內(nèi)容與順序（見(jiàn)圖表1），能夠發(fā)現(xiàn)兩本教材在內(nèi)容選擇上基本一致，但是在順序編排上有所差異。人教版教材在證明了勾股定理之后，所設(shè)置的課后習(xí)題大部分為實(shí)際應(yīng)用問(wèn)題，解題難度較大。而在NEM教材中，7.2小節(jié)“勾股定理”與7.3小節(jié)“勾股逆定理”的課后習(xí)題都是簡(jiǎn)單、直觀的邊長(zhǎng)計(jì)算。“用勾股定理解決實(shí)際問(wèn)題”被單獨(dú)列為本章的最后一個(gè)小節(jié)。作者認(rèn)為NEM教材的編排順序更為合理。

（二）教材對(duì)學(xué)生的期望

在NEM教材中，涉及數(shù)形結(jié)合思想、方程思想、轉(zhuǎn)化思想等數(shù)學(xué)思想的任務(wù)占總數(shù)的百分比為82%，人教版教材為68%。如此高的比例可見(jiàn)培養(yǎng)學(xué)生數(shù)學(xué)思維在初中階段越來(lái)越被重視。從認(rèn)知要求的角度來(lái)看，兩本教材都屬于高認(rèn)知要求。教材中的低水平任務(wù)（即記憶型任務(wù)）所占的百分比較低（NEM教材15%，人教版教材11%）。兩本教材中都只有21%的任務(wù)只要求學(xué)生給出一個(gè)答案，其余都需要進(jìn)行數(shù)學(xué)陳述。另外，人教版教材還引入了“逆命題”這一概念，并在任務(wù)中包含了部分需要推理論證的題目，對(duì)學(xué)生提出了更高的要求。基于以上比較結(jié)果，作者認(rèn)為人教版教材對(duì)學(xué)生的期望要略高于NEM教材。

四、啟示

（一）“高期望”是否等于“高質(zhì)量”

在上面文中作者得出了“人教版教材對(duì)學(xué)生的期望更高”的結(jié)論，但事實(shí)上在教學(xué)評(píng)估中新加坡的教學(xué)質(zhì)量總是高于中國(guó)，可見(jiàn)教材對(duì)學(xué)生的要求高并不一定能使得學(xué)生的知識(shí)水平高。中國(guó)學(xué)生的自主探究能力還不能達(dá)到教材要求的水平，這使得更多的時(shí)候需要教師去引導(dǎo)學(xué)生完成探究，學(xué)生的主體性反而減弱。

（二）教材所傳遞的新理念

兩本教材都淡化了勾股定理的證明，增加了實(shí)際應(yīng)用問(wèn)題的數(shù)量。這一特點(diǎn)向我們傳達(dá)一個(gè)訊息：如何將所學(xué)知識(shí)更好地運(yùn)用于生活，提高學(xué)生的實(shí)際應(yīng)用能力在數(shù)學(xué)教學(xué)中越來(lái)越受到關(guān)注。另外，NEM教材在本章節(jié)中多次使用了圖形軟件來(lái)進(jìn)行教學(xué)。將信息技術(shù)與數(shù)學(xué)課程進(jìn)行整合可以說(shuō)是數(shù)學(xué)教育發(fā)展的必然趨勢(shì)，但是在中國(guó)的教科書(shū)中還不常見(jiàn)。

（三）對(duì)所用研究框架的評(píng)價(jià)

Charalambos Y.Charalambous等在建立研究框架時(shí)設(shè)置了縱橫兩個(gè)維度，很好地彌補(bǔ)了之前單一維度框架的缺陷，既能研究教材細(xì)節(jié)又能從總體上把握教材內(nèi)容，并能夠研究不同教材對(duì)學(xué)生的不同期望，在教材比較中值得被借鑒。但也存在一些缺陷，如在縱向維度中所包括的“學(xué)生的態(tài)度”、“教材與課堂之間的聯(lián)系”等指標(biāo)。因此，作者認(rèn)為該研究框架的縱向維度上可以再設(shè)計(jì)一些理論性的指標(biāo)。

[1]張維忠,李芳奇.新加坡與中國(guó)數(shù)學(xué)教材的特色比較[J].外國(guó)中小學(xué)教育,2009，(02):32-36

[2]Charalambos Y.Charalambous,Sean Delaney,Hui-Yu Hsu and Vilma Mesa.A Comparative Analysis of the Addition and Subtraction of Fractions in Textbooks from Three Countries[J].Mathematical Thinking and Learning,2010,(12):117-151

[3]義務(wù)教育課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書(shū)[M].北京：人民教育出版社，2008

[4]Lee,P.Y.&Fan,L.(Eds.)New Express Mathematics.Singapore,Multimedia Communications Press,2007

[5][6]袁思情，陳月蘭.一篇值得推薦的數(shù)學(xué)教材分析框架文章[J].數(shù)學(xué)教學(xué)，2011，（04）：21-24