基于切趾濾波的線性調頻步進信號柵瓣抑制方法

仲利華 韓 冰 胡東輝 丁赤飚

①(中國科學院空間信息處理與應用系統技術重點實驗室 北京 100190)

②(中國科學院電子學研究所 北京 100190)

③(中國科學院研究生院 北京 100039)

1 引言

在SAR, ISAR成像中，為了獲得高分辨率距離像，需要發射大帶寬信號，如線性調頻信號。然而，當發射信號的瞬時帶寬太大時，系統成本和系統復雜度大大增加，同時受到硬件性能的制約，系統幅相誤差變大，信號質量下降，難以滿足高分辨率成像的要求。線性調頻步進信號(Frequency-Stepped Chirp Signal, FSCS)[1]是指連續發射一組經不同載頻調制的子脈沖，子脈沖為帶寬較小的線性調頻信號。對子脈沖回波采用頻譜合成的方法等效獲得大帶寬信號，大大降低了系統的瞬時帶寬，成為獲得高分辨率距離像的有效手段，并廣泛應用于高分辨率SAR, ISAR成像[2-5]。

通常，在系統設計時，線性調頻步進信號的相鄰子脈沖頻譜之間會有一定的冗余，這將導致脈沖壓縮結果中出現較強的柵瓣。強目標的柵瓣不僅會引起虛假目標的出現，還會導致弱小目標被淹沒。針對線性調頻步進信號柵瓣抑制的研究由來已久，文獻[6]分析了子脈沖帶寬，時寬和頻率步進長度等因素對柵瓣的影響，提出通過信號參數選擇使柵瓣位于脈沖壓縮后信號零點處以抑制柵瓣，該方法需要對信號參數進行復雜的設計優化，并且通常只能抑制部分柵瓣，仍然會有較強的殘余。文獻[7]通過改變子脈沖的脈沖寬度，破壞子脈沖間的周期性來實現柵瓣抑制，文獻[8]提出了非線性調頻步進信號的設計方法，避免了柵瓣的出現，但都增加了系統的復雜度。文獻[9]提出對子脈沖信號和合成后的全脈沖信號分別加權以抑制旁瓣和柵瓣的方法，但會導致系統分辨率下降。在文獻[9]的基礎上，文獻[10]提出對子脈沖加權后對全脈沖信號進行 SVA(Spatially Variant Apodization)處理的算法，在不損失分辨率的條件下降低了系統旁瓣和柵瓣，但該方法對信號參數敏感，針對不同的信號參數，抑制效果起伏較大。

本文在文獻[10]的基礎上通過詳細分析線性調頻步進信號自相關函數的組成和特點，提出對子脈沖采用不同窗函數加權后，對全脈沖壓縮結果進行切趾濾波來抑制柵瓣的方法，并給出了一種基于圖像域的快速計算方法。對柵瓣抑制后信號再次采用SVA算法，即可同時實現旁瓣抑制。理論分析和仿真實驗表明，針對子脈沖帶寬大于調頻步進長度的信號，該方法在不損失分辨率的條件下可以有效抑制旁瓣和柵瓣，且對信號參數不敏感，針對不同的信號參數均可獲得穩定的抑制效果。

全文結構如下，第2節對線性調頻步進信號自相關函數的構成和特點進行了詳細分析；第3節在回顧切趾濾波算法的基礎上，提出了一種子脈沖加權后對全脈沖信號進行切趾濾波的柵瓣抑制方法，并給出了其在圖像域的快速實現方法；第4節通過仿真實驗和真實數據處理驗證了算法的有效性；第5節為結束語。

2 線性調頻步進信號柵瓣分析

假設一個線性調頻步進信號由N個子脈沖組成，子脈沖帶寬為BwMHz，脈沖寬度和脈沖重復周期分別為Tp和Tr，子脈沖之間頻率步進長度為ΔFMHz，則該線性調頻步進信號表示形式如式(1)所示。

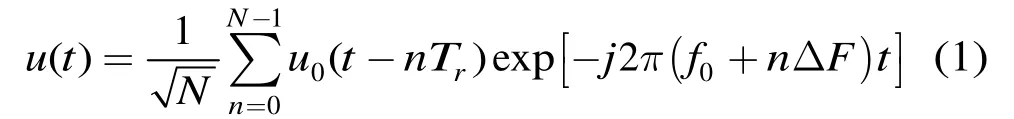
文獻[10]對線性調頻步進信號的性質做了詳細分析，對于式(1)中的信號，其自相關函數如式(2)所示。

3 基于切趾濾波的柵瓣抑制算法

3.1 切趾濾波柵瓣抑制原理

切趾濾波來源于光學信號處理，并被廣泛應用于SAR, ISAR旁瓣抑制中[11]。其基本原理是通過對信號采用不同的頻域窗函數進行加權后，逐點判斷不同加權結果的符號是否改變來區分主瓣和旁瓣。然而直接將 DA, SVA等切趾濾波方法應用于線性調頻步進信號并不能實現柵瓣抑制。受到子脈沖頻率周期性步進的影響，柵瓣位置處符號在采用不同窗函數加權后并沒有改變，導致DA或SVA的判斷標準失效，柵瓣被誤認為主瓣而被保留。

通過第2節中對線性調頻步進信號自相關函數和切趾濾波算法的分析研究[11]，本節給出一種基于子脈沖加權的切趾濾波方法，以實現對線性調頻步進信號柵瓣的抑制。其基本原理如圖1所示。

圖1 子脈沖加權切趾濾波示意圖

當調頻步進頻率ΔF小于子脈沖信號帶寬Bw的時，第1柵瓣出現時刻1/ΔF大于子脈沖第1零點1/Bw，因此，所有柵瓣均位于子脈沖自相關函數主瓣之外。由文獻[11]可知，對線性調頻信號進行適當的頻域加權可以改變其自相關函數主瓣之外信號的符號。結合式(2)，通過對子脈沖進行加權，改變s1(τ)主瓣外符號，而s2(τ)保持不變，即可改變s(τ)中子脈沖主瓣之外信號的符號，由于所有柵瓣均位于子脈沖主瓣之外，所以可以通過切趾濾波實現對所有柵瓣的抑制。此時，s(τ)中仍然存在位于子脈沖主瓣內的旁瓣，再次對s(τ)采用SVA進行處理后即實現對剩余旁瓣的抑制。總結上述分析可以確定基于切趾濾波的柵瓣、旁瓣抑制方法處理流程如圖2所示。

圖2 基于切趾濾波的柵瓣旁瓣抑制算法框圖

3.2 基于圖像域的快速實現算法

3.1節中的處理流程需要獲得信號在不加權、子脈沖加權、全脈沖加權3種形式下的脈沖壓縮結果，增加了處理的計算量，本節將基于傳統的SVA算法推導本文方法在圖像域的快速實現算法。

采用余弦底座窗函數作為子脈沖頻域加權函數，其形式如式(3)所示。

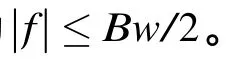
線性調頻步進信號由N個子脈沖構成，將W0(f)在頻域進行平移構成對第k個脈沖的加權函數為

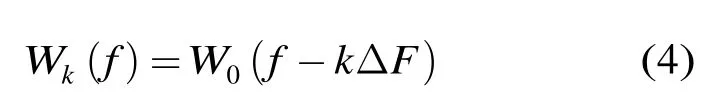
然而受到相鄰頻譜重疊的影響，總的加權函數并不等于各個子脈沖加權函數的疊加，而是隨子脈沖帶寬Bw和頻率步進長度ΔF的影響而變化。通常，Bw的選擇不會遠大于ΔF，因此只對1＜Bw/ΔF＜ 3 的情況進行討論。當1＜Bw/ΔF≤2 時，修正的子脈沖窗函數形式如式(5)所示。

修正后的窗函數脈沖響應為

其中，ωs1=Fs/ΔF,ωs2=Fs/(Bw)。則W(f)的時域脈沖響應為

將上述窗函數作用于未加窗的脈沖壓縮結果g(m)得

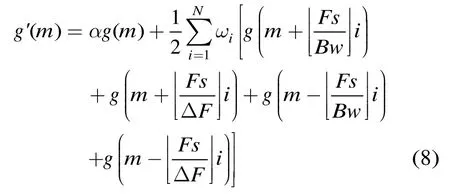
當2＜Bw/Δf＜ 3 時，可以采用類似的分析方法獲得最終結果，由于篇幅所限，這里不再給出具體推導過程。

通過選取合適的ωi可以使得g'(m)最小化。然而在不加任何約束的情況下，最小化的g'(m)為零，因此，參考SVA，對a和ωi做出如下限制：

令N=1，式(8)可簡化為

上述問題是一個約束優化問題，不等式(9)表示的直線構成一個多邊形，極值在多邊形的頂點處取得。計算各個頂點處g'(m)的取值，如果某兩個頂點處g'(m)值符號相反，則給g'(m)賦零；否則取絕對值最小的那個作為g'(m)的取值。

下面就本文方法計算量展開分析。設圖像距離向大小為M，則采用3.1節中頻域加權處理方法的運算量和3.2節中快速方法運算量如表1所示。

表1 計算量對比

通常SAR圖像距離向大小約為8192～32768，因此根據表1計算可得，本文算法計算量僅為直接頻域加權處理算法的1/4～1/5，因此可以有效提高計算速度。

4 仿真試驗

4.1 單點目標仿真實驗及性能分析

本節將通過數值仿真實驗來對算法性能進行驗證。仿真參數的選取與文獻[10]保持一致，即線性調頻步進信號由11個子脈沖組成，子脈沖信號帶寬為80 MHz，脈寬為12 μs，子脈沖間頻率步進為34.5 MHz，發射時間間隔為15 μs。則合成頻譜帶寬為425 MHz，對應的距離分辨率為0.34 m。

圖3(a)給出了點目標匹配濾波結果，由于頻譜重疊的存在，1維距離像中存在較強的柵瓣，其中第1柵瓣強度達到-18.6 dB，這將會對弱目標的檢測與識別造成影響。

采用全脈沖加權和全脈沖SVA算法處理后旁瓣得到有效抑制，而柵瓣仍保持不變，其結果如圖3(a)所示。圖3(b)給出了采用子脈沖加權，子脈沖加權結合全脈沖SVA的處理結果，可以發現，柵瓣得到有效抑制，但第1柵瓣仍然較強，約為-30 dB。圖3(c)給出了本文方法處理結果，柵瓣和旁瓣均得到有效抑制。在理想情況下，本文對旁瓣和柵瓣的抑制相對于文獻[10]提高了接近30 dB。

圖3中各種算法柵瓣及旁瓣抑制效果如表2所示。通過圖3的對比分析發現，對子脈沖進行加權的處理方法可以一定程度上實現柵瓣抑制，但最靠近主瓣的若干個柵瓣，尤其是第1柵瓣無法有效抑制。由圖1可知，第1柵瓣位于子脈沖主瓣之外，當柵瓣出現位置正好位于子脈沖旁瓣的峰值附近時，將會導致柵瓣幅度較強，而當柵瓣出現位置比較接近子脈沖自相關函數過零點時，柵瓣較弱。柵瓣的強弱和子脈沖旁瓣、過零點之間的關系主要由子脈沖帶寬和子脈沖間步進頻長決定。因此，在傳統的柵瓣抑制方法中，子脈沖帶寬Bw和步進頻長ΔF之間的相對大小將會影響柵瓣抑制效果。在上述其它仿真條件不變的情況下，改變子脈沖信號帶寬，以驗證Bw/ΔF對不同方法的影響。

根據表2的對比，這里只對匹配濾波結果，子脈沖加權結合全脈沖SVA處理結果和本文方法處理結果進行對比分析。其中，匹配濾波結果作為參考用以衡量抑制效果。圖4給出了子脈沖帶寬與步進頻率不同比值情況下柵瓣抑制性能，可以看出，傳統的子脈沖加權類方法對信號參數較為敏感，當Bw/ΔF改變時，性能變化較大，而根據理論推導，由于所有柵瓣均位于主瓣外，所以采用本文方法在Bw/ΔF＞1 的條件下均可以得到較為穩定的結果。

4.2 多目標仿真實驗

對柵瓣、旁瓣進行抑制的目的是為了消除強目標副瓣對弱小目標的遮掩，提高識別能力。為此，本節將通過設置一強一弱兩個目標對本文算法性能進行仿真驗證。

圖3 柵瓣抑制效果仿真

表2 不同算法性能對比

圖4 頻率步進為34.5 MHz時不同子脈沖帶寬下各種算法柵瓣抑制性能對比

仍然采用上一節的仿真參數，實驗中假設存在兩個點目標，其中點目標1位于坐標原點，幅度為100，點目標2與點目標1的距離為5 m，幅度為1，即點目標2位于點目標1第1柵瓣附近，且幅度相對于點目標1弱40 dB。

圖5給出了匹配濾波結果、文獻[10]抑制結果和本文方法抑制結果的對比。從圖中看出，點目標 1第1柵瓣強度為-18.6 dB，經傳統方法抑制后降至-31 dB，但仍然強于目標2。這時目標2被目標1第1柵瓣遮掩，無法有效識別。而通過本文方法，目標1的柵瓣被降至-60 dB以下，目標2清晰可見。

4.3 分布場景目標仿真實驗

圖5 多點目標仿真

由于條件限制，尚未獲得真實的線性調頻步進體制下SAR/ISAR圖像，本文通過對一幅SAR數據進行處理，獲得等效線性調頻步進信號 SAR圖像。將一幅SAR數據在距離頻域分割為幾個子帶，每個子帶頻譜等效為子脈沖頻譜，相鄰子帶間存在一定的冗余，將各個子帶頻譜拼接等效形成大帶寬線性調頻步進信號。

原始 SAR信號參數和等效線性調頻步進信號參數如表3所示。通過仿真計算，在該組參數下，等效調頻步進信號在脈沖壓縮后第 1柵瓣強度為-14 dB，將會對圖像質量產生較大的影響。

表3 分布場景目標仿真實驗參數

圖6(a)和圖6(b)分別為原始SAR圖像和等效獲得的線性調頻步進信號SAR圖像。圖6(c)和圖6(d)分別為子脈沖加窗全脈沖SVA方法和本文方法處理結果。

從圖6(b)中可以看出，相對于原始SAR圖像，等效線性調頻步進信號圖像清晰度明顯下降，由于柵瓣的影響，強散射點附近出現了周期性的虛假峰值。

圖 6(c)為采用文獻[10]中的子脈沖加權結合全脈沖SVA方法處理結果，可以看出，部分柵瓣被消除，但仍有剩余。圖6(d)為采用本文方法處理結果，圖像質量大大提高，柵瓣抑制效果明顯。

通常采用圖像對比度[12]對 SAR 圖像質量進行評價，對比度定義如式(11)所示。

圖6 分布場景目標仿真實驗結果

其中C為圖像對比度，I(m,n)表示第(m,n)個像素的強度，E(·)表示圖像強度的均值。分別計算各種方法處理結果的對比度并進行比較，其結果如表 4所示。

表4 不同處理方法下圖像對比度

經過視覺觀測和定量化對比可知，本文方法較好地抑制了柵瓣的影響，圖像對比度相對于子脈沖加權結合全脈沖SVA算法提高了約13%，圖像整體質量得到改進。

5 結束語

針對線性調頻步進信號由于子脈沖間頻譜重疊導致的柵瓣，本文提出了一種基于子脈沖加權后采用切趾濾波進行柵瓣抑制的方法，并給出了其在圖像域的一種快速實現方法。仿真實驗表明，本文方法對柵瓣的抑制效果優于傳統方法。此外，本文3.1節提出的基本方法同樣適用于非線性調頻步進信號，而 3.2節的快速算法由于隱含了子脈沖之間線性步進的條件，對于非線性步進的情況將不再適用。

然而，本文方法只適用于頻譜間存在重疊的線性調頻步進信號，當步進頻率大于子脈沖帶寬，頻譜間存在間隙時，會造成部分柵瓣落于子脈沖主瓣內，根據本文方法該部分柵瓣無法得到抑制。未來工作將重點擴展算法的適用性，使其也適用于頻譜間不存在重疊的線性調頻步進信號。

[1]Levanon N. Stepped-frequency pulse-train radar signal[J].IEE Proceedings-Radar,Sonar and Navigation, 2002, 149(6):297-309.

[2]Liu Y, Xing M, Zhang L,et al.. Novel range profile synthesis algorithm for linearly stepped-frequency modulated inversed synthetic aperture radar imaging of remote maneuvering target[J].IET Radar,Sonar&Navigation, 2011, 5(4):496-506.

[3]Zhu Feng, Zhang Qun, Lei Qiang,et al.. Reconstruction of moving target’s HRRP using sparse frequency-stepped Chirp signal[J].IEEE Sensors Journal, 2011, 11(10): 2327-2334.

[4]何勁, 羅迎, 張群, 等. 隨機線性調頻步進雷達波形設計及成像算法研究[J]. 電子與信息學報, 2011, 33(9): 2068-2075.

He Jin, Luo Ying, Zhang Qun,et al.. Waveform design and imaging algorithm research of random frequency stepped Chirp signal ISAR[J].Journal of Electronics&Information Technology, 2011, 33(9): 2068-2075.

[5]Wang Hong-xian, Liang Yi, Xing Meng-dao,et al.. ISAR imaging via sparse frequency-stepped chirp signal[J].SCIENCE CHINA Information Sciences, 2012, 55(4):877-888.

[6]Nadav L and Mozeson E. Nullifying ACF grating lobes in stepped-frequency train of LFM pulses[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(2): 694-703.

[7]Gladkova I and Chebanov D. Grating lobes suppression in stepped-frequency pulse train[J].IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1265-1275.

[8]Gladkova I and Chebanov D. Suppression of grating lobes in stepped-frequency train[C]. Proceedings of IEEE International Radar Conference, Arlington, Va, USA, May 2005: 371-376.

[9]Li Hai-bin, Zhang Yun-hua, and Wu Jie. Sidelobes and grating lobes reduction of stepped-frequency Chirp signal[C].IEEE International Symposium on Microwave, Antenna,Propagation and EMC Technologies for Wireless Communications Proceedings, Beijing, China, August 2005:1210-1213.

[10]李海濱. 調頻步進信號及逆合成孔徑雷達成像方法研究[D].[碩士論文], 中國科學院空間科學與應用研究中心, 2005.

[11]倪崇, 王巖飛, 徐向輝, 等. 一種基于改進SVA的SAR旁瓣抑制算法[J]. 中國科學: 技術科學, 2010, 40(12): 1485-1494.

Ni C, Wang Y F, Xu X H,et al.. A SAR sidelobe suppression algorithm based on modified spatially variant apodization[J].SCIENCE CHINA Technological Sciences, 2010, 53(10):2542-2551.

[12]Berizzi F and Corsini G. Autofocusing of inverse synthetic aperture radar images using contrast optimization[J].IEEE Transactions on Aerospace and Electronic Systems, 1996,32(3): 1185-1191.