一種基于WSN時變性與節點剩余能量均衡的機會路由算法

丁 男 譚國真 由 笛 張 偉

(大連理工大學計算機科學與技術學院 大連 116023)

1 引言

無線傳感器網絡(Wireless Sensor Network,WSN)，與移動Ad hoc網絡和無線MESH網絡一樣，在很多重要領域被認為是一種方便的、經濟的解決方案，比如交通監控、環境監測、軍事安全等。

在實際應用中，多數用于 WSN的多跳路由算法是從有線網絡中演變過來的。因此，在此類路由算法的設計過程中，往往需要假設 WSN是一個拓撲已知的網絡，其通信鏈路是靜態的、不變的。數據報文在利用該類路由算法進行傳輸過程時，是基于已建立好的路經進行傳輸的，沒有考慮網絡拓撲及各節點狀態的動態變化[1,2]。

機會路由是近幾年所提出的一種新的基于多跳的動態路由。文獻[3]根據無線信道的衰減和干擾特性，認為WSN 中節點正確接收的數據報文服從一定的概率分布，并提出一種基于機會的傳輸方式，即當無線信道的條件合適時，無線節點才進行通信。機會路由機制可以提高數據報文在無線通信網絡中傳輸性能，但是動態建立路徑也給機會路由算法在設計上帶來了難題[4]。

目前已有的工作主要集中在兩方面研究。一方面是集中在為數據報文在傳輸過程中尋找基于WSN時變特性下的最短路徑的策略與相應路由算法研究。文獻[5]通過結合圖論和網絡流理論，針對最大網絡流最短路徑問題為機會路由的吞吐率建立了優化模型，為機會路由動態建立傳輸路徑的相關研究提供了理論依據。文獻[6]將數據包傳輸過程模仿蜜蜂采蜜的過程，設計了一個 RSSI(Received Signal Strength Indicator)機會路由算法，根據傳輸中各節點的信號強度動態調整節點的機會選擇概率，以機會概率值選擇報文所能到達的最佳節點進行數據轉發。文獻[7]引入蟻群優化算法，將 WSN中數據傳輸路徑的動態選擇，模擬螞蟻覓食過程中在路徑上殘留的信息素誘導后面的螞蟻盡快地找到到達目的地的過程。另一方面是以考慮網絡中節點能耗問題為核心的動態路徑建立策略及相應機會路由算法研究。文獻[8]提出了兩種考慮能耗的適用于機會傳輸的傳輸策略，一種是利用閾值判斷的方法在動態建立傳輸路徑時，排除網絡中剩余能量少的節點，該策略適用于所有機會傳輸方式，另一種策略是針對無線傳感器網絡傳輸具有中心性的特點，將網絡中節點以接收節點為中心，分成同心環型層次，在考慮剩余能量的基礎上，使得各節點能量消耗分配更合理。文獻[9]結合基于已建立傳輸路徑整體的剩余能量問題，利用蟻群優化算法提出了一個EEABR(Energy Efficient Ant Based Routing)的路由算法。

分析上述研究，機會路由在動態建立路徑過程中，網絡傳輸的最短路徑問題與網絡節點剩余能量的均衡問題既相互影響，又相互制約。一些學者雖然考慮這兩方面的關系，提出一些機會路由算法，主要是在考慮節點能耗的同時利用蟻群優化等啟發式算法給出傳輸路徑選擇策略[10,11]。目前，缺少針對時變特性的網絡路徑優化與節點剩余能量均衡問題協同考慮的理論模型與分析方法。因為在考慮網絡時變特性，傳統靜態網絡相關理論是失效的[12,13]。

針對上述問題，本文結合熱力學第2定律，在考慮網絡中節點剩余能量以及在選擇數據報文最優傳輸路徑的時變性等因素前提下，對 WSN數據傳輸過程進行理論分析與描述，提出了機會熵模型，并以此為依據，結合蟻群優化(ACO)算法，提出了一個新的路由算法 ATDOP(ACO for Time Dependent Opportunistic-routing Protocol)。

2 網絡模型與問題分析

2.1 網絡模型

本文假設網絡中各節點隨機分布在一個矩形區域內，并且具有如下性質：(1)網絡內Sink節點惟一，部署在網絡中央位置，其余傳感器節點部署后不再移動，并且各節點的地理位置信息不可知；(2)每個節點有惟一的標識；(3)所有節點平等，具有相同的計算、通信能力以及初始能量。

結合上面假設，給出網絡模型的如下定義：

定義2通信距離。在圖G中，通信距離，記為hu，表示節點u與Sink節點之間的通信跳數，用以表示距離Sink節點的距離。

定義3網絡壽命。本文將從 WSN開始工作直到網絡內第1個節點死去時，Sink節點所接收到的所有數據報文，其各自傳輸過程中到達Sink節點的跳數累計之和，定義為網絡壽命。

定義 4節點o的鄰居集，記為N(o)=ui(ui∈U,eoui∈E)，表示與節點o直接通信的節點ui集合。

2.2 時間依賴的最短路徑

在圖G中，任意節點o與Sink節點s之間路徑(o,u1,…,ui,…,s)，為了能夠讓數據報文沿著向Sink節點接近的方向快速傳遞，根據文獻[3]所提出的機會概率模型，在考慮網絡的時變特性，我們提出了一個在節點o的鄰居節點中選擇下一跳節點方法。

式中hu代表u節點距離s節點的距離。wu(t)表示在t時刻，節點o與其鄰居集合N(o)中節點u的通信權重，其值在實驗中可根據隨機概率模型獲得，例如文獻[4]，在實際應用中，可以通過測量信號強度獲得。

為了便于描述與分析該問題，結合網絡中基于時間依賴的最短路徑的研究[13]，本文對機會路由的最短傳輸路徑進行如下規劃：

其中D(o,s,t)表示，在t時刻下，由源點o到目的點s的傳輸路徑。

定理1在無線傳感器網絡中，采用機會傳輸方式的WSN是一個no-FIFO的網絡。

證明假設該 WSN拓撲圖G(V,E)，如圖 1所示。其中V={o,u1,u2,u3,u4,u5,u6,u7,s},E={e(o,u1),e(u1,u2),e(u1,u3),e(u2,u3),e(u2,u4),e(u3,u4),e(u3,u5),e(u4,u6),e(u5,u7),e(u6,s),e(u7,s)}各節點從接收報文或產生報文，到將該數據轉發給下一跳節點需要Δt時間。假設在t1時刻，由o節點發送一數據報文M1，在t1+Δt時刻，o節點發送M2。當M1達到u1時，u1選擇u2作為M1的下一跳。當M1到達u2時，由于能量消耗等問題，u1,u2之間的通信權重發生變化，u1在轉發M2時選擇u3作為下一跳節點。而當M1到達u4時，u6節點由于網絡擁塞或者故障等原因，u4選擇u3作為下一跳節點，這樣在t1+4Δt時，M1到達u3，而M2到達u5。最終，M2比M1早到s節點。M1經過的路徑為Pa(M1)={o,u1,u2,u4,u3,u5,u7,s}，用時7Δt；而M2經過的路徑為Pa(M2)={o,u1,u3,u5,u7,s} ，用時5Δt。因此，在考慮通信連路的時間依賴特性，采用機會傳輸方式的無線傳感器網絡的鏈路傳輸是no-FIFO的。 證畢

圖1 網絡通信圖案例

定理2采用機會傳輸方式的WSN，其基于時間依賴特性的最短路徑問題是一個NP難解問題。

證明根據定理 1，基于機會路由通信機制的WSN網絡，其網絡通信具有no-FIFO特性。 而文獻[12]已證明，在時變網絡中如果通信連路是 no-FIFO，其最短路徑算法的復雜度是NP的。因此，在機會路由中，基于時變的最短路徑問題是一個NP難解問題。 證畢

2.3 能量問題

(1)能量消耗矩陣 根據文獻[14]無線傳感器節點存在3個工作狀態：空閑、發送和接收，我們建立能量消耗矩陣E為

其中各元素Eij，當i≠j，表示狀態i轉變成狀態j所需消耗的能量，當i=j，表示節點在持續狀態i時所消耗的能量。

(2)基于時間依賴的能量預測模型 根據上述能量消耗的能量矩陣，建立節點剩余能量的最優估計值Eop(t)：

其中El(t)表示當前節點剩余能量，可由節點實時獲得；Es(t)表示t時刻，在i狀態下，節點在T時間內能源消耗的預測值，其值基于能量消耗可能量矩陣E，根據式(6)計算而得，其中，T=2。

2.4 機會熵

1850年，德國物理學家魯道夫·克勞修斯提出：在一個獨立的系統中，能量密度的差異傾向于變成均等。這也是熱力學第2定律的核心思想。并且定義熵(S)表示系統在不受外部干擾的情況下，系統通常往內部最穩定狀態發展的特性。1872年，波爾茲曼進一步從分子運動的角度對克勞修斯的熱力學熵理論進行了發展，進一步解釋了系統由不穩定到穩定過程中，各分子的能量衰減過程，并提出了微觀態的概念[15]，從微觀的角度體現了一個物質系統中各分子能量的衰竭程度。通過比較各分子的熵值大小，就可以辨別出系統的轉化方向，即往S值大的趨勢發展。

這個現象可以用于描述數據報文在 WSN傳輸過程中，各節點狀態以及剩余能量的變化趨勢。根據熱力學第2定律，將整個WSN看作是一個獨立的、密閉的系統，我們通過定義機會熵，來描述每個WSN節點的狀態。

定義5機會熵(opportunistic entropy)用Sop表示，它表征節點在自身能量有限并且能量不可再生的前提下，其自身狀態的活躍程度，表示為

其中，剩余能量的最優估計值Eop(t)，由式(5)可得。wu(t)同式(3)。

3 基于蟻群算法的機會路由算法ATDOP

3.1 基于Sop的機會概率模型

根據傳統蟻群優化算法中用信息素作為節點被選概率模型的思想[7]，結合機會熵Sop，本文提出了一個新的概率計算公式。

其中N(u)為u節點的鄰居集，ui和uj分別為u節點鄰居集中的節點；P(uj,t)為在第t時刻，螞蟻將報文從節點u傳遞到下一節點uj的概率，即當前節點選擇節點uj作為下一跳的概率；τ(uj,t)為在第t時刻下，節點uj上的信息素濃度；Sop(uj,t)為在第t時刻下，節點uj的機會熵；β為系統參數，它用來調整Sop(uj,t)對P(uj,t)中的影響程度，其值根據具體實驗環境由經驗設定，本文實驗中β=1。基于式(8)，在傳輸過程中，選擇P值最大的節點作為下一接收節點。

3.2 信息素更新

當節點u將數據報文發送給節點uj完畢之后，節點uj會自我更新信息素τ(uj,t)。由于信息素是決定螞蟻選擇路徑的關鍵因素之一。因此，本文在提出信息素計算模型時引入了殘留率ρ(t)。

其值與當前節點剩余能量相關，當節點能量剩余越少，ρ(t)值越小，意味著信息素的揮發越快。Einit表示節點初始能量值。通過根據能量調整殘留率ρ(t)，可以使剩余能量少的節點的信息素揮發速度快。

初始化時，網絡中各節點都被設置為相同的初始值；τ(uj,t-1)表示t-1時刻節點uj的信息素；Δτ(uj,t)表示第t時刻節點uj信息素的增加值，其值由式(11)可得

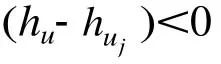
3.3 ATDOP算法

根據上述的信息素以及機會概率的計算模型，本文設計了基于蟻群優化算法的時間依賴機會路由協議算法(ATDOP)。其結構如圖2所示。

(1)初始化 該狀態下，由Sink節點通過泛洪的方式在網絡內發送初始化信息，主要對算法中所需的各節點距離Sink節點的最短跳數h，信息素更新時間Tw，鄰居節點集信息收集等待Tc，能量枯竭判斷閾值ε，螞蟻(數據報文)到達標志Fa,β, Δω等信息進行初值化。

圖2 ATDOP結構圖

(2)等待螞蟻 一方面等待自身節點是否產生新螞蟻要發送，如果有，則進行鄰居節點的狀態查詢。另一方面監聽網絡，如果有鄰居螞蟻達到，判斷該報文是否是查詢節點狀態，如果是，則返回自身節點狀態(ID，機會熵Sop，信息素信息τ(uj,t))，然后再次進入監聽狀態；如果是需要轉發的報文，則進行鄰居節點的狀態查詢，為報文轉發做準備。

(3)查詢鄰居節點狀態 該節點會向鄰居節點集N發送請求信息，在等待時間Tc內，收集鄰居節點返回的各自Sop和τ(uj,t)，并計算機會選擇概率P(uj,t)。

(4)選擇節點 選擇機會選擇概率P(uj,t)最大的節點，建立傳輸路徑，發送螞蟻。

(5)信息素更新 信息素的自我更新，該狀態主要有兩個進入源：其一是在發送螞蟻后立即自我更新，其二是在節點等待Tw時間后，進行自我更新(該處是對信息素的揮發處理)。

4 實驗仿真與性能分析

4.1 仿真環境的建立

本文利用 NS-2 實驗軟件進行相關實驗驗證。仿真參數如表1所示。

表1 實驗參數

4.2 性能分析與比較

本實驗環節將ATDOP算法與以下兩個路由算法進行比較：(1)基于傳統的蟻群算法的路由算法，BACO(Basic Ant Colony Optimization)，文獻[7,11]將傳統的蟻群算法用在求解近似最短路由；(2)EEABR(Energy Efficient Ant Based Routing)路由算法[9]，該算法同樣是基于蟻群算法，并參考了整體路徑的剩余能量，剩余能量多的，將具有高的被選擇機會。

在相同的仿真環境以及網絡拓撲規模，根據本文中對網絡壽命的定義，即當網絡內任意一節點的剩余能量低于枯竭判斷閾值ε時，實驗停止。實驗中，ε取能量初始值的10%。

(1)針對網絡壽命，采用 BACO, EEABR和ATDOP 3個路由算法，分別進行了100次實驗，結果如表2所示。

表2 平均網絡壽命

傳統的蟻群算法由于沒有考慮節點的能耗，使得信息素高的節點被頻繁選中傳輸信息，所以導致網絡壽命最短；EEABR路由算法參考了路徑中的節點的平均能量，并且在數據包到達Sink后再對整條路徑上的節點一起更新，但該路徑上個節點的剩余能量的沒有單獨考慮，雖然在網絡壽命上有很大提高，但是仍略低于本文的ATDOP算法。

(2)針對各節點剩余能量的分布情況，我們同樣統計了上述100次的實驗結果，如圖3所示，其中橫軸為能量剩余率，縱軸為占節點總數比例。

BACO路由算法，由于螞蟻在行進過程中沒有考慮能量，信息的傳輸主要集中在最初所建立的近似最優路徑上，能量的消耗也主要集中在這部分節點上，實驗停止時只有 30%的節點剩余能量低于35%。而EEABR與ATDOP算法由于考慮到剩余能量問題，實驗停止時大約70%以上的節點剩余能量低于能量初始值的35%。

(3)針對網絡吞吐率，本實驗將上述3個路由算法進行了100次的實驗比較，其吞吐率分析如圖4所示。

其縱軸為Sink節點接收到數據包，橫軸為網絡內各節點的累計跳數和，斜率即為該時刻所對應的吞吐率。3個路由算法在實驗初期，其吞吐率接近，但隨著實驗的進行，由于傳統蟻群算法沒有考慮能耗，所以該算法的吞吐率比較穩定，而EEBAR與ATDOP由于考慮了節點的剩余能量，因此在實驗后期，傳輸路徑會動態地調整，跳數增多，二者的吞吐率都有下降，但ATDOP由于同時考慮了最短路徑問題，因此其吞吐率好于EEBAR算法。

5 結論

本文在分析已有的機會路由算法的基礎上，利用熱力學第2定律對在時變特性下WSN網絡數據報文的傳輸過程進行分析與描述，并參考熱力學中熵的概念，以節點剩余能量和距離Sink節點的傳輸距離作為狀態變量，提出了機會熵模型，并用以表征 WSN中各節點的傳輸狀態。基于該模型，數據報文動態選擇傳輸路徑也就是選擇機會熵小的節點作為轉發節點。進而，本文將機會熵模型與蟻群優化算法相結合，提出了一個適用于時變網絡模型的考慮網絡資源負載均衡的機會路由算法(ATDOP)。最后，實驗仿真表明，該路由算法相對于已有的基于原始蟻群算法的機會路由算法以及考慮能量的EEBAR機會路由算法的網絡工作壽命更長，能量消耗的更均勻，網絡資源分配的更合理。

圖3 節點剩余能量的分布

圖4 吞吐率

[1]Abhijeet B, Mohammad N, Javidi T,et al.. Adaptive opportunistic routing for wireless ad hoc networks[J].IEEE/ACM Transactions on Networking, 2012, 20(1):243-256.

[2]熊永平, 孫利民, 牛建偉, 等. 機會網絡[J]. 軟件學報, 2009,20(1): 124-137.

Xiong Yong-ping, Sun Li-min, Niu Jian-wei,et al.. Opportunistic networks[J].Journal of Software, 2009, 20(1): 124-137.

[3]Sanjit B and Robert M. ExOR: opportunistic multi-hop routing for wireless networks[C]. Proceedings of ACM SIGCOMM, Pennsylvania, 2005: 133-143.

[4]Bo H, Pan H, and Kumar A. Mobile data offloading through opportunistic communications and social participation[J].IEEE Transactions on Mobile Computing, 2012, 11(5):821-834.

[5]Kai Z, Wenjing L, and Hongqiang Z. On end-to-end throughput of opportunistic routing in multirate and multihop wireless networks[C]. Proceedings of the IEEE INFOCOM, Phoenix, AZ, USA, 2008: 1490-1498.

[6]霍廣城, 王曉東. 移動傳感網中一種基于RSSI 的機會主義路由設計[J]. 電子學報, 2009, 37(3): 608-613.

Huo Guang-cheng and Wang Xiao-dong. An opportunistic routing for mobile wireless sensor networks based on RSSI[J].Acta Electronica Sinica, 2009, 37(3): 608-613.

[7]Paquereau L and Helvik E. Opportunistic ant-based path management for wireless mesh networks[C]. International Conference on Swarm Intelligence, Beijing, China, 2010:480-487.

[8]Lakshmi V, Kailas A, and Ingram A. Two energy-saving schemes for cooperative transmission with opportunistic large arrays[C]. Proceedings of IEEE GLOBECOM, Washington DC, USA, 2007: 1038-1042.

[9]Tiago C, Carlos C, Jorge S,et al.. An energy-efficient ant-based routing algorithm for wireless sensor networks[C].Ant Colony Optimization and Swarm Intelligence, 2006, 4150:49-59.

[10]宋超, 劉明, 龔海剛, 等. 基于蟻群優化解決傳感器網絡中的能量洞問題[J]. 軟件學報, 2009, 20(10): 2729-2743.

Song Chao, Liu Ming, Gong Hai-gang,et al.. ACO-based algorithm for solving energy hole problems in wireless sensor networks[J].Journal of Software, 2009, 20(10): 2729-2743.

[11]Lee W. Ant-colony-based scheduling algorithm for energyefficient coverage of WSN[J].IEEE Sensors Journal, 2012,12(10): 3036-3046.

[12]Ariel O and Rapheal R. Shortest-path and minimum-delay algorithms in networks with time-dependent edge-length[J].Journal of the ACM, 1990, 37(3): 607-625.

[13]譚國真, 高文. 時間依賴的網絡中最小時間路徑算法[J]. 計算機學報, 2002, 25(2): 165-172.

Tan Guo-zhen and Gao Wen. Shortest path algorithm in time-dependent networks[J].Chinese Journal on Computers,2002, 25(2): 165-172.

[14]Al-Jarrah O and Megdadi O. Enhanced AODV routing protocol for bluetooth scatternet[J].Computers and Electrical Engineering, 2009, 35(1): 197-208.

[15]Pincus S M. Approximate entropy as a measure of system complexity[J].Proceedings of the National Academy of Sciences of the United States America, 1991, 88(6):2297-2301.