多維不確定性XML數據模型的研究

王 艷，樂嘉錦，姜久雷，張 云

1.東華大學 旭日工商管理學院，上海 200061

2.上海海洋大學 信息學院，上海 201306

3.東華大學 計算機科學與技術學院，上海 201620

多維不確定性XML數據模型的研究

王 艷1，2，樂嘉錦3，姜久雷1，張 云2

1.東華大學 旭日工商管理學院，上海 200061

2.上海海洋大學 信息學院，上海 201306

3.東華大學 計算機科學與技術學院，上海 201620

1 引言

近年來，大量技術被應用于海量數據的存儲和記錄，但是在很多情況下，數據本身存在錯誤或者不完整性，同時數據的源事件也是存在大量不確定性。

在數據庫領域對于不確定信息而言，最早是文獻[1]提出一種概率關系數據模型PRM及其關系代數，并在研究中用系統的觀點闡述了概率數據庫的有關理論，奠定了在數據庫中應用概率論來處理不確定信息的基礎。

后來，不確定的數據模型也被擴展到半結構化的XML數據。XML概率模型具備XML的靈活性，可以很自然地表示多個粒度的概率信息，乃至嵌套的概率信息；另外XML以其自描述性好與可擴展性高的優點，特別適用于信息抽取與數據集成等可能產生大量不確定信息的應用。

文獻[2]提出的P文檔模型（ProDB）是最早的概率XML數據模型，該模型描述節點的概率以父節點存在為前提，提出兄弟節點之間關系為相對獨立（ind）和相互排斥（mux）。文獻[3]和文獻[4]均擴展了P文檔模型，其中文獻[4]對原有的P文檔模型的邊增加了外部約束條件，利用約束條件來限制節點出現概率。文獻[5]對P文檔模型給出了高效的查詢算法。文獻[6]提出了一種XML概率樹模型，該模型給各節點附加一系列事件變量，由外部事件的發生的概率決定節點的存在性，增加了數據表示的靈活度。文獻[7]對概率樹模型進一步分析了查詢復雜度。文獻[8]提出了PXML模型，該模型是以有向圖為基礎的概率半結構數據模型，把概率實例定義為半結構實例及其對應的概率值。文獻[9]提出了以概率區間值表示PXML的數據模型。文獻[10]提出的概率樹模型以及文獻[11]提出的PrXML模型等對概率模型進行了進一步的擴充。

現有的XML概率模型在表達方式和表達效率上不斷演進，但是由于一直在單維空間進行表述，所以在描述復雜事件時依然存在一定缺陷。本文在目前已有的XML概率模型的基礎上，以建立描述多維復雜事件的概率數據模型為目標，建立一種新的關聯事件概率模型，并且提出了多維不確定概率模型空間的概念，從而使系統能對多個概率模型進行統一建模，并把單維XML概率節點引申到多維空間，進而定義了統一的空間查詢方式，從而優化了復雜事件的概率數據建模和查詢方法。

2 關聯事件概率模型

2.1 兩種經典概率模型

半結構化數據模型的出現，解決了不確定數據在無嚴格模式結構情況下的描述問題。在管理概率半結構化數據的方法基礎上，出現了直接以文檔樹形式描述的p-文檔模型[2]。如圖1所示，p-文檔模型以文檔樹的邊作為概率屬性的載體，各個節點的概率依附于上一級的概率，同時對于同層次節點之間，使用互斥或者獨立關系作為描述。節點和邊的數目決定了計算概率的工作量。

圖1 p-文檔模型結構圖

在計算節點概率的時候，按照下式：

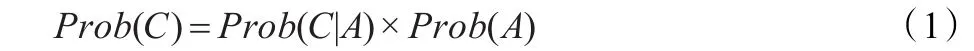
得到C節點的概率，同樣D節點的概率也可由公式（1）得到：

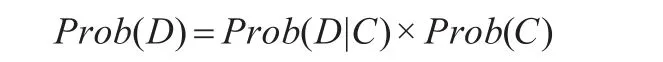
其中等式右邊的值可以從原XML文檔得到。所以計算某個元素e∈A，A為某個定義的子圖，只需要計算公式（2）：

其中n為從e節點到root節點r的所有路徑上的節點數目。

考慮了事件驅動后的概率樹模型[6]在各節點附加一系列外部事件變量，由外部事件的發生與關聯決定節點的存在性。按照概率樹的定義，數據樹t是一個4元組t=(A，E，r，φ)，A是一個節點有限級，E?A2，是以rootr∈A為起點的數據樹。φ作為字符串組對應的節點label標示。假設t=(A，E，r，φ)，t′=(A′，E′，r′，φ′)。可以說t和t′同構。假設有W作為有限事件變量級，存在概率條件為w或者-w， w∈W 。對于概率樹的定義T為4元組(t，W，π，Y)，t=(A，E，r，φ)是數據樹，π以W 的某種概率分布，Y分配概率條件到節點A-{r}。圖2是一個具體的概率樹模型結構圖，概率樹模型作為事件驅動的模型，它并不在各節點邊上附加概率值來描述不確定性，而是由事件的發生與否決定節點的存在性。

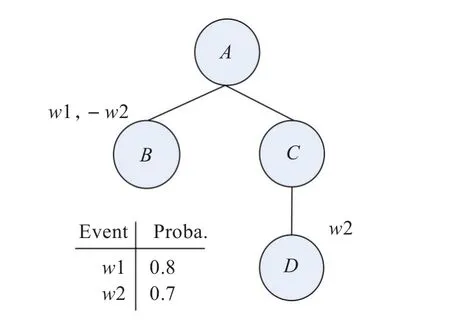
圖2 概率樹模型結構圖

圖2共有2個外部事件w1和w2，其發生概率分別為0.7和0.8。節點B出現的前提條件是事件w1發生且事件w2不發生；節點E存在的前提條件是事件w2發生。由于節點B與E的存在條件互斥，不存在同時包含節點B、E的子圖。包含且僅包含 A、C、D 3個節點的子圖的概率為：(1-0.8)×(1-0.7)-0.06，前提是w1、w2均不發生。

2.2 關聯事件有向圖概率模型定義

本文定義了一種概率有向圖模型，同時兼顧了前面描述的兩種經典模型的優點，并且擴展了表述概率事件的復雜度，從而提高了模型的表述能力。

定義1數據有向圖 f是一個4元組，表述為 f=(S，E，p，φ)，其中S是節點的有限集合，E?S2，作為節點有向圖，概率關系矩陣 p定義了所有節點的關系，φ標示了有限節點集合的字符串。

對于概率矩陣 p的定義為 pij=(ei-＞ej)節點i指向節點j的關聯概率，如果有A、B、C、D四個節點，形成的概率關系矩陣如公式（3）所示：

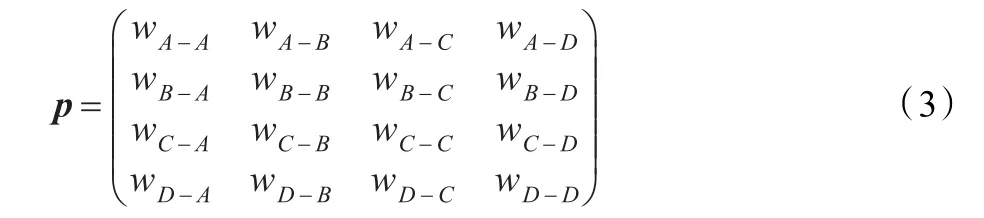
如果其中存在不相關的節點對，使用0表示。

對于某個節點B的概率Prob(B)，可以看作與之關聯的有向標識的集。

圖2的概率樹模型變換為如下關聯事件圖3，對于 A出現，B必然出現的節點關系，使用單向箭頭表示，把依存概率作為邊，對于C出現，B不出現，概率為 -1，箭頭的方向表示作用關系。不同節點通過外部事件關聯，如圖3所示。

計算節點B的概率，先確定有向標示的起點概率和標示概率的極性，然后計算。圖4中B節點的概率為：

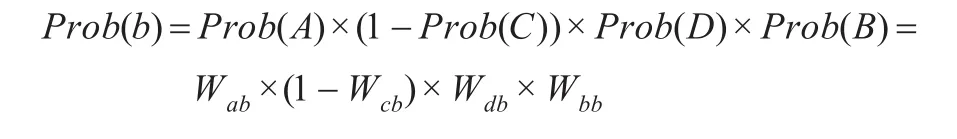
其中前面的Prob(A)，(1-Prob(C))，Prob(D)組成關聯概率，Prob(Wb)是內在節點事務驅動概率。

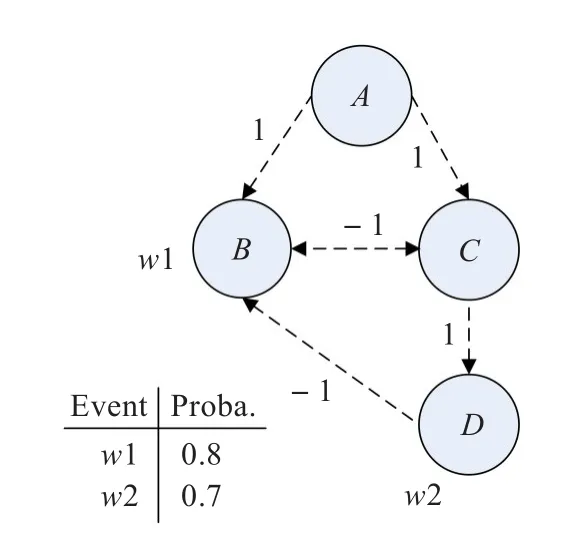
圖3 關聯事件概率模型結構圖

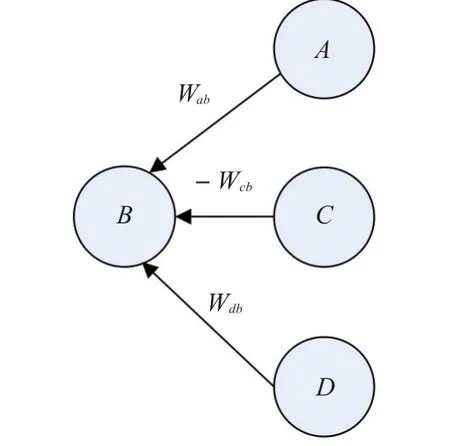
圖4 B節點的關聯事概率拓撲

所以，任何一個節點概率e可以由公式（4）計算為：

對于關聯事件有向圖概率模型，很明顯每個節點的關系從樹變成網，同時保留了外部驅動事件的影響。所以表述能力得到了提升，可以對更加復雜的概率數據進行描述。

3 多維XML概率模型空間定義與查詢

關聯事件的概率模型和其他概率模型均可以在多維平面展開，形成對于多維事件驅動的概率表述，從而極大地擴展了其復雜性。

定義2對任何一個節點的概率，有一個n維概率坐標表示，(P1，P2，…，Pn)，其中對于每一個坐標，表示在某一個該節點所在概率空間的概率坐標。對于該節點的概率，可以看作是在n維概率空間的某個點。

如果O(i)表示某個節點的概率坐標的維度。如果i點有4個坐標點，表示坐標維度為4，如果4維坐標的其中一個坐標值為1，O(i)=O(i-1)，出現降維事件。

對于每個概率空間，存在某一個概率模型，表示該節點的位置。假設Mi是第i維空間概率坐標形成的模型，Mj是第 j維空間概率坐標形成的模型，如果Mi∩Mj=0，則稱為 Mi正交于Mj，其中∩操作表示兩個模型的節點之間關系∩，或者說兩個模型非聯通。如果 Mi非正交于Mj，則稱為節點i所處的概率空間存在聯通性。需要通過聯通關系裁剪概率空間，保證正交，或者降低坐標維度。

關聯事件模型M1和p文檔模型M2對每個點的概率模型疊加，如圖5所示。

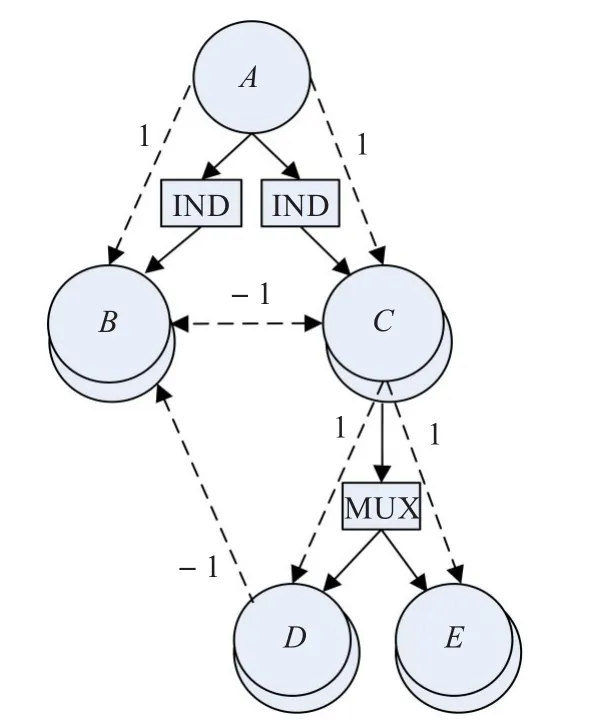
圖5 多維概率模型疊加結構圖

對于每一個節點的概率坐標Pnode=(Pp，Pw)，其中Pp是由P-文檔模型定義的，Pw由概率樹事件定義。

在引入多維概率模型以后，進而描述多維空間的操作運算和關于節點的概率坐標的幾個延伸，如下定義。

定義3對某個節點的概率坐標，形成坐標向量Pi，定義坐標概率權重向量：

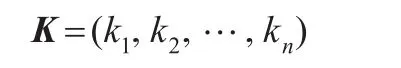
K'i，Pi作為權重因子以后的節點概率坐標。對于正交模型空間的節點 X每個坐標 pi，如果存在一個時間函數，在t時刻，發生關系，假設存在函數 F(t，pi)，在t時刻，坐標 pi可以映射到 pj上，則稱為概率模型i和 j在節點X上存在時間滑動映射關系，pj=F(t，pi)，其中F為時間滑動概率函數，對于實際世界，不同的概率模型在某個節點是存在某種關聯的，?t，pj=F(t，pi)，則概率模型空間i和 j是可以一一映射的，同時O(i)=O(i-1)，存在降維事件。

下面對于關聯事件概率模型與概率模型空間進行查詢研究。首先定義查詢類型。對于關聯事件概率模型，作為網狀關聯模型，需要給出并且評估有效的查詢方法。為了定義一種查詢方式，首先定義子關聯圖的概念：

定義4有 f=(S，E，p，φ)和 f′=(S′，E′，p′，φ′)兩個關聯事件圖，如果有：

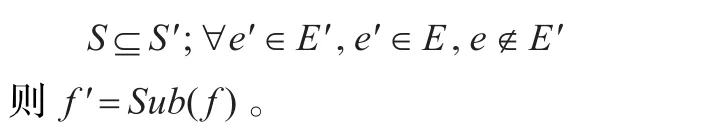
對于一個查詢節點e的操作，定義為Q(e|f)，對于Q(e′|f′)= Q(e|f)∩Sub(f′)，定義Prob(e|f)=Prob(e|fmin)，其中fmin=sub(f)，fmin是元素最少的sub(f)，則稱 fmin是e的最簡子關聯圖。

對于具有多維概率坐標的節點，首先獲得正交概率空間，得到Omin。

對每個空間實施Qi(e)函數，獲得全部維度的查詢信息。

對概率世界的查詢可以表示為：

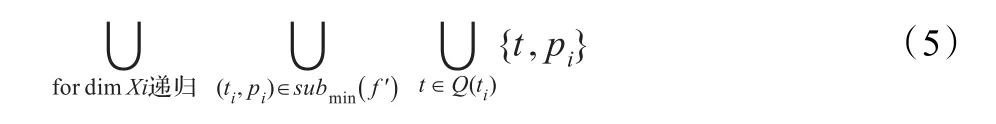
其中S={(ti，pi)}，作為PW集。

在多維概率模型以及概率模型的引申定位，從空間上統一了多種概率模型。對于節點的多模型多概率定義創造性地給出了統一建議，使得表述和兼容性在多維度下統一，也就是在兼容性和統一性上有很大改善和提升。

多維概率模型對于查詢的復雜度并不能降低，而是在于表述能力的提升。需要指出的是在降維操作之后的查詢復雜度才是最終的可度量查詢復雜度。對于復雜度本身可以同樣適用矩陣和向量表示。

4 多維概率模型實例分析

以某大學人事數據為例。圖6列出了一個2維概率模型的實例。可以看到，在維1（黑影部分），通過類似P-文檔模型結構表示了某大學人事數據概率模型各個節點的關系。而對于維2（灰色部分），是同樣節點的外部概率事件模型。對于每個節點，存在二維概率值，例如對于salary value的劃分概率，不只是由工資級別決定的，同時與職位存在外部事件關聯。

圖6 多維概率模型實例

在假設的概率關系中得到一個節點二維矩陣如下：

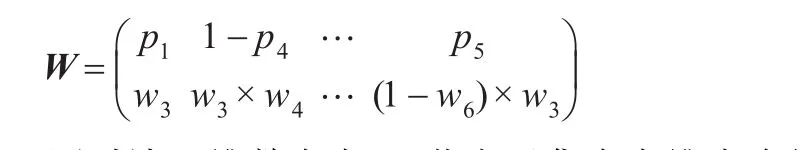
同時該二維數存在W1節點子集存在維度降低，為1維概率節點集：

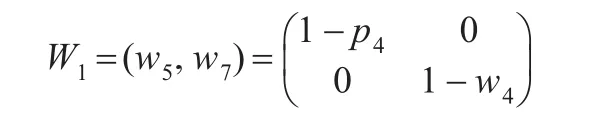
存在W0節點子集存在更大的維度減低，為0維概率節點集：

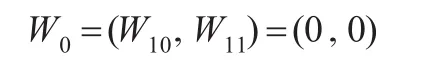
剩余的子集為2維節點子集W2，由此可以將W形成3類矩陣進行計算，3類矩陣的計算復雜度一次增加。

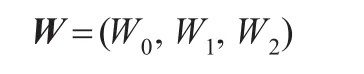
可見同一節點由于存在多重空間表示，表述性必然增加。但是降維以后的操作和查詢復雜度是由節點本身的關聯復雜度導致的。隨后對二維空間的每個維度概率節點，可以實施前文定義的多維查詢函數，獲得全部維度的查詢信息。多維查詢函數是在之前多維模型的同步維度擴展，并不作為重點在本文描述。

在本實例中可見二維查詢函數存在一個可優化之處。對于每個模型通常是既定的，并沒有考慮正交性，也很難進行正交分解，所以在非正交化概率模型間的查詢效率簡化是值得進一步研究的。

5 結束語

隨著計算機與網絡技術的蓬勃發展，海量的數據展現在人們面前，大量的不確定數據需要有高效的管理，并且要能為用戶提供方便、有效、真實的查詢，概率則恰是表示不確定信息的一種常用方式，因此對概率數據模型進行研究有著很重要的應用價值。

本文描述了一種XML關聯事件概率數據模型，能夠描述較為復雜的概率數據模型并提出概率模型空間的概念和查詢，使系統能夠使用多個概率模型進行建模，把每個XML概率節點引申到多維空間，進而定義了統一的查詢方式，為復雜概率數據建模和查詢優化提供了一種新穎的理論方法。

后續多維概率模型的維度正交化研究以及在非正交性的既定概率模型下的最大查詢簡化方法研究，是下一步的研究工作。

[1]Dey D，Sarkala S.A probabilistic relational model and algebra[J].ACM Transactions on Database Systems，1996，21（3）：339-369.

[2]Nierman A，Jagadish H V.ProTDB：probabilistic data in XML[C]// Proceedings of 28th International Conference on Very Large Data Bases，2002：646-657.

[3]Kimelfeld B，Sagiv Y.Matching twigs in probabilistic XML[C]// VLDB’07，Vienna，Austria，2007：27-38.

[4]Cohen S，Kimelfeld B，Sagiv Y.Incorporating constraints in probabilistic XML[C]//Proceedings of the 27th ACM SIGMODSIGACT-SIGART Symposium on PrinciplesofDatabase Systems，Vancouver，2008：109-118.

[5]Souihli A，Senellart P.Efficient query evaluation over probabilistic XML with long-distance dependencies[C]//Proceedings of the 2011 Joint EDBT/ICDT Ph.D.Workshop，Sweden，2011：32-37.

[6]Abiteboul S，Senellart P.Querying and updating probabilistic information in XML[C]//10th InternationalConference on Extending DatabaseTechnology，Munich，Germany，2006：1059-1068.

[7]Senellart P，Abiteboul S.On the complexity of managing probabilistic XML data[C]//Proceedings of the 26th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems，Beijing，2007：283-292.

[8]Hung E，Getoor L，Subrahmanian V S.PXML：a probabilistic semistructured data modeland algebra[C]//Proceedingsof the 19th International Conference on Data Engineering（ICDE），2003：467-478.

[9]Hung E，Getoor L，Subrahmanian V S.Probabilistic interval XML[J].ACM Transactions on Computational Logic，2007，8（4）.

[10]van Keulen M，de Keijzer A，Alink W.A probabilistic XML approach to data integration[C]//Proceedings ofthe 2lst IEEE International Conference on Data Engineering，Tokyo，2005：459-470.

[11]Kimelfeld B，Kosharovsky Y，Sagiv Y.Query efficiency in probabilistic XML models[C]//Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data，Vancouver，2008：701-714.

WANG Yan1，2,LE Jiajin3,JIANG Jiulei1,ZHANG Yun2

1.Glorious Sun School of Business and Management,Donghua University,Shanghai 200061,China
2.College of Information Technology,Shanghai Ocean University,Shanghai 201306,China
3.School of Computer Science and Technology,Donghua University,Shanghai 201620,China

Uncertainty of mass data storage and recording and the extensive application of XML in the extension make that the XML association event probability data model has become a hot topic.Based on the existent probability models,this article describes the complex event probabilistic data model,and puts forward the conception of multidimensional uncertainty probability model space.Furthermore,the paper unifies modeling of multiple probability models,and extends the single dimension XML probability node to multidimensional space,and then defines the uniform spatial query,provides a new theory method of modeling and query optimization of complex probabilistic data model.

Extensive Markup Language（XML）;uncertainty;multi-dimensional space;probability model;related events

不確定海量數據存儲與記錄的廣泛應用及其在XML上的擴展，使XML的關聯事件概率的數據模型研究成為研究熱點，以描述復雜事件的概率數據模型為目標，在當前已有概率模型的基礎上，提出了多維不確定概率模型空間的概念，基于多個概率模型進行統一建模，并把單維XML概率節點引申到多維空間，進而定義了統一的空間查詢方式，為復雜概率數據建模和查詢優化提供了一種新穎的理論方法。

可擴展標示語言（XML）；不確定性；多維空間；概率模型；關聯事件

A

TP309.2

10.3778/j.issn.1002-8331.1203-0174

WANG Yan,LE Jiajin,JIANG Jiulei,et al.Research on multi-dimensional uncertainty data model based on XML.Computer Engineering and Applications,2013,49（23）：91-94.

上海市科學技術委員會專項基金資助項目（No.11510501300）。

王艷（1978—），女，博士研究生，講師，主要研究方向：信息管理與信息系統、數據挖掘等。E-mail：yanwang@shou.edu.cn

2012-03-07

2012-05-21

1002-8331（2013）23-0091-04

CNKI出版日期：2012-07-16 http://www.cnki.net/kcms/detail/11.2127.TP.20120716.1501.040.html