基于排隊論的工程裝備戰時維修力量配置

魯冬林，張 強，邸彥朝，曹建偉，張紅鋒

(1.解放軍理工大學，南京 210007;2.解放軍邊防學院 邊防管控教研室，西安 710108)

工程裝備在執行工程保障任務時，特別是在戰爭中，會受到不同程度的損壞，嚴重降低了裝備的工程保障效率。因此，對戰損工程裝備的戰場搶修成為戰時維修重要內容。在戰爭的準備階段，必須充分考慮工程裝備的維修力量的配置，以減少維修力量配置不足或過剩，從而達到維修力量的合理配置。

目前，大多維修排隊模型考慮的是工程裝備數量無限多的情況。而實際運用時，工程裝備的數量是有限的，而且維修站的容量也是有限的，因此，其模型有一定的局限性。目前對工程裝備戰時保障力量的配置研究還很少。在此充分考慮到參加戰時工程保障任務的工程裝備的數量有限，建立了顧客數量有限的排隊模型。并在排隊論的基礎上引用了戰時工程裝備的平均故障臺數、等待修理的平均臺數、裝備的完好率，通過限制不同損壞程度的工程裝備的完好率，獲得了針對不同損壞程度的工程裝備的戰時維修力量配置，最終獲得戰時維修力量總配置。

1 維修排隊模型選取

1.1 排隊論模型一般形式及數量指標

排隊是日常生活中的常見現象，如顧客到商店購物、客戶到銀行接受服務等。當顧客數超過服務機構(服務器、服務臺、服務員)的容量時，到達的顧客不能立即得到服務，因此就產生顧客等候的情況，即排隊現象。一般來說顧客的到達是隨機的，因此排隊論又稱隨機服務系統理論。

1)排隊模型的一般形式。X/Y/Z/A/B/C，其中:X 表示顧客相繼到達間隔時間分布;Y 表示服務時間分布;Z 表示并列的服務臺數目;A 表示服務系統的容量限制;B 表示顧客源數目m;C 表示服務規則，如先到先服務(FCFS)，后到后服務(LCFS)。

2)排隊模型的數量指標。對長:指在系統中的顧客數，其期望值記作Ls;排隊長:指在系統中排隊等待服務的顧客數，其 期 望 值 記 作 Lq。到達率:指單位時間內到達系統中的顧客數，其期望值記作λ;服務率:指單位時間系統中每個服務臺所服務的顧客數，其期望值記作μ。

1.2 維修排隊模型選取的依據

一般情況下，工程裝備的維修服務由多個維修維修力量編組而成，并遵循先到先服務的維修規則，維修點的最大容量有限，維修裝備源有限，且裝備針對一個維修服務點的進行維修循環(即戰損后再次送往維修點維修)。

工程裝備到達率λ 服從負指數分布為簡化模型，對于工程裝備而言，視其損壞后即刻送達維修站維修，工程裝備損壞的時刻滿足以下4 個條件［1］:

1)在不相重疊的時間區間內工程裝備損壞是相互獨立的。

2)對于規定時間間隔Δt，在時間區間［t，t +Δt)內有1個裝備損的概率與t 無關，且視為與時間區間Δt 成正比，即p1(t，t+Δt)=λΔt+ο(Δt)，其中ο(Δt)，當Δt→0 時，是關于Δt 的高階無窮小。λ ＞0 是常數，它表示一個單位時間裝備到達維修站的概率。

3)對于規定時間間隔Δt，在時間區間［t，t +Δt)內有2個或者2 個以上工程裝備到達的概率小。

4)工程裝備的到達是純隨機的，無記憶性。

因此，工程裝備的到達率服從負指數分布。維修率μ 服從泊松分布。對于某臺工程裝備的維修時間，在固定人員配備的情況下，維修人員對工程裝備的維修時間滿足上述前3條。由于人員對工程裝備的維修時間隨著經驗的增長而維修時間變短，因此維修時間不滿足無記憶性。則維修時間服從泊松分布。

由上述分析，工程裝備維修系統排隊模型可表述為M/M/c/m/m;其參數依次為:顧客到達服務臺的時間服從負指數分布(M 表示)，服務時間服從泊松分布(M 表示)，服務臺個數為c，服務系統容量為m，顧客總體為m。

2 工程裝備維修服務排隊模型

2.1 維修排隊模型的構建

M/M/c/m/m 排隊系統模型可表示如圖1 所示。建立M/M/c/m/m 排隊模型的狀態轉移圖(圖2)，其中第n 個狀態表示系統中有n 臺工程裝備，φ 為維修力量合并后相對于總維修力量變化的影響系數。兩相同維修力量合并后而成的維修力量為總維修力量的60% ～80%。

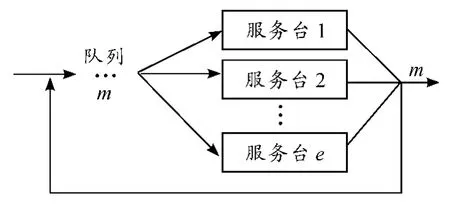
圖1 M/M/c/m/m 排隊系統模型

圖2 狀態轉移圖

根據狀態轉移圖列出狀態轉移方程:

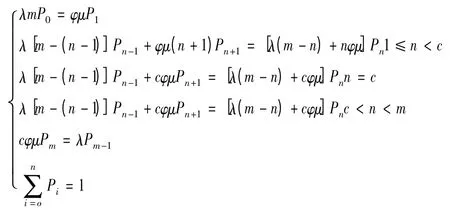
求解得差分方程:

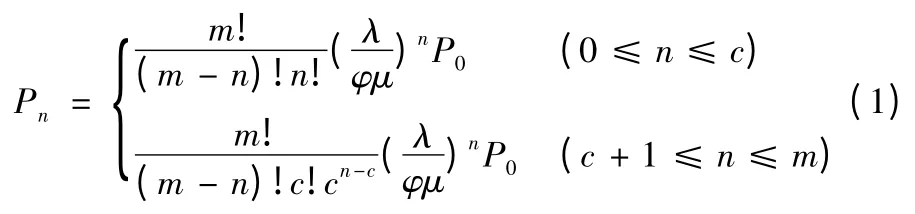
其中:

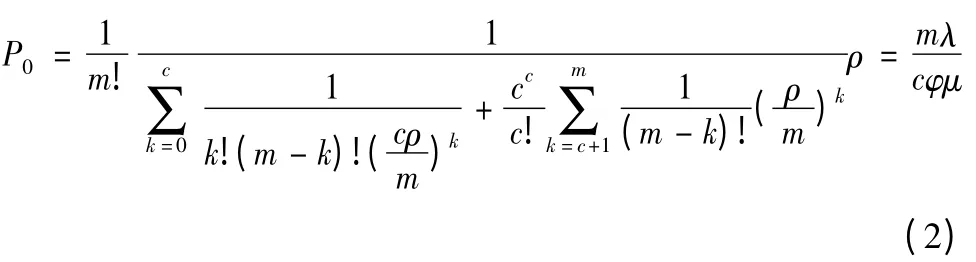
由排隊論的基本理論，定義隊長度等于工程裝備平均故障臺數，排隊長等于工程裝備排隊等待維修的平均臺數。

1)等待修理的平均臺數:

2)平均故障臺數:

2.2 工程裝備維修排隊模型參數獲取

首先，裝備平均到達率λ 的獲取。一是可以通過人員到實際地域調查獲取。二是通過對到達維修站的工程裝備數量的統計獲得。其次，工程裝備的平均維修率μ，主要是通過對該維修所的人員進行綜合評價獲取。

2.3 裝備完好率

工程裝備完好率是反應裝備技術狀況的指標，它是完好裝備與實有裝備之比率。工程裝備完好率可以按裝備臺數來計算，稱裝備數量完好率;也可以按裝備臺日數來計算，稱裝備臺日完好率。本文定義裝備的數量完好率。

設參加某工程保障任務的工程損壞裝備有m 臺，其中有Ls臺裝備由于故障正在等待維修。則工程裝備的完好率可定義為:

3 實例分析

工程裝備戰時損傷可以分為輕度損壞、中等損壞、嚴重損壞。根據資料統計，對于輕度損傷裝備，一般需要一個維修小組進行2 h 維修(現場維修);對于中度損傷裝備，需要一個維修小組進行4 h 維修(定點維修);對于重度損傷的裝備，需要一個維修小組進行24 h 維修(定的維修)。視工程裝備一個維修小組具有維修力量量化為1(單位維修力量)，視工程裝備單位維修力量為工程裝備戰時維修力量的最小模塊化單元。通過配置單位保障力量即可獲得工程裝備的戰時保障力量。

設某戰區動用100 輛工程裝備為部隊遂行工程保障，據歷史數據統計，工程裝備的故障間隔時間服從負指數分布，平均無故障時間為30 h，即工程裝備的平均無故障率λ 為0.033 3臺/h。伴隨保障服務時間服從泊松分布，對于輕損裝備的維修時間為2 h，即平均修復時間μ輕=0.5 臺/h;對于中損裝備的維修時間為4 h，即平均修復時間μ中=0.25 臺/h;對于重損裝備的維修時間為24 h，即平均修復時間μ重=1/24 臺/h。假設要求對輕損裝備的完好率保持在90%以上，中損裝備的完好率保持在80%以上，重損裝備的完好率保持在60%以上。配備戰時保維修維修力量。

由于不同損傷裝備的維修率不同，可針對不同裝備的損傷數目分別求出其維修力量，最后求得總維修力量。根據戰損比例，100 臺工程裝備在遂行工程保障任務中的不同程度損傷的臺數:輕損裝備40 臺，中、重各損壞15 臺，另外15 臺報廢(不進行維修)。

根據M/M/c/m/m 可計算得，計算結果如圖3 所示:輕損裝備(m=40)完好率要保持到90%以上至少需配備c =3個維修力量;中損裝備(m=30)完好率要保持80%以上至少需c=4 個維修力量;重損裝備(m =15)完好率不能達到60%以上。為此，在配置重損裝備的維修力量時，將兩個維修力量合并到為1 個維修力量，取影響系數φ =0.75。則兩個維修力量合并后維修力量為1.5，因此2 個維修力量合并后對重損裝備的平均修復時間μ重=1/18 臺/h。經計算得重損裝備的維修力量配置圖(圖4)，重損裝備(m =15)完好率不能達到60%以上，需要配備2 ×7 =14 個維修力量。

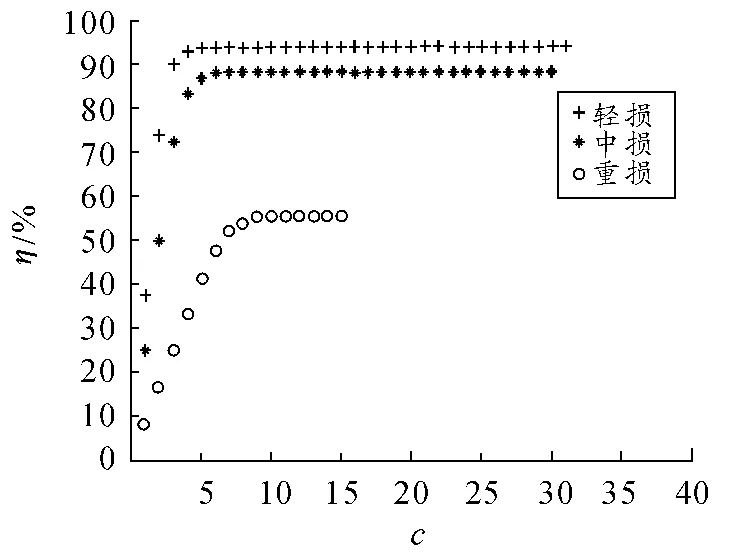
圖3 維修力量未合并前戰損裝備維修力量配置

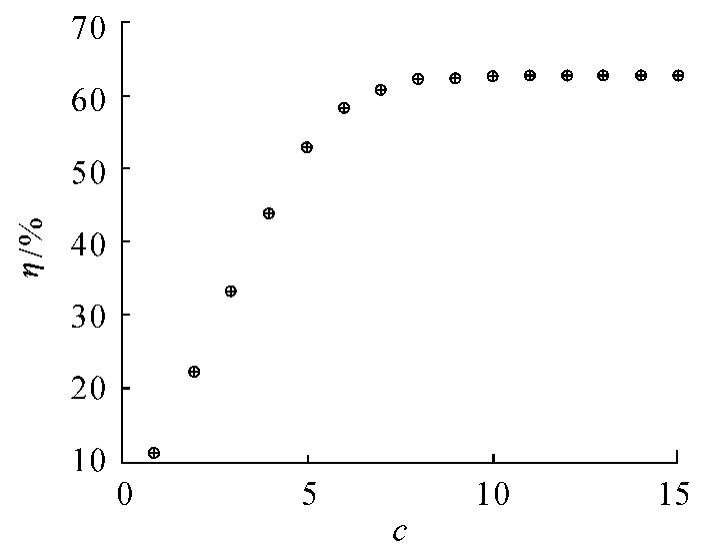
圖4 合并維修力量后重損裝備維修力量配置

4 結束語

在模型中，通過多戰時工程裝備的總數的限制。修正了其他模型的不足，更加結合實際運用。根據上述事例分析，在戰時維修力量的配置時，若保障要求嚴格，可能導致現有的單位保障力所具有保障效率量不能完成保障任務，因此需要將維修力量合并，但需考慮維修力量合并后的變化(并不是維修力量的簡單疊加)。如實例所訴，當重損裝備在單位保障力為1，無論怎樣提高保障力的數量，任然不能使裝備的重損裝備的完好率達到60%，原因是提高的維修力沒有得到充分利用，多余的維修力量處于空閑狀態。因此在講2 個維修力量合并到一起后可以縮短重損裝備的平均維修時間，最后從新配置維修力量即可使得重損裝備的完好率達到60%。

［1］甘應愛，田豐.運籌學［M］.第3 版.北京:清華大學出版社，2005.

［2］宋瑜.商業銀行營業網點排隊系統設計與實現［M］.大連:大連理工大學，2008.

［3］張忠斌，王精業.基于排隊論的裝甲裝備維修力量預測建模研究［C］//哈爾濱:中國系統仿真學會第五次全國代表大會2006 年全國學術年會論文集，2006.

［4］林健，馬振書，黃剛，等.基于排隊論的可修件維修模型［J］.價值工程，2011（7）:32-33.

［5］JIA J，LIU S. Research of the expended downtime for repairable system with single repairman cacation［J］.Systems Engineering and Electronics，2006，28（11）:1770-1774（in Chinese）.

［6］賈治宇.基于停機時間的復雜系統維修資源配置模型研究［C］//全國現代制造集成技術學術會議論文集，2010.

［7］張會賓.基于排隊論的車輛維修保障中維修組個優化［J］.兵工自動化，2007（2）:20-22.

［8］王小飛，蘇凡囤，王海濤，等.基于排隊論的戰時工程裝備搶修任務調度［J］.兵工自動化，2012（10）:29-32.