某迫榴式火炮反后坐裝置的結構優化及分析

宋 焦，何 永，趙 威，陶齊岡

(南京理工大學 機械工程學院，南京 210094)

反后坐裝置是火炮關鍵部位之一，其性能直接影響火炮的結構受力和發射時動態響應。因此，開展關于反后坐裝置基于受力優化的結構優化設計，具有十分重要的意義。本文利用ISIGHT 軟件開展了對某迫榴式牽引火炮反后坐裝置的結構優化，其目的是使得后坐力平穩，從而降低結構受力，有利于減輕全炮質量，并提高火炮的射擊穩定性［1-3］。

1 后坐受力分析及動力仿真

1.1 迫榴炮后坐受力分析

本文所研究的某超輕型迫榴式牽引火炮，反后坐裝置采用傳統的節制桿式制退機和液體氣壓式復進機。后坐部分通過反后坐裝置與炮架彈性連接，射擊時沿搖架導軌作后坐、復進直線運動。后坐時后坐部分受力示意圖如圖1所示。

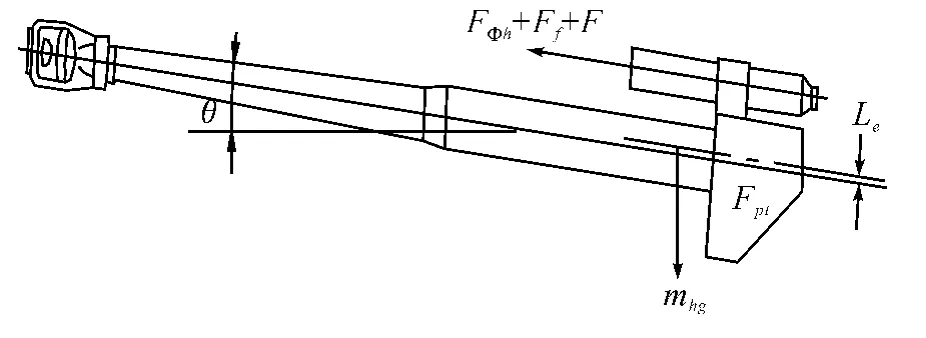
圖1 后坐時后坐部分受力分析

火炮發射時后坐部分的主動力為炮膛合力Fpt、后坐部分重力mhg 和彈丸作用于膛線導轉側力矩Mhz;約束反力為制退機力Fφh、復進機力Ff和摩擦力F［4］。炮膛合力由火藥氣體和彈丸彈帶共同作用產生，膛內時期可表示為

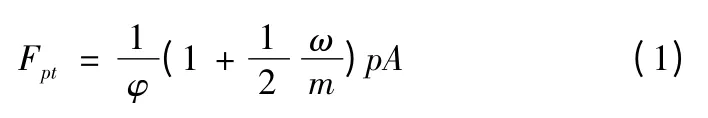
式中:φ 為次要功計算系數;ω 為裝藥質量;m 為彈丸質量;p為膛內平均壓力;A 為線膛部分截面積。

液體氣壓式復進機力Ff可表示為

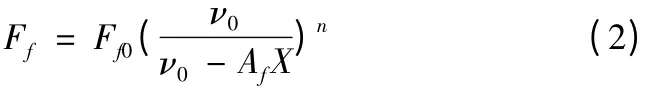
式中:Ff0為復進機初力;ν0為氣體初體積;Af為復進機活塞工作面積;X 為后坐行程;n 為多變指數，取決于復進機的散熱條件和活塞運動速度，一般取n=1.3。

節制桿式制退機的結構原理圖如圖2 所示。

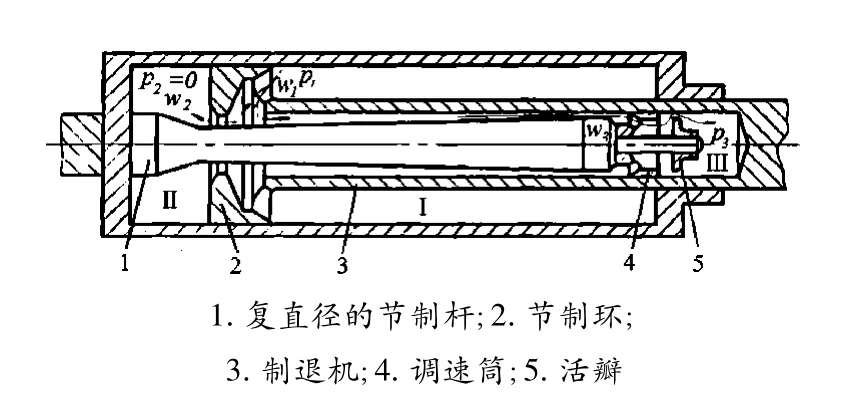
圖2 節制桿式制退機的結構原理

節制桿式制退機，桿后坐時，制退機液壓阻力可表示為

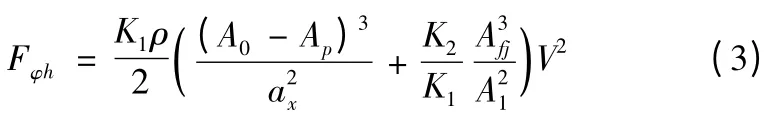
其中:K1為主流壓阻力系數;ρ 為流液密度;K2為支流阻力系數;A0為制退機活塞工作面積;Ap為節制環孔面積;Afj為復進節制器工作面積;A1為支流最小截面積;V 為后坐速度;ax為流液孔面積，為節制環內徑，dx為節制桿任意截面直徑。

假設:①發射時所有力均作用在射面內;②后坐部分和除此以外的炮架部分均為剛體;③忽略彈丸作用于膛線導轉側力矩作用［4］。則發射時后坐部分受力可簡化為剛體在平面力系作用下動力學問題。取火炮后坐的方向為x 方向，在該方向對后坐部分運用牛頓第二運動定律，則后坐運動方程可表示為

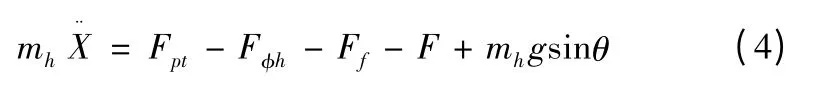
式中:X 為后坐行程;θ 為火炮高低射角。

定義后坐阻力FR為

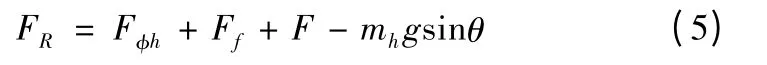
則式(4)可簡化為

在火炮內彈道條件一定情況下，后坐阻力變化與后坐運動和火炮受力有很大關系。

1.2 后坐運動動力仿真結果

本文根據以上公式等編制了仿真計算程序，對該新型120 mm 口徑迫榴炮方向射角為0°，高低射角為0°時進行仿真，計算結果如圖3、圖4 所示。

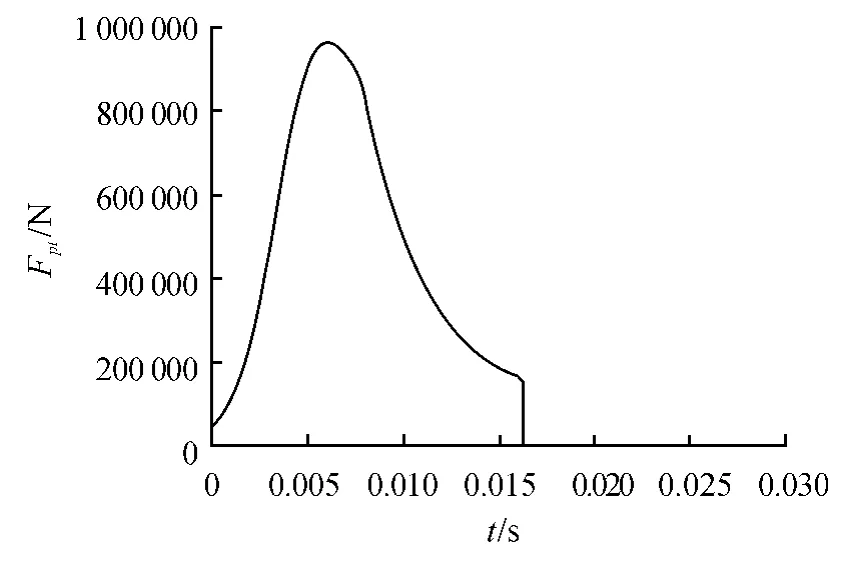
圖3 炮膛合力—時間曲線

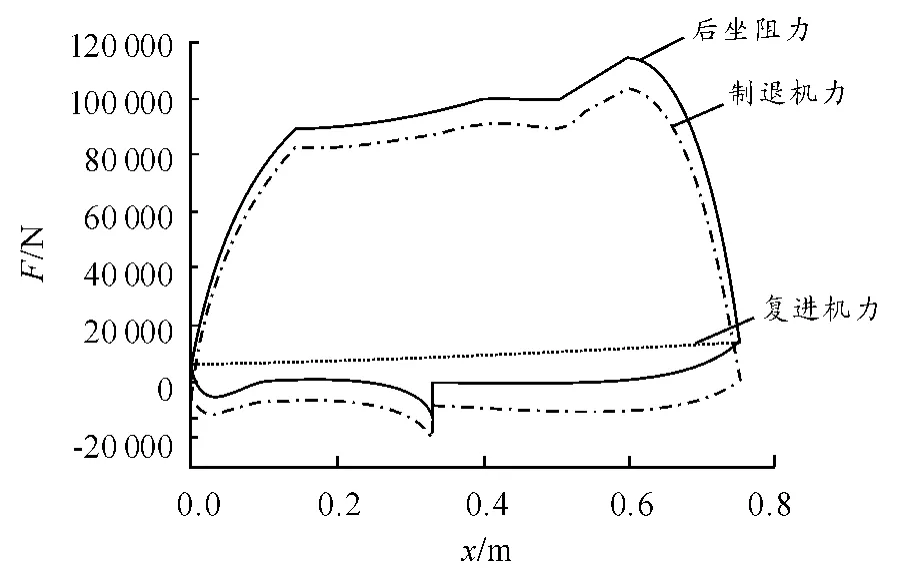
圖4 后坐阻力、制退機力、復進機力—位移曲線

圖3 為炮膛合力曲線，最大值Fptmax為976 kN。圖4 中后坐阻力由制退機液壓阻力、復進機力和摩擦力組成，曲線呈前低后高的趨勢，最大值FRmax為115.17 kN，使得火炮結構受力不盡合理，需進行優化。

2 反后坐裝置結構優化

2.1 優化模型建立

對反后坐裝置優化時，一般不優化復進機，只優化制退機［5］。由圖2 節制桿式制退機的結構原理圖和式(3)可知制退機力是流液孔ax和V 的函數，而ax與節制桿尺寸相關，故對節制桿尺寸進行調整，可獲得理想后坐阻力曲線。

本文對火炮方向射角為0°，高低射角為0°時的后坐阻力進行優化，建立的優化模型如下。

1)目標函數

選取后坐阻力峰值最小為目標函數，可表示為min FR。

2)設計變量

將節制桿各段的折點直徑d1，d2，…，dn及各段軸向尺寸x1，x2，…，xn作為設計變量，設計變量有2n-1 個［6］。

3)約束條件

由于后坐長度受限制，需對后坐長λ 進行約束。為了節制桿在設計時其徑向尺寸不小于節制桿最小尺寸dmin，且節制桿能順利通過節制環，需對節制桿徑向尺寸進行約束。為了每次計算有效，對節制桿各段軸向尺寸也需要進行約束。優化時節制桿仍需保證壓桿穩定性。本優化具體約束條件

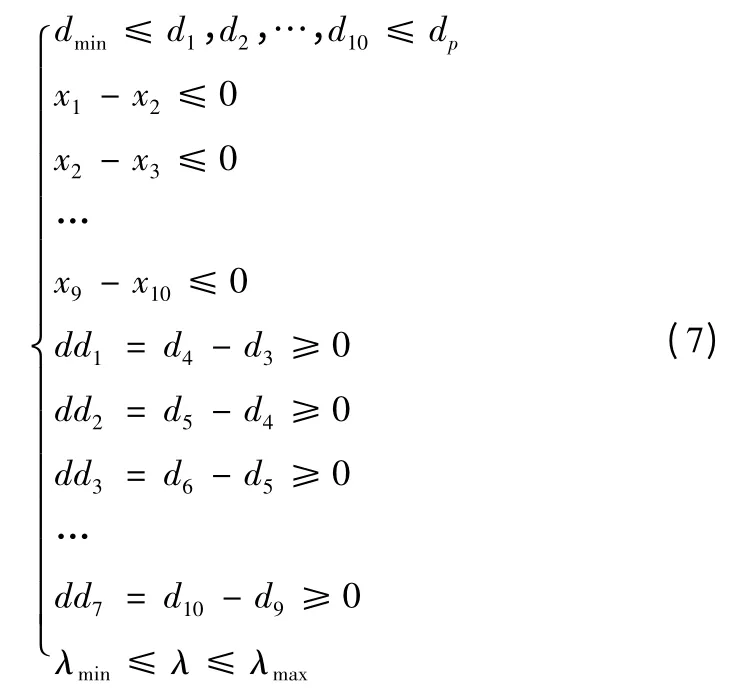
2.2 優化模型實施

本文利用多學科優化軟件ISIGHT 集成后坐FORTRAN計算程序建立優化模型，選用修正可行方向法(Modified Method of Feasible Directions-ADS)進行求解，流程如圖5 所示。ISIGHT 集成FORTRAN 運行程序如圖6 所示。其中輸入文件被替換為jzg.dat，執行文件被替換為可執行的FORTRAN 程序文件Recoil_shandi. exe，輸出文件被替換為RESULT.DAT。過程集成完成后，在參數表中對設計變量、約束函數和目標函數進行設定。

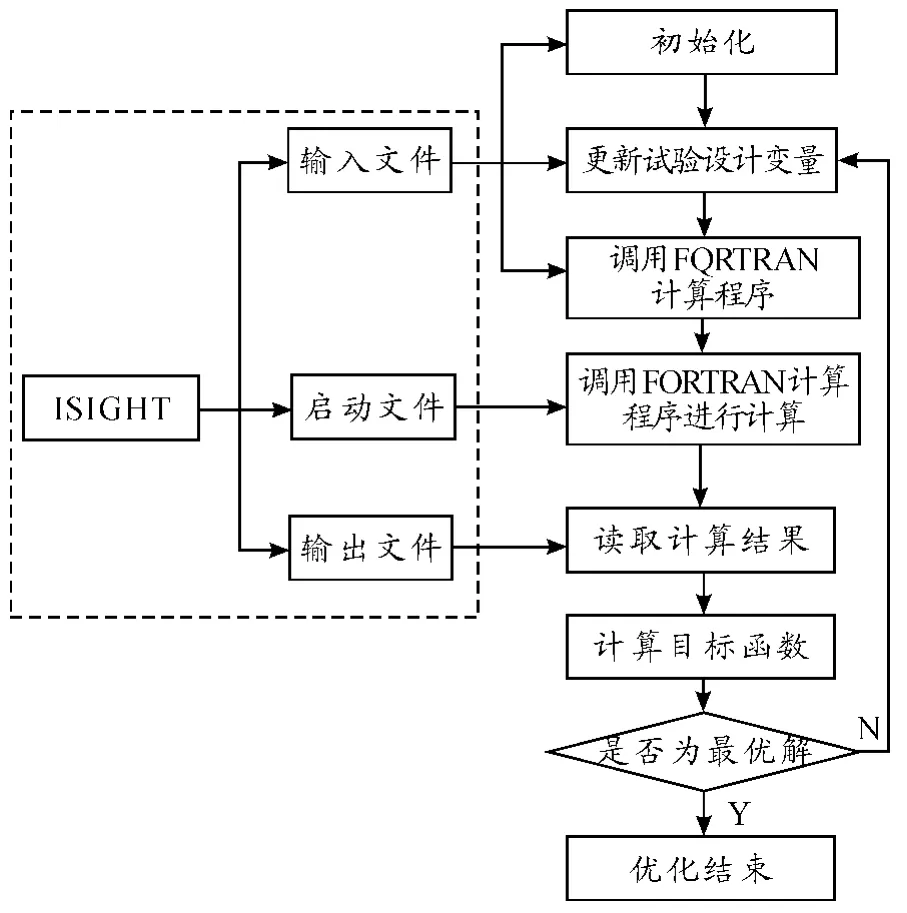
圖5 ISIGHT 集成FORTRAN 優化流程

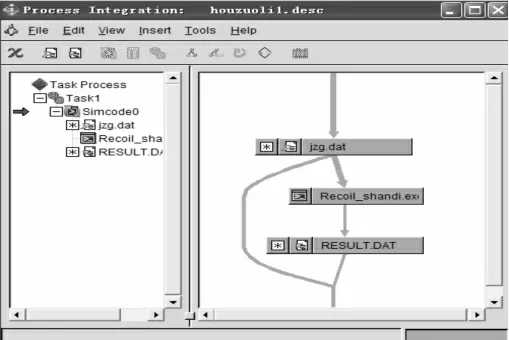
圖6 ISIGHT 集成FORTRAN 運行文件

3 仿真結果及分析

本文通過ISIGHT 軟件對火炮方向射角為0°，高低射角為0°時的后坐阻力進行優化。初始和優化后后坐阻力—時間曲線及后坐阻力—位移曲線圖如圖7、圖8 所示。

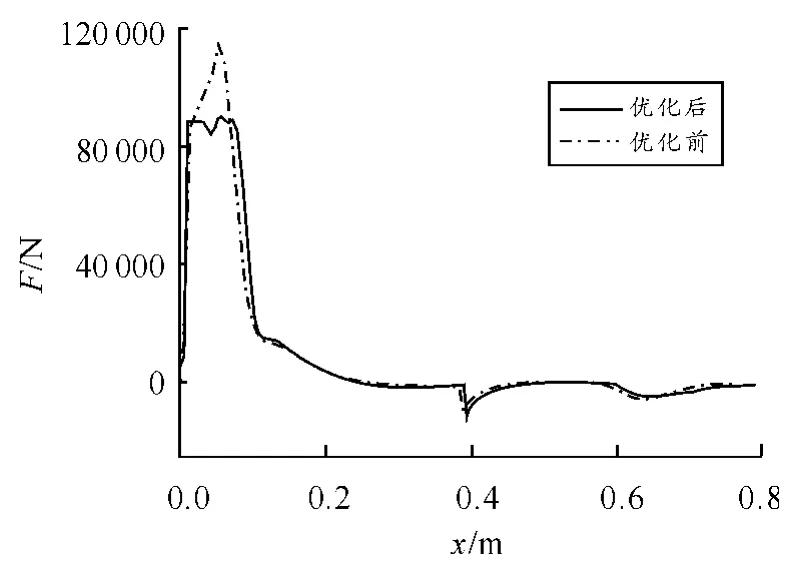
圖7 后坐阻力-時間圖

圖8 后坐阻力-位移圖

由圖7、圖8 可知，后坐阻力曲線更加平緩，后坐阻力峰值由115.17 kN 降低為90.01 kN，優化前后總體后坐能量基本一致。以上仿真曲線說明通過調節節制桿參數，可以獲得較優的后坐阻力曲線。

4 結束語

本文在對反后坐裝置進行受力分析的基礎上，編寫了FORTRAN 計算程序對后坐運動進行仿真，運用ISIGHT 軟件集成FORTRAN 計算程序建立優化模型并進行仿真優化。仿真發現該優化模型通過對節制桿尺寸的參數優化，獲得了較優的后坐阻力曲線。該優化模型可以減小后坐阻力峰值，使后坐力更平穩，從而降低結構受力，有利于減輕全炮重量和提高火炮射擊穩定性。

［1］李強，鄭建國，高樹滋.火炮穩定性與后坐阻力R 的最優設計［J］.火炮發射與控制學報，1997（1）:34-39.

［2］宗士增，錢林方，徐亞棟.火炮反后坐裝置動力學耦合分析與優化［J］.兵工學報，2007（3）:272-275.

［3］何永，楊軍榮，高樹滋.曲線后坐火炮后坐阻力規律的分析與研究［J］.南京理工大學學報，1997（4）:217-220.

［4］高樹滋，陳運生，張月林，等.火炮反后坐裝置設計［M］.北京:兵器工業出版社，1995.

［5］鄭小將.駐退機優化設計［D］.南京:華東工學院，1990.

［6］周成，顧克秋，邵躍林.火炮制退機節制桿優化設計［J］.火炮發射與控制學報，2012（4）:68-69.