火箭助飛魚雷入水點精度Bayes點估計評定方法

邵宗戰，侯代文，房 毅

(91439 部隊，大連 116041)

在入水點精度評估中，使用最多的是假設檢驗方法。該方法在代價函數最小準則下，先假設總體參數的分布形式，然后利用試驗信息計算似然概率，進而確定接收原假設還是備擇假設。假設檢驗方法在拒絕原假設時有充分的理由，但是在不能拒絕原假設時卻沒有足夠的理由接受原假設，而工程檢驗的目的是要確認所關心的原假設是否成立，或者說待檢驗的產品是否合格，因此假設檢驗方法難以滿足工程實踐的需求。特別地，在入水點精度的考核中，假設檢驗方法一般將入水點偏差信息通過落入圓的劃定轉化為服從二項分布的成敗型問題進行簡化處理，在接受原假設時，不僅意味著不拒絕原假設，還可能會因為所作假設的差異，得到截然不同的結論;而且將精度問題簡化為成敗型問題，在客觀上也造成入水點信息的損失，因此假設檢驗方法難以滿足工程實踐的需求［2］。

參數估計方法將入水點偏差看作服從某一分布函數的隨機變量，利用試驗信息估計變量的值，不僅解決了假設檢驗方法中接收原假設時的充分性問題，而且避免了入水點信息的損失。采用經典的參數估計方法進行入水點精度評估，僅僅利用定型階段的試驗信息，要得到置信度較高的評判結果，需要較多的試驗樣本。不同于傳統的管裝發射魚雷，火箭助飛魚雷試驗屬于破壞性試驗，魚雷不能回收使用，這會造成試驗消耗大且組織、指揮和協調難度高，因而參數估計只能在小子樣條件下進行。由于火箭助飛魚雷在研制過程中，經歷方案設計驗證試驗、科研試驗等階段，Bayes 點估計方法可利用這些階段的入水點信息作為驗前信息確定驗前分布，并根據定型試驗時獲取的觀測數據進行參數估計，在同樣置信條件下，能降低試驗所需魚雷的條次數，從而有效地降低試驗消耗、縮短試驗周期、提高試驗效率［3］。基于此，本文利用Bayes 點估計方法［4］對火箭助飛魚雷入水點精度進行評定，僅利用較少的試驗條次數，就能以較高的置信度，實現入水點精度的評定。最后，給出了相容性檢驗的計算方法，并通過應用實例對所提方法進行了驗證。

1 Bayes 參數估計方法

Bayes 估計方法將魚雷入水點位置看作服從正態分布的隨機變量，將入水點偏差看作正態分布中的分布參數θ，并用概率分布函數描述參數θ 的未知狀況。

首先，由驗前信息確定驗前分布π(θ)，由現場試驗信息X={X1，X2，…，Xn}確定似然函數L(X|θ)，然后，利用Bayes公式綜合現場試驗信息和先驗信息，形成較完備的后驗分布在后驗分布的基礎上進行統計推斷，就能夠確定入水點精度的大小。

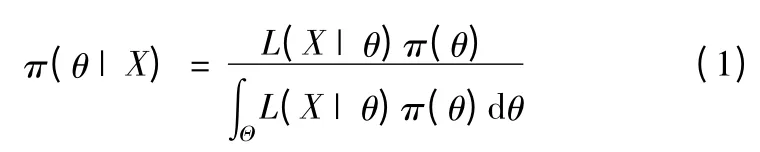
Bayes 方法在使用驗前信息時要求信息以分布函數的形式表示，而指標評定過程中這些信息一般以歷史數據、主觀信息或者經驗信息的形式存在，這就需要確定先驗分布函數的形式并計算相應的參數。選取恰當的先驗分布是正確反映先驗信息并進行統計推斷的前提和基礎，目前選取先驗分布的方法主要有共軛分步法、不變先驗分布法等，在滿足合理性要求的前提下，選取共軛分布能給估計帶來極大的方便，在此選取共軛先驗分布法進行研究。

1.1 分布假定［5］

對入水點精度指標σ，設D =σ2的驗前概率密度函數π(D)為逆Gamma 分布IGa(α0，β0)，即:

以雷達所在位置為原點，在縱平面上，目標位置信息主要由觀測距離r以及俯仰角θ來表征，其中觀測距離標準差為σr，俯仰角標準差為σθ，則對應的協方差矩陣為

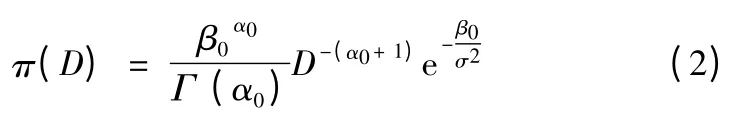
其中α0和β0是驗前概率密度函數中的兩個未知的分布參數，需要利用各種驗前信息確定其取值。Γ(·)表示Gamma函數。

1.2 驗前分布中超參數的計算

設定型試驗之前，在以理論入水點為坐標原點的發射坐標系下，有m 個驗前入水點信息{(Δx0i，Δz0i)|i =1，2，…，m}，其中(Δx，Δz)表示實際入水點相對于理論入水點的偏差。如果假定入水點偏差Δx ～N(0，D))，Δz ～N(0，D))，且Δx、Δz 相互獨立，令

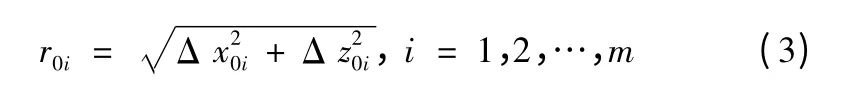
則r0i服從Rayleigh 分布，其概率密度函數:

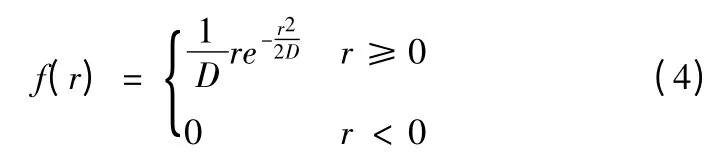
利用驗前信息{r0i|i=1，2，…，m}，根據Bootstrap 方法［6］求出D 的驗前均值和驗前方差。在計算機上，該過程可利用Monte Carlo 方法按以下步驟實現:

1)以R1，R2，…，Rn的實現(r1，r2，…，rn)為有限總體，進行有放回地簡單隨機抽樣，得到Bootstrap 觀察值(，…)，并由此構造隨機變量D 的一階矩=R，…，;Fn)和二階矩=R，…;Fn)。

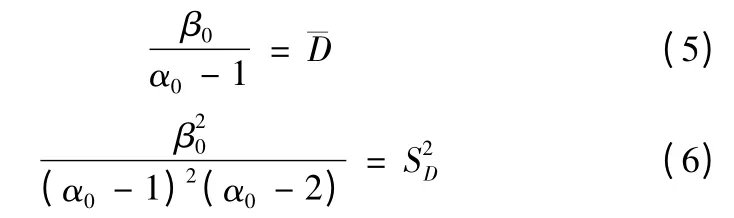
計算得到隨機變量D 驗前概率密度函數IGa(α0，β0)中的超參數α0和β0。

1.3 驗后概率密度函數的計算

如果定型試驗中測量得到的n 個入水點信息為X ={(Δxi，Δzi)|i=1，2，…，n}。同樣計算:

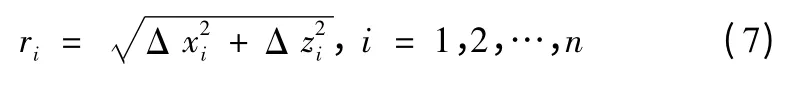
其中

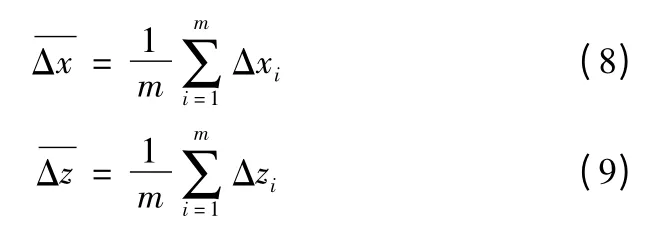
則似然函數為Rayleigh 分布函數的積:

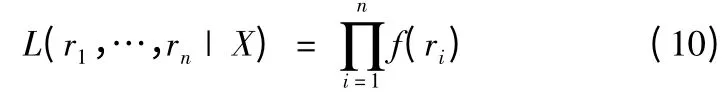
根據Bayes 理論，隨機變量D 的驗后概率密度函數可以表示如下:

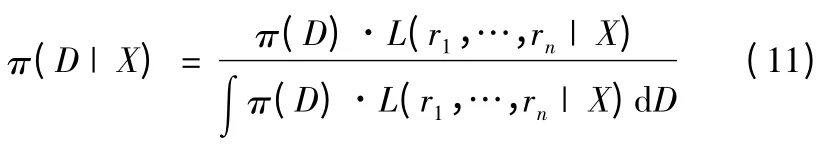
由于

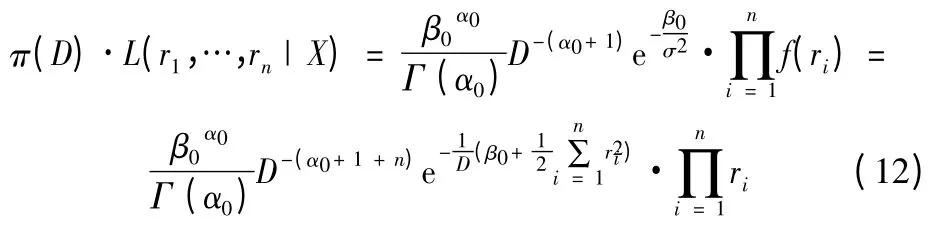
則

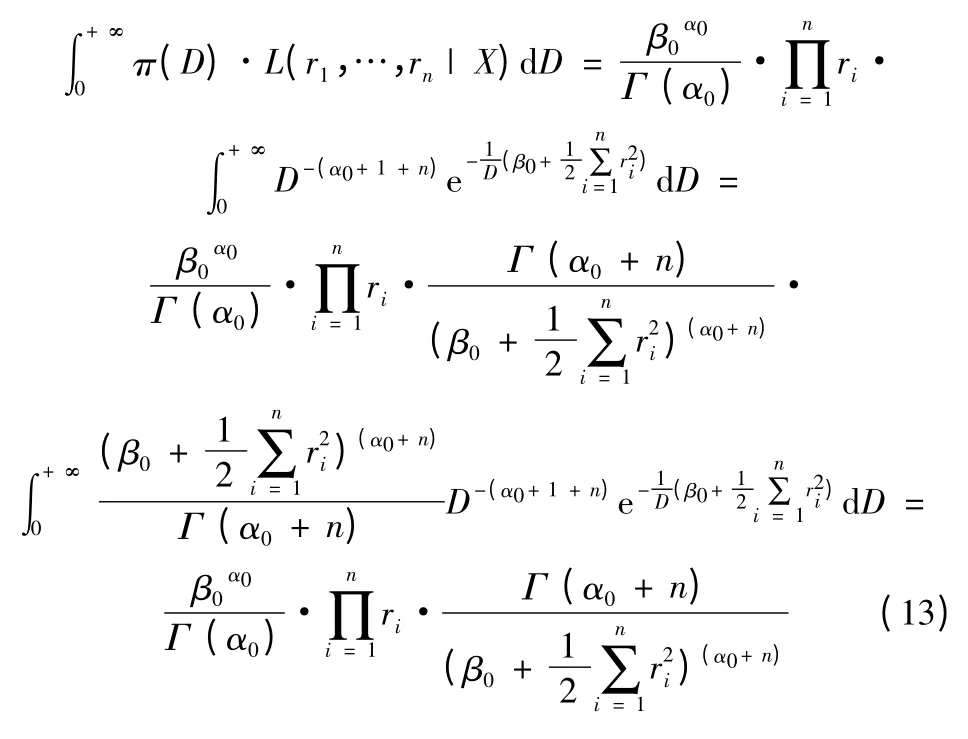
則D 的驗后概率密度函數:

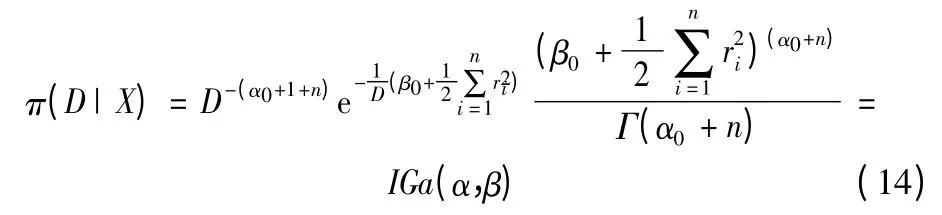
其中

由于D=σ2，可求得標準差σ 的驗后概率密度函數

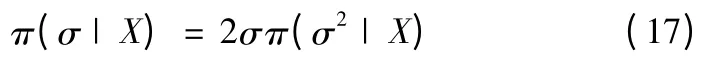
1.4 入水點精度估計

在均方誤差最小意義下，利用式(12)得到入水點精度的貝葉斯點估計值

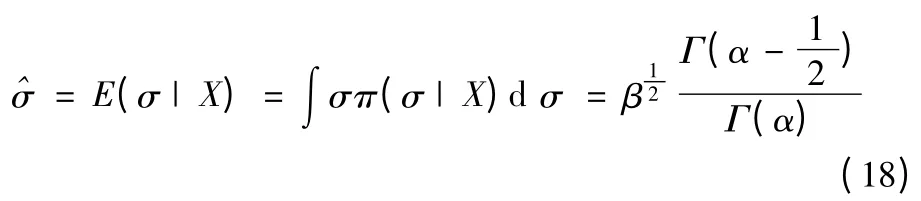
2 相容性檢驗

定型試驗之前的驗前數據是一種最常見的驗前信息形式，當對驗前數據直接運用Bayes 公式，實際上它是將驗前數據與試驗數據同等看待。此時，若兩者不相容，將會降低評判結果的置信度，因此需要進行相容性檢驗，以確定驗前信息是否可用。

相容性檢驗主要有Smirnov 檢驗、Wilcoxon 檢驗和Mood檢驗等方法。本文采用F 檢驗方法［7］確定驗前信息與現場信息的相容性。

設x1，x2，…，xn1為驗前信息中的一組入水點偏差，y1，y2，…，yn2為現場試驗中的一組入水點偏差。作統計量:

對于給定的顯著性水平α'，接受H'0假設的標準為P(F∈DA|H'0)=1-α'。即當F∈DA時，接受H'0，當F?DA時，拒絕H'0，接受H'1。DA為檢驗的臨界區域。對于F 檢驗，接收區域:

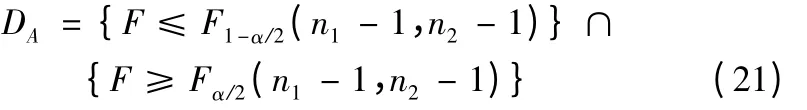
3 應用舉例

假定入水點精度指標規定不大于190 m。在以理論入水點為坐標原點的發射坐標系下，驗前入水點信息為{(256.76 m，12.57 m)，(366.29 m，342.25 m)，(-55.32 m，245.92 m)，(314.95 m，-145.14 m)}，由式(5)、(6)可計算出驗前超參數α0=2. 712、β0=3192. 5。現場試驗入水點信息為{(200.28 m，54.04 m)，(-289.50 m，-55.91 m)，(-97.50 m，- 193. 29 m)，(- 133. 43 m，289. 69 m)，(91. 52 m，-394.62 m)，(-24.64 m，-263.67 m)}，首先根據由式(21)，兩組數據是相容的，再由式(15)、(16)求得驗后超參數α=8.712、β=259 599。最后，根據式(18)得到入水點精度估計值為^σ=180.52 m。由于^σ≤190 m，入水點精度滿足指標要求。

4 結束語

為了解決火箭助飛魚雷系統復雜，試驗子樣數少，指標評定困難的問題，本文采用Bayes 點估計方法，融合各種驗前信息對入水點精度進行評定。首先對驗前信息與試驗現場信息的相容性進行檢驗，以確定驗前信息是否可用;然后利用兩種信息分別計算驗前和驗后概率密度函數，進而確定入水點精度的概率統計結果，判定該項指標是否滿足技術要求。最后通過應用實例驗證了本文方法的有效性。

［1］程光顯，張士峰.導彈落點精度的鑒定方法—概率圓方法［J］.國防科技大學學報，2001，23（5）:40-43.

［2］Kay S.Fundamentals of Statistical Signal Process，Estimation Theory［M］.Englewood Cliffs，NJ:Prentice-Hall，1993.

［3］王國玉，申緒澗.電子系統小子樣試驗理論方法［M］.北京:國防工業出版社，2003.

［4］GJB 6289—2008，地地彈道式導彈命中精度評定方法［S］.

［5］張金槐，唐雪梅.Bayes 方法（修訂版）［M］.長沙:國防科技大學出版社，1993.

［6］Efron B. Bootstrap methods: another look at the jackknife［J］.Annals of Statistics，1979，7（1）:1-26.

［7］張湘平.小子樣統計推斷與融合理論在武器系統評估中的應用研究［D］.長沙:國防科技大學，2003.

［8］馬錦垠，侯寶娥.火箭助飛魚雷入水點測量系統的設計與實現［J］.火力與指揮控制，2012（8）:199-201.