基于半參數回歸模型的最小一乘局部線性算法

蘇正軍,劉迎照

(洛陽師范學院數學科學學院,河南洛陽 471022)

基于半參數回歸模型的最小一乘局部線性算法

蘇正軍,劉迎照

(洛陽師范學院數學科學學院,河南洛陽 471022)

根據最小一乘準則,推導出最小一乘局部線性估計的計算方法,并通過對模擬數據的計算和分析,對比最小一乘核算法和最小二乘局部線性算法,驗證了最小一乘局部線性算法是一種有效的,穩健的估計方法,并且有降低邊界效應的作用.

半參數回歸模型;最小一乘;局部線性估計;算法;穩健性

1 引言

考慮半參數回歸模型[1]:

其中,Xi是p維隨機變量,β為p維待估參數,g(·)為R1上未知的Borel函數,{ui}是獨立同分布的隨機誤差序列,且E(ui)=0,0＜＜∞.半參數回歸模型的估計問題就是基于(Yi,Xi,Ti)估計β和g.

目前,對于半參數回歸模型的估計算法有兩種思路:一種是對非參數部分加以光滑限制,使用合理的參數逼近,即將非參數部分參數化;另外一種是分別對參數和非參數部分進行估計的兩階段估計方法.可以先假定參數已知,使用標準的非參數方法估計非參數部分,然后去掉非參數部分,再使用標準的參數方法估計參數部分.

對于參數部分的估計,多數估計方法選擇最小二乘準則,如最小二乘核估計,最小二乘k近鄰估計,最小二乘局部線性估計等.但是最小二乘估計受異常點的影響較大,而最小一乘準則要小很多,最小一乘準則的穩健性比最小二乘準則好[2],在經常出現異常值的現實數據處理上,使用最小一乘準則擬合效果會更好一些.

本文將基于最小一乘準則的局部線性擬合的方法應用于半參數回歸模型.對非參數部分進行局部線性擬合,對線性部分采用最小一乘估計.通過對模擬數據的計算和分析,將此方法的擬合效果與最小一乘核算法和最小二乘局部線性算法作對比,驗證最小一乘局部線性算法的有效性和穩健性.

2 基本原理和方法

2.1 最小一乘

最小二乘估計得到廣泛應用的一個重要原因是計算簡單,它的極小值求解可以通過簡單的公式表達出來.而最小一乘估計的極值求解是不可微的優化問題,計算復雜.文獻[2]分情況討論了最小一乘估計的算法,文獻[3]研究了基于模擬退火算法的最小一乘回歸算法,這些都為我們通過M atlab軟件計算最小一乘估計提供了可能.因此,在本文中采取最小一乘估計方法對參數部分進行估計.

2.2 局部多項式估計

雖然核估計算法實現了局部加權,但是權重在局部鄰域內是常量,由于加權是基于整個樣本點的,所以在邊界處的估計往往不理想.常用的解決方法是用一個變動的函數取代局部固定的權重.就是在待估點t的鄰域內用一個線性函數g(Ti)=a+bTi,Ti∈[t-hn,t+hn]取代g(Ti)的平均,其中a和b是兩個局部參數,進而得到了局部線性估計算法.

在內點,使?g(t,hn)的均方誤差達到最小的最優核函數是:K(t)=0.75(1-t2)+,此時局部線性估計的收斂速度O(n-2/5)(見文獻[4]).局部線性估計避免了通常核估計的邊界效應問題.并且已被證明無論在邊界點還是內點都是最佳線性估計[5],因此,在本文中采取局部線性回歸方法對非參數部分進行估計.

2.3 最小一乘局部線性算法

3 模擬驗證

可見參數β=1,非參數部分g(t)=1+cos(8t+5),圖1為g(t)的真實曲線圖.

選擇Enanechnikov(拋物核)K(u)=0.75(1-u2)+,這是因為它是在內點,使得均方誤差達到最小的最優核函數.

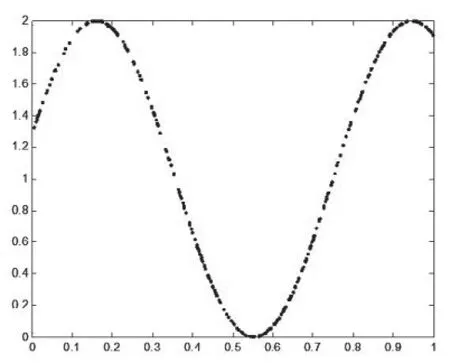
圖1 (8)式中的g(t)真實曲線圖

3.1 窗寬選取對擬合效果的影響

窗寬可以反映光滑程度,降低擬和曲線在峰頂區域的偏差以及尾部區域的方差,提高擬合曲線的靈活性[7].使得均方誤差達到最小的最佳窗寬為hn=,其中c與n無關,只與回歸函數,解釋變量的密度函數和核函數有關[4].關于最優窗寬的選取,一般的方法是由對漸近加權積分均方誤差W ISE極小化而得到.窗寬的選取問題,在文獻[5]中有詳細的討論,在本文中不對此問題加以研究,只是將最小一乘局部線性擬合方法與變窗寬思想結合,所得估計繼承了二者的優點,hn初始窗寬的理論值最優窗寬可以通過交錯鑒定法獲得[6].

使用交錯鑒定法確定的最優窗寬近似為hn=(n=300),在此選取c=0. 1;c=0. 3; c=0.9,通過模擬數據,分析窗寬的選取對擬合效果的影響.分別采用最小一乘準則和最小二乘準則分別進行5次模擬,并比較β?和真實β=1的平均絕對誤差.結果如表1:通過表1數據可以看出,隨著c的增大,β?的平均絕對偏差也增大,說明窗寬越大,擬合誤差越大.

當c=0.1時,窗寬過小,標準差雖小,但是擬合曲線缺乏光滑性,是沒有意義的估計,擬合效果圖見圖2a;當c=0.9時,窗寬過大,擬合曲線雖然光滑,但是卻以增大標準差為代價,擬合效果變差,擬合效果圖見圖2b.由此可見,在半參數線性回歸模型中窗寬的變化不但影響β的估計精度,而且影響曲線的擬合精度,所以選擇最優窗寬是必須的.

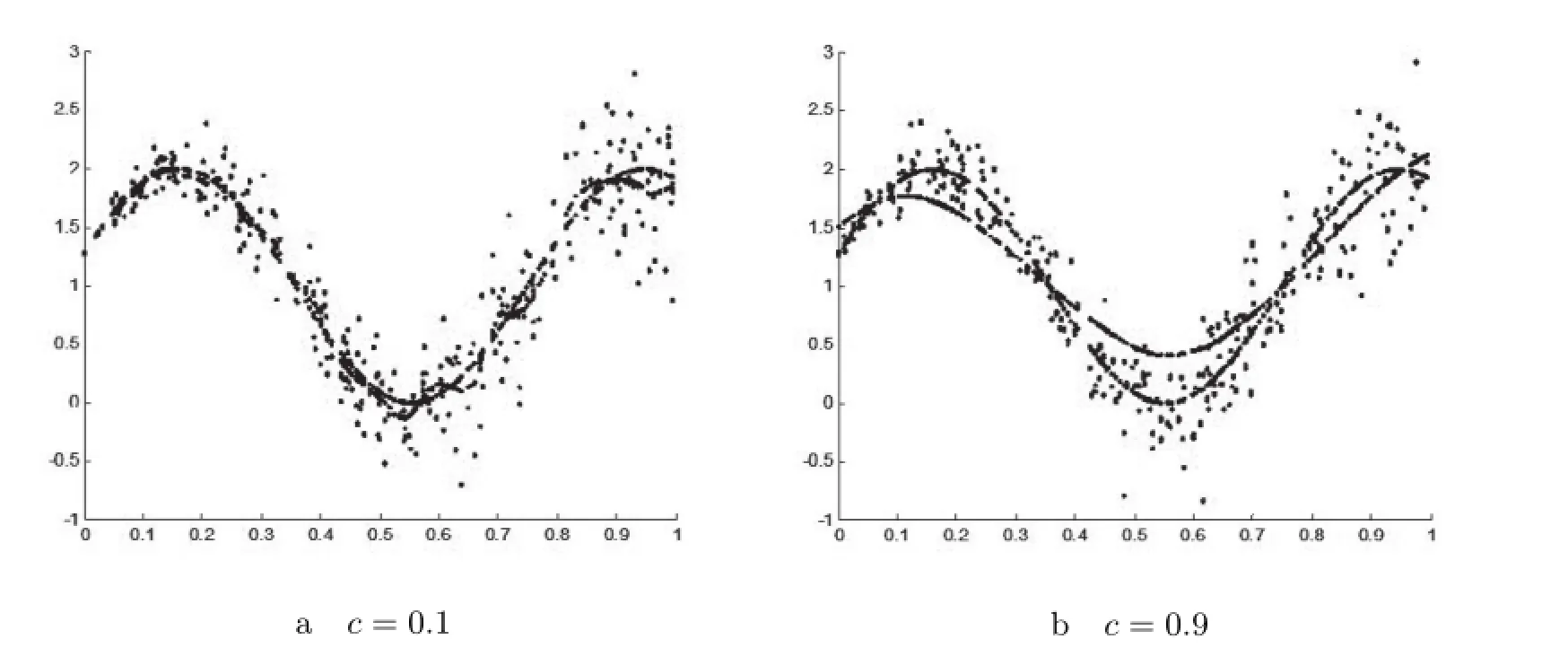
圖2 窗寬過小和窗寬過大的擬合效果圖,(T,Y-Xβ)的散點圖和g(t)擬合曲線

當c=0.3,不論采用最小一乘局部線性估計,還是最小二乘局部線性估計,估計值與真實值的平均絕對誤差都很小,估計效果都很理想,可見最小一乘局部線性估計是一種對半參數回歸模型有效的估計方法.擬合效果見圖3.

3.2 降低邊界效應

對比最小一乘局部線性算法和最小一乘核算法[8-9]的擬合圖,驗證最小一乘局部線性算法有效的降低了邊界效應.最小一乘核算法的擬合曲線左邊和右邊的邊界點處有高估的現象(見圖4),g(t)曲線的真實走向(見圖1)有很大的線性傾斜,最小一乘局部線性估計很好的擬合出了這一趨勢,有效的降低了邊界效應.

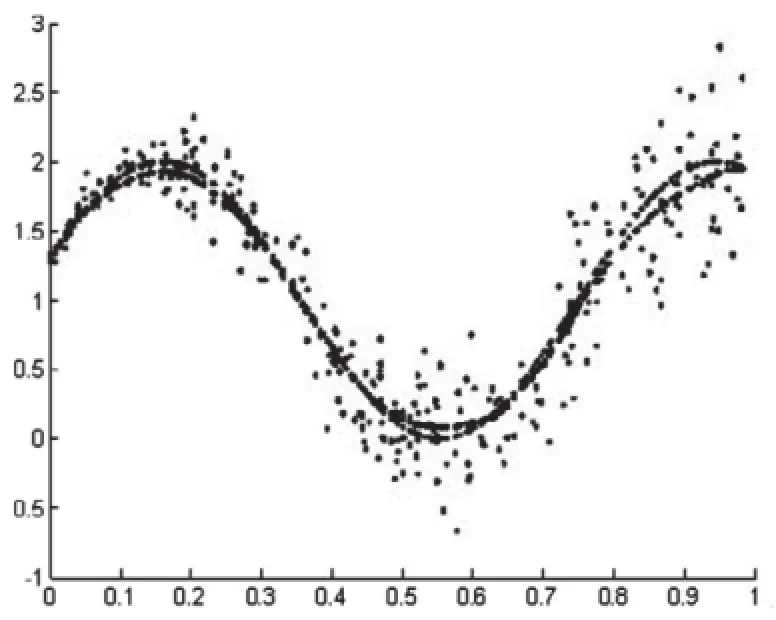
圖3 c=0.3時,最小一乘局部線性估計和最小二乘局部線性估計擬合效果圖

圖4 最小一乘局部線性估計和最小一乘核估計擬合圖,(T,Y-Xβ)的散點圖和g(t)擬合曲線

3.3 最小一乘局部線性算法的穩健性

分別從伸縮和平移兩種情況,引入兩個異常值y1=10y1和y2=y2+5,當c=0.3時對數據進行5次模擬,并比較?β和真實β=1的平均絕對誤差.結果如表2:

表2 引入異常值前后,5次模擬結果

由上表可以看出,在引進異常值之前,最小二乘局部線性算法和最小一乘局部線性算法的平均絕對誤差都很小,引進異常值后,兩種估計方法的平均絕對誤差都有增加,但是最小一乘局部線性算法的增加值僅為0.000 32,最小二乘局部線性算法平均絕對誤差增加值為0.026 38,引入異常值前后最小二乘局部線性算法的估計偏差比最小一乘局部線性算法的估計偏差大,由此說明最小一乘局部線性算法的穩健性.

引進異常值前最小一乘局部線性算法與最小二乘局部線性算法的擬合圖見圖5a,它們擬合曲線基本重合,與g(t)的真實曲線(見圖1)走勢趨向非常相近,進一步驗證了最小一乘局部線性算法的有效性.引進異常值后最小一乘局部線性算法與最小二乘局部線性算法的擬合圖見圖5b,由圖5可以看出,最小二乘局部線性算法擬合曲線變化較大,而最小一乘局部線性算法擬合曲線變化相對很小,從而進一步驗證了最小一乘局部線性算法對異常值處理的穩健性.

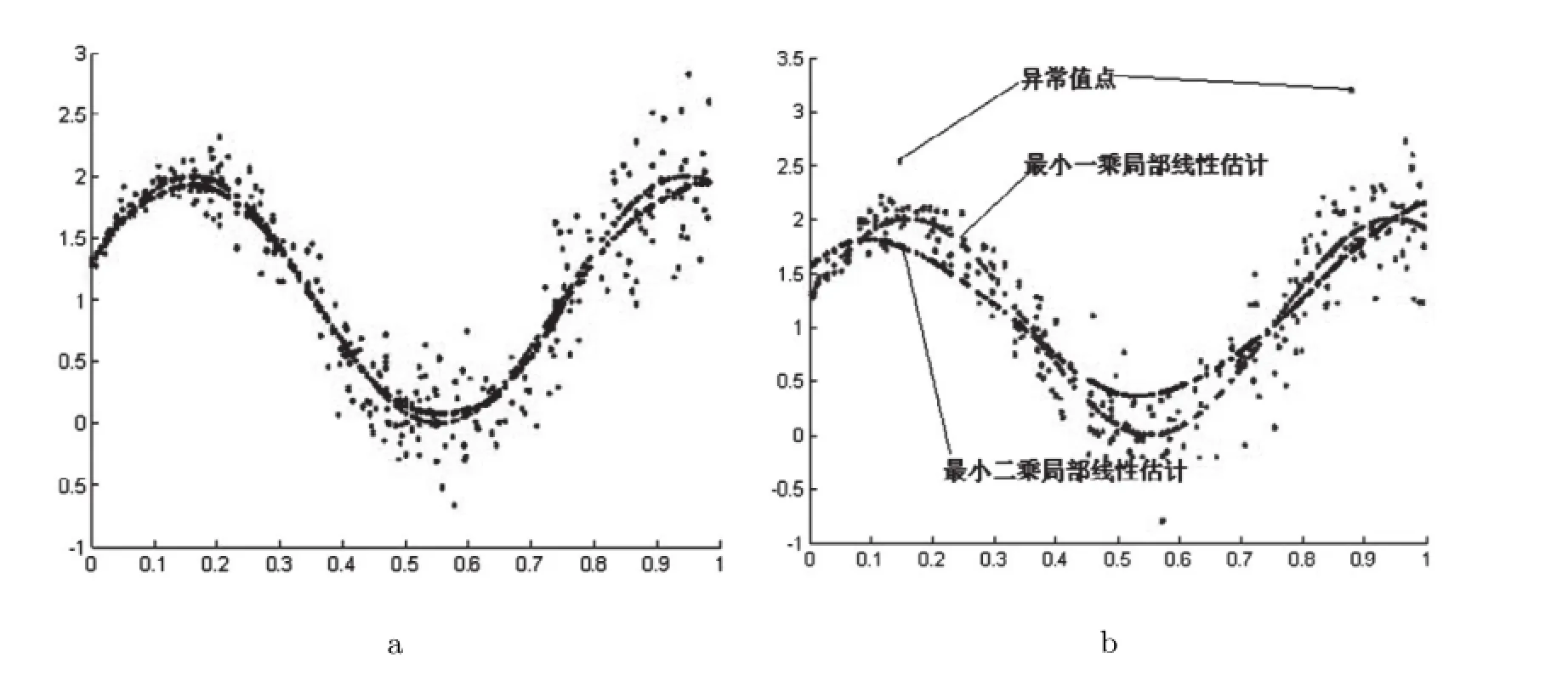
圖5 引進異常值前后,最小二乘局部線性估計和最小一乘局部線性估計擬合圖, (T,Y-Xβ)的散點圖和g(t)擬合曲線

4 結束語

本文提出的半參數回歸模型的最小一乘局部線性算法,經模擬數據驗證其在模型擬合上非常理想;通過與最小一乘核算法比較,驗證了最小一乘局部線性估計在降低邊界效應的優勢;通過對異常數據的分析,驗證了最小一乘局部線性算法比最小二乘局部線性算法表現的更加穩健.

[1]柴根象,孫平,蔣澤云.半參數回歸模型的二階段估計[J].應用數學學報,1995,18(3):353-363

[2]陳希孺.最小一乘線性回歸(上)[J].數理統計與管理,1989(5):48-55.

[3]王福昌,張寶雷,曹慧榮.基于模擬退火算法的最小一乘回歸新算法[J].數理統計與管理,2008,27(6):1047-1052.

[4]王星.非參數統計[M].北京:清華大學出版社,2009.

[5]Fan J,Gijbels I.Local Polonom inal Modeling and Its App lications[M].London:Chapman and Hall,1996.

[6]樊明智,王芬玲,郭輝.縱向數據半參數回歸模型的最小二乘局部線性估計[J].數理統計與管理,2006,25(2): 170-174.

[7]葉阿忠.非參數計量經濟學[M].天津:南開大學出版社,2003.

[8]呂書龍,劉文麗.最小一乘估計快速算法[J].應用概率統計,2008,24(6):621-630.

[9]呂書龍,梁飛豹,劉文麗.半參數線性回歸模型的最小一乘核估計[J].福州大學學報,2011,39(2):187-191.

Least abso lu te dev iation local linear a lgorithm based on sem iparam eteric regression m odel

Su Zhengjun,Liu Yingzhao

(School of M athematics Science,Luoyang Normal University,Luoyang 471022,China)

Based on the least absolute deviation estimation,local linear least absolute deviation algorithm is derived.The ef ectiveness and robustness of our method are verif ed by simu lation com pared w ith the least absolute deviation kernel algorithm and local linear least squares algorithm.Themodel can also reduce the boundary ef ect.

sem iparam etric regression m odel,least absolute deviation,local linear estim ation, algorithm,robustness

O242.1

A

1008-5513(2013)05-0513-07 DO I：10.3969/j.issn.1008-5513.2013.05.011

2013-06-01.

河南省基礎與前沿技術研究計劃項目(102300410216).

蘇正軍(1954-),講師,研究方向：基礎數學及應用.

2010 MSC:03C65